Nerovnice o s to nerovnice Rieenie kvadratickej a

Nerovnice ¬ Čo sú to nerovnice ¬ Riešenie kvadratickej a bikvadratickej nerovnice ¬ Riešenie lineárnych nerovníc Marek Balušík 2010/2011 3. B Koniec

Ø Nerovnice sú tvorené dvoma matemaickými výrazmi, ktoré sú spojené znakmi: <, >, ≤ alebo ≥. Ø Nerovnica je algebraická úloha, pri ktorej sa hľadajú všetky čísla danej množiny, ktoré spĺňajú danú nerovnosť. Ø Pri nerovniciach sa často používa grafické riešenie, pretože je názorné. Ø Riešiť nerovnosť znamená nájsť množinu všetkých jej riešení. Začiatok Späť Ďalej Koniec

¬ Ekvivalentné úpravy nerovníc: ¬ vzájomná výmena strán nerovnice so súčasnou zmenou znaku nerovnosti na obrátený; ¬ nahradenie ľubovoľnej strany nerovnice výrazom, ktorý sa jej rovná v celom obore riešenia nerovnice, pričom znak nerovnosti sa nezmení; ¬ pripočítaním toho istého čísla alebo výrazu s neznámou, ktorý je definovaný v celom obore riešenia, k obom stranám nerovnice, pričom znak nerovnosti sa nemení; ¬ vynásobenie oboch strán nerovnice kladným číslom alebo výrazom s neznámou, pričom znak nerovnosti sa nemení; ¬ vynásobenie oboch strán nerovnice záporným číslom nebo výrazom s neznámou, pritom znak nerovnosti sa zmení v obrátený; ¬ umocnenie oboch strán nerovnice prirodzeným mocniteľom, ak sú obe strany nerovnice nezáporné, pritom znak nerovnosti sa nemení; ¬ odmocnenie oboch strán nerovnice prirodzeným odmocniteľom, ak sú obe strany nerovnice nezáporné, pričom znak nerovnosti sa nemení; ¬ zlogaritmovaní oboch strán nerovnice pri tom istom základe väčšom ako 1, ak sú obe strany nerovnice kladné, pritom znak nerovnosti sa nemení. Začiatok Späť Ďalej Koniec

Riešenie kvadratickej Majme nerovnicu: 3 x 2 – 7 x + 4 ≤ 0 V prvom rade si zistíme korene kvadratickej rovnice 3 x 2 – 7 x + 4 = 0. Dostávame: x 1 = 1 a x 2 = 4/3 Z týchto koreňov dostaneme nerovnicu 3*(x – 1)*(x – 4/3) ≤ 0 Z prvej časti dostávame riešenie x 1 <1, 4/3>. Riešením druhej časti je prázdna množina. Zjednotením týchto dvoch intervalov dostávame riešenie tejto nerovnice a je to: x <1, 4/3>. Začiatok Späť Ďalej Koniec

tabuľka Korene vyššie uvedenej rovnice nám rozdelia interval riešenia na tri časti, t. j. : 1. x (- ∞ , 1), 2. x (1, 4/3) a 3. x (4/3, ∞ ) - 7 x +4 > 0 Začiatok (- , 1) (1, 4/3) (4/3, ) 4 -0, 07 234 + - + Späť Ďalej Koniec

Bikvadratická nerovnica x 4 – 5 x 2 + 4 < 0 Metóda nulových bodov: Koreňmi tejto rovnice sú čísla -2; -1; 1; 2. Tieto nám rozdelia interval na 5 častí: 1. 2. x (- ∞, - 2), 2. x (-2, - 1), 3. x (- 1, 1), 4. x (1, 2) a 5. x (2, ∞) Z jednotlivých intervalov boli vybrané čísla (postupne ako idú intervaly) -3; -1. 5; 0; 1. 5; 3. Riešenie je zobrazené v tabuľke: Začiatok (-∞ , -2) (-2, -1) (-1, 1) (1, 2) (2, ∞ ) 40 -2, 19 40 + - + Späť Ďalej Koniec

Sústava lineárnych nerovníc s jednou neznámou 5 x – 3 ≤ 3 x + 1 < 5 x Rozdelíme si nerovnicu na dve časti a riešíme samostatne: 5 x – 3 ≤ 3 x + 1 < 5 x 2 x ≤ 4 1 < 2 x x≤ 2 x>½ ¬ Výsledné rišenie dostávame prienikom čiastkových riešení (intervalov). To si zakreslíme graficky: ¬ Riešením je žlto vyšráfovaná plocha, a teda: x (1/2 , 2> Začiatok Späť Koniec

Lineárne nerovnice s jednou neznámou a metóda nulových bodov Majme nerovnicu: (2 x – 3) / (3 x – 7) > 0 Ako prvú vec, ktorú pri riešení nerovníc spravíme je to, že zistíme D(f) nerovnice. 2 x – 3 > 0 a 3 x – 7 > 0 2 x – 3 < 0 a 3 x – 7 < 0 x > 3/2, x > 7/3 x < 3/2, x < 7/3 x 1 (7/3, ) x 2 (- , 3/2) Výsledný hľadaný interval dostávame spojením čiastkových intervalov. Teda: x = x 1 x 2 = (-∞ , 3/2) (7/3, ∞ ) Tento istý príklad si teraz vyriešime metódou nulových bodov: 1. Celú nerovnicu si upravíme do takého tvaru, aby na jej pravej strane bola nula, tzn. všetko, čo je na pravej strane úpravami prehodíme na stranu ľavú (naša nerovnica je už do takéhoto tvaru upravená, preto to robiť nemusíme) 2. Prirovnáme menovateľa aj čitateľa k nule a vyriešime: 2 x – 3 = 0 → x = 3/2 3 x – 7 = 0 → x = 7/3 Začiatok Späť Koniec

3. Toto riešenie nám celý interval rozdelí na podintervaly: 1. (- , 3/2), 2. (3/2, 7/3) a 3. (7/3, ) 4. Pre každý jeden interval určíme, či je menovateľ a čitateľ kladný alebo záporný. To spravíme tak, že si vyberieme nejakú hodnotu z daného intervalu a dosadíme do nerovnice, napríklad z prvého intervalu si vezmem „-1“ 2*(-1) – 3 = -5 3*(-1) – 7 = -10 5. Riešenia si prehľadnosť zapíšeme do tabuľky: (-∞ , 3/2) (3/2, 7/3) Začiatok (7/3, ∞ ) 2 x - 3 - + + 3 x - 7 - - + Späť Koniec

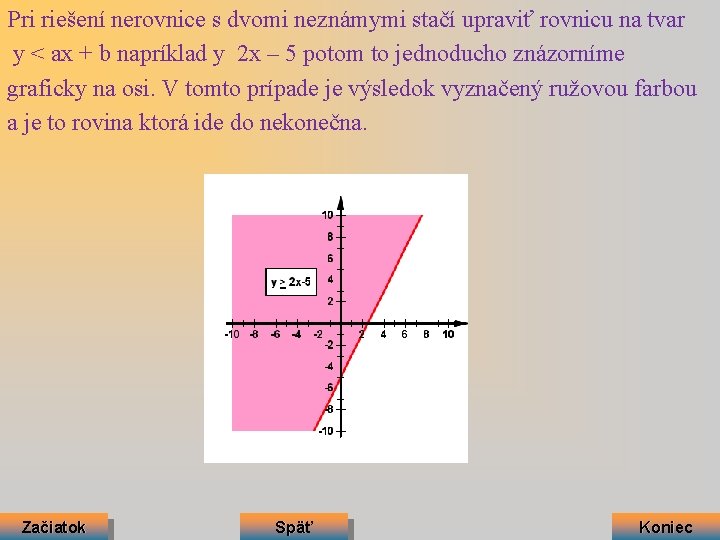
Pri riešení nerovnice s dvomi neznámymi stačí upraviť rovnicu na tvar y < ax + b napríklad y 2 x – 5 potom to jednoducho znázorníme graficky na osi. V tomto prípade je výsledok vyznačený ružovou farbou a je to rovina ktorá ide do nekonečna. Začiatok Späť Koniec

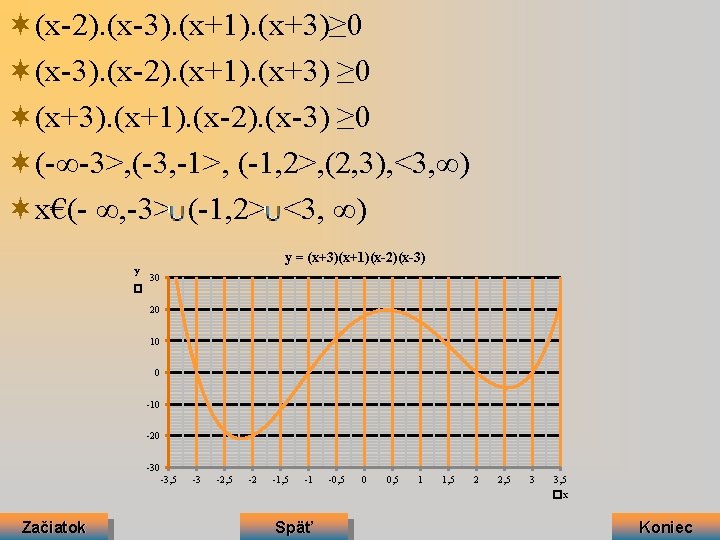
• Riešenie nerovnice s 1 neznámou túto nerovnosť riešime takou istou metódou ako kebz sme riešili rovnicu 4. stupňa : Po dosadzovaní získame 1 koreň rovnice x 1=2 Týmto sa nám podarilo znížiť stupeň rovnice o 1 dostali sme kubickú rovnicu: =0 Druhý koreň je: x 2=3 ): (x-3)= = Začiatok +4 x+3 =x 3= -1 x 4= -3 Späť Ďalej Koniec

Ďakujem za pozornosť 13