Murd ja juurvrrand T Lepikult 2004 Murdvrrandi definitsioon

Murd- ja juurvõrrand © T. Lepikult, 2004

Murdvõrrandi definitsioon Murdvõrrandiks nimetatakse võrrandit, milles muutuja esineb murru nimetajas. Murdvõrrandit saab samasusteisenduste abil teisendada kujule Murdvõrrandi lahendamiseks lahendatakse võrrand mis on esialgse võrrandi järeldus (lahendite arv võib olla kasvanud). Et muutuja x lubatavad väärtused on kitsendatud tingimusega siis tuleb lahendamisel alati kontrollida, kas saadud muutuja väärtused on esialgse võrrandi lahendeiks või mitte. algusesse eelmine slaid järgmine slaid esitluse lõpp

Murdvõrrandi lahendamine Näide Lahendada võrrand Lahendus Viime vasakul pool võrdusmärki olevad avaldised ühisele murrujoonele: Saadud ruutvõrrandi lahendid on: Neist on esialgse võrrandi lahend, (nimetaja on x = 3 korral null). on aga võõrlahend Vastus. Võrrandi lahendiks on x = – 2. algusesse eelmine slaid järgmine slaid esitluse lõpp

Juurvõrrandi definitsioon ja lahendamine Juurvõrrandiks nimetatakse võrrandit, milles muutuja esineb juuritavas. Näited Võrrandid võrrand on juurvõrrandid, kuid ei ole juurvõrrand. Juurvõrrandi lahendamiseks astendatakse enne sobivalt teisendatud võrrandi mõlemat poolt ühe ja sama astendajaga. Lahendamisel saadud muutuja väärtusi tuleb tingimata esialgse võrrandi abil kontrollida, sest võrrandi mõlema poole astendamisel paarisarvuga on võimalus võõrlahendite tekkimiseks. algusesse eelmine slaid järgmine slaid esitluse lõpp

Näiteid juurvõrrandi lahendamisest Näide 1 (1) Lahendame võrrandi Lahendus Kuna (vt. juure omadusi, 5. omadus), siis on lahendatav võrrand samaväärne võrrandiga mille lahendid on arvu absoluutväärtuse definitsiooni kohaselt ja Kontrollimisel selgub, et mõlemad lahendid (x = 3 ja x = -3) sobivad. Vastus. Võrrandi lahendid on algusesse ja eelmine slaid järgmine slaid esitluse lõpp

Näiteid juurvõrrandi lahendamisest Näide 2 (2) Lahendame võrrandi Lahendus Viime kõik liikmed peale juure võrrandi paremale poolele. Saame samaväärse võrrandi Tõstes viimase võrrandi mõlemad pooled ruutu, saame ruutvõrrandi: Kahe arvu vahe ruudu valemi põhjal asendame selle võrrandi parema poole hulkliikmega 16 – 8 x + x 2: algusesse eelmine slaid järgmine slaid esitluse lõpp

Näiteid juurvõrrandi lahendamisest (3) Näide 2 (järg) Saadud ruutvõrrandi kõik liikmed viime võrrandi vasakule poolele: koondame sarnased liikmed: ja korrutame viimatisaadud võrrandi mõlemad pooled arvuga – 1: Lahendame saadud ruutvõrrandi: algusesse eelmine slaid järgmine slaid esitluse lõpp

Näiteid juurvõrrandi lahendamisest (4) Näide 2 (järg) Kontrollime saadud “lahendikandidaate”, asetades nende väärtused tundmatu x asemele esialgses võrrandis 1) Lahendikandidaat x = 6 ei sobi, sest esialgse võrrandi vasak pool ei ole sel korral võrdne parema poolega. 2) Lahendikandidaat x = 3 sobib lahendiks, sest esialgse võrrandi vasak pool võrdub sel korral parema poolega. Vastus. Võrrandi lahend on algusesse eelmine slaid järgmine slaid esitluse lõpp

Näiteid juurvõrrandi lahendamisest Näide 3 (5) Lahendame võrrandi Lahendus Võrdusmärgist vasakule poole jätame esimese juuravaldise, ülejäänud liikmed viime vastandmärkidega võrrandi paremale poolele. Tulemusena saame samaväärse võrrandi Tõstame selle võrrandi mõlemad pooled ruutu: (1) Kuna , (vt. juure omadusi, 7. omadus), siis saame võrrandi (1) vasakul poolel : algusesse eelmine slaid järgmine slaid esitluse lõpp

Näiteid juurvõrrandi lahendamisest (6) Näide 3 (järg) Võrrandi (1) parema poole teisendamisel kasutame esmalt kahe arvu vahe ruudu valemit (valem (2) arvutamise abivalemitest): seetõttu Võrrandist (1) järeldub seega võrrand Selles võrrandis viime paremalt poolt võrdusmärki kõik liikmed peale juuravaldise vastandmärkidega vasakule ja koondame sarnased liikmed: algusesse eelmine slaid järgmine slaid esitluse lõpp

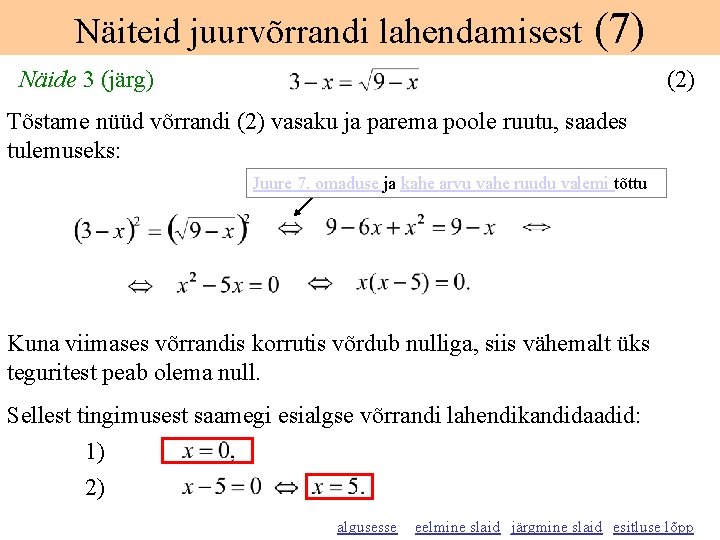
Näiteid juurvõrrandi lahendamisest (7) Näide 3 (järg) (2) Tõstame nüüd võrrandi (2) vasaku ja parema poole ruutu, saades tulemuseks: Juure 7. omaduse ja kahe arvu vahe ruudu valemi tõttu Kuna viimases võrrandis korrutis võrdub nulliga, siis vähemalt üks teguritest peab olema null. Sellest tingimusest saamegi esialgse võrrandi lahendikandidaadid: 1) 2) algusesse eelmine slaid järgmine slaid esitluse lõpp

Näiteid juurvõrrandi lahendamisest (8) Näide 3 (järg) Lahendikandidaatideks saime: 1) x = 0 ja 2) x = 5. Kontrollime saadud “lahendikandidaate”, asetades nende väärtused tundmatu x asemele esialgses võrrandis 1) (esimene lahendikandidaat sobib) 2) (teine lahendikandidaat ei sobi) Vastus. Võrrandi lahend on algusesse eelmine slaid esitluse lõpp