Ringjoon ring sektor T Lepikult 2004 Ringjoone vrrand

Ringjoon, ring, sektor © T. Lepikult, 2004

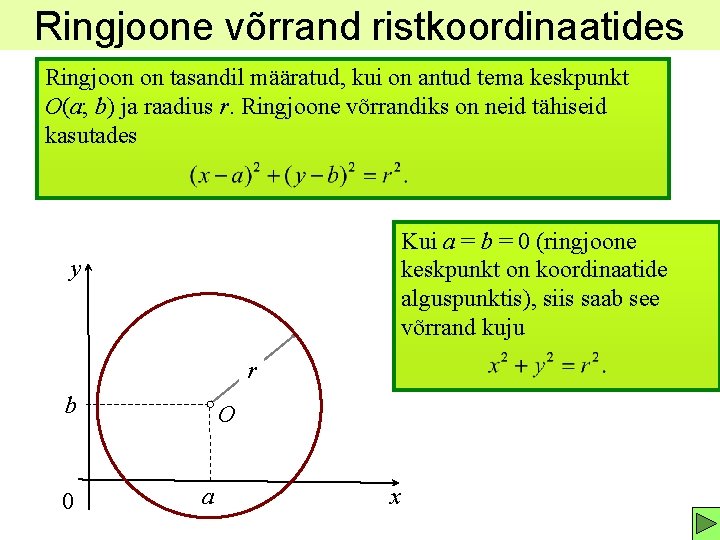
Ringjoone võrrand ristkoordinaatides Ringjoon on tasandil määratud, kui on antud tema keskpunkt O(a; b) ja raadius r. Ringjoone võrrandiks on neid tähiseid kasutades Kui a = b = 0 (ringjoone keskpunkt on koordinaatide alguspunktis), siis saab see võrrand kuju y r b 0 O a x

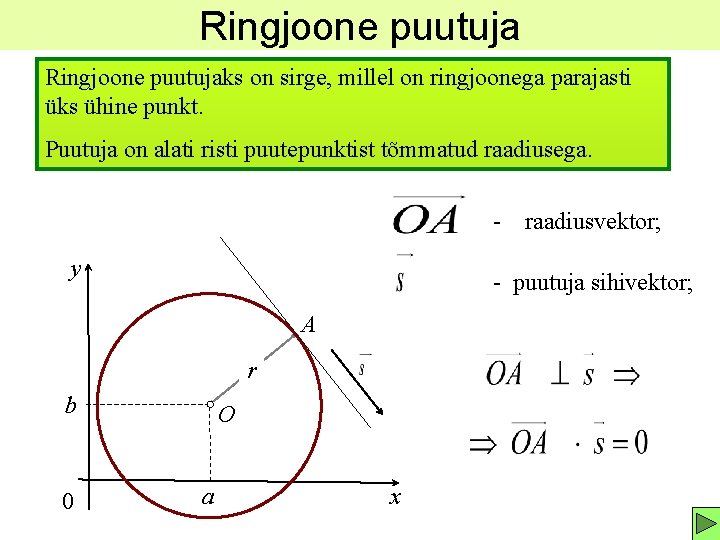
Ringjoone puutujaks on sirge, millel on ringjoonega parajasti üks ühine punkt. Puutuja on alati risti puutepunktist tõmmatud raadiusega. - raadiusvektor; y - puutuja sihivektor; A r b 0 O a x

Näide (I) Leida ringjoone x 2 + y 2 12 x + 2 y + 12 = 0 puutuja võrrand, kui puutepunktiks on punkt A(9; 3). Lahendus Ringjoone puutujalt on teada punkt A. Sirge võrrandi konstrueerimiseks on vaja veel teada sirge sihivektorit. Sihivektori leidmiseks kasutame seadust, et puutuja on risti puutepunktist tõmmatud raadiusvektoriga. Selleks aga, et määrata raadiusvektor, peame esmalt leidma ringjoone keskpunkti O. Keskpunkti leidmiseks teisendame ringjoone võrrandi kujule (x – a)2 + (y – b)2 = r 2.

Näide (II) Selleks eraldame võrrandi vasakul poolel täisruudud: millest näeme, et ringjoone keskpunkt on O(6; -1). Leiame nüüd raadiusvektori koordinaadid: Kuna raadiusvektor on risti sirge sihivektoriga nende vektorite skalaarkorrutis olema null: siis peab

Näide (III) Konstrueerime nüüd puutujaks oleva sirge võrrandi (teame, et sirgel asetseb punkt A(9; 3) ja et sirge sihivektoriks on s) : Viimasest seosest taandub välja suurus s 2 ning pärast lihtsustamist saame puutuja võrrandiks

Ringjoone pikkus ja ringi pindala Ringjoone pikkus c on leiatav valemiga kus r tähistab ringjoone raadiust, d diameetrit ja p irratsionaalarvu, mille lähisväärtusena kasutatakse praktilistes arvutustes arvu 3, 14. Samu tähiseid kasutades on ringi pindala S võimalik leida valemiga

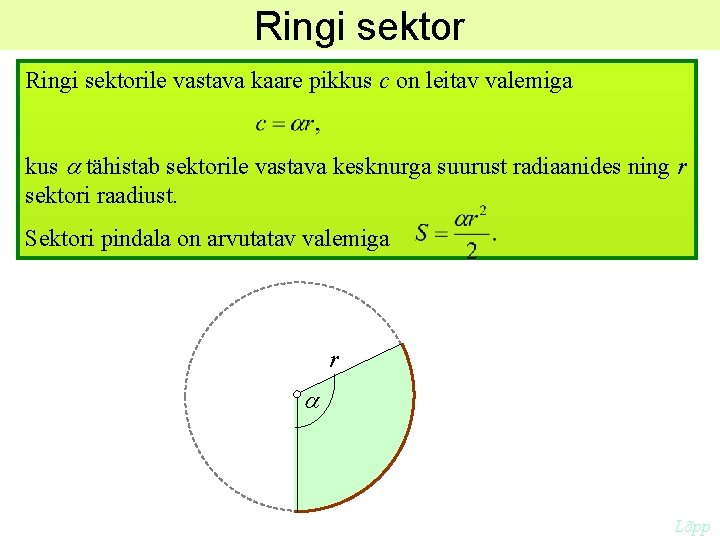
Ringi sektorile vastava kaare pikkus c on leitav valemiga kus a tähistab sektorile vastava kesknurga suurust radiaanides ning r sektori raadiust. Sektori pindala on arvutatav valemiga r a Lõpp