MultiDimensional Arrays Matrices Arrays seen so far are

Multi-Dimensional Arrays

Matrices • Arrays seen so far are single dimensional – A linear list of items – One subscript for accessing individual elements • Multidimensional arrays are useful organizations in many applications – values of temperatures at different locations in different times – number of runs in different sessions on different days in a test match – trajectory of a planet in space - time • Matrices – simplest and useful multidimensional arrays – Two dimensions

Two-Dimensional Data Structures • Fortran allows variables that can assume two dimensional array values • Typical values are: 23 14 9 5. 6 78. 9 23. 2 12 67 89 4. 7 0. 7 15. 2 9 5 56 6. 0 98. 2 76. 5 5. 2 23. 0 14. 6 . true. . false. . true. – An integer 3 by 3 matrix: 3 rows and 3 columns of integer values – 4 by 3 real matrix – 3 by 2 logical matrix

Matrix Declaration • Matrix entries can be of different types • No. of rows and columns can be arbitrary • Fortran Declaration defines these two attributes for a matrix variable – Real, Dimension(3, 6): : Sum – Logical, Dimension(23: 100, -2: 5): : flag – integer, Dimension(15: 19, 5): : runs • Accessing an element – Sum(2, 5), flag(56, 0), runs(18, 3) • Two subscripts are needed

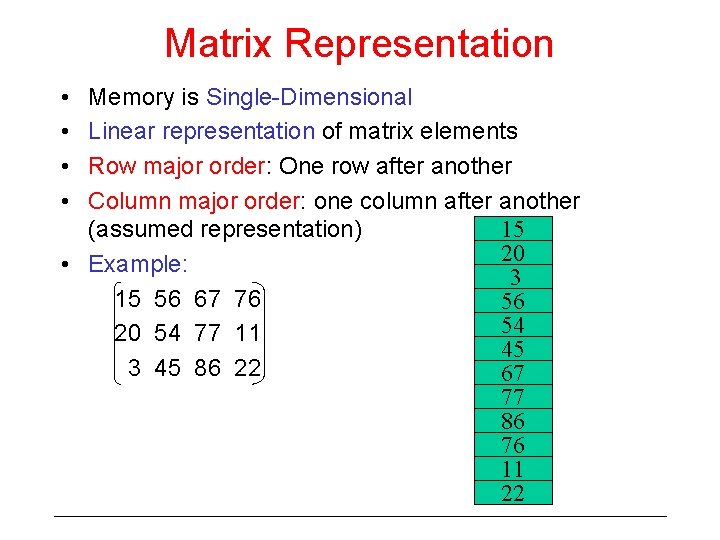
Matrix Representation • • Memory is Single-Dimensional Linear representation of matrix elements Row major order: One row after another Column major order: one column after another 15 (assumed representation) 20 • Example: 3 15 56 67 76 56 54 20 54 77 11 45 3 45 86 22 67 77 86 76 11 22

Initialization/Assignment • Using array constructor (column major order) A = ( 2, 3, 4, 5, 6 ) • Explicit nested do loops do I = 1, 5 do J = 1, 8 A(I, J) = I + J end do • Whole row/column assignment do I =1, 5 A(I, : ) = I end do • Initialization can be done at the time of declaration

Assignment • Whole, part or individual array elements can be assigned A =. . . A(: , i) =. . . A(i, j) = … • The rhs should be appropriate type • Lifting of scalar to suitable types may be required • with READ statements read *, ((A(i, j), j = 1, 3), I = 1, 4)

Using matrix variables • Matrix variables can be accessed, individually, in sections or as a whole • Used in expressions on the right hand side of any assignment • Intrinsic functions on base types lifted to matrix types • Eg. Abs, Sin, Cos, Tan, Log, Sqrt can be applied to a matrix variable – Sin(A) is a similar matrix in which each entry is Sin of the corresponding entries in A

Other intrinsic functions • • • LBOUND(A, d) – lower bound of index in the dimension d LBOUND(A) - list of lower bounds UBOUND - upper bound, similar SIZE(A, d) - number of entries in dimension d size(A) - total no. of elements SHAPE(A) - returns the `shape' of A – Extent in a dimension is the no. of entries in that dimension – Shape is an one dimensional array of extents(one entry per dimension)

Transformational Intrinsic Functions • Dot_Product(A, B) - dot product of one dimensional arrays of A and B • MATMUL(A, B) - Matrix multiplication on conformable matrices A and B • RESHAPE(A, B) - B is a one-dimensional shape array – Entries in A are converted into an array of shape B – Column major order used • Example: Suppose A = – Reshape(A, B) = 2 5 6 7 and B = [6, 2] 1328 7589 2 73 688 155279 • Usually used for initializing a matrix from a linear list of elements

Masked Assignment • A more generalized selection is possible using WHERE construct • Suppose, you want to multiply all entries > 0 by 2, and all other entries set to 0 then where (A > 0) A=2*A elsewhere A=0 end where • Note: Reference to an array has many connotations – context dependent

Accessing Matrix variables • When a matrix is accessed, the index values should be valid • illegal values lead to run-time error - Array index exceeding bounds • Compiler optionally inserts code for the check

Generalized Arrays • Multi-dimensional arrays are possible • All array operations, like declaration, initialization and use are similar • Rank of an array is the number of dimensions • One-dimensional array is of rank 1, matrix of rank 2 etc. • Arrays of up to rank 7 are allowed in Fortran

Memory Allocation • Arrays are allocated memory by the compiler • The allocation is static - done at compile time • More and larger arrays, larger the memory requirement • Array use and their size requirements should be done with care – indiscriminate use would result in wastage of memory • Use arrays only when all the data in the arrays are required at the same time in memory

Allocatable Arrays • Allocatable arrays is a solution to memory wastage problem • When the size of an input data set is unknown, better to use the following: real, dimension(), allocatable : : A integer, dimension(: ), allocatable : : B • This is a declaration of an Array A and B of rank 1 and 2 respectively • Only ranks specified, the extent decided dynamically • When A ( and B) initialized, the extents are decided and allocated • This enables avoiding static allocation of conservative estimate of required space

Allocate Construct • Allocatable arrays are allocated memory using explicit instruction: allocate(A(n), i) • This indicates the extent of A is the value of n • This is an external routine that may succeed or fail • Succeeds when the memory allocation is successful • The external procedure sends a value 0 via the parameter i • Typically the size is input by the user which is used in the allocation • Allocated memory can be deallocated using deallocate(A, i) • This succeeds provided the value returned via i is 0

Illustration Linear Systems of Equations • Most commonly occurring problem, the original motivation for matrices • solve a system of n equations in n variables a 11 x 1 + a 12 x 2 +. . . + a 1 nxn = b 1 a 12 x 2 + a 22 x 2 +. . . + a 2 nxn = b 2. . . an 1 x 1 + an 2 x 2 + … + annxn = bn • aij, , bj are all real numbers

Gaussian Elimination • choose any equation and any variable with non zero coefficient ( called pivot) in the equation • eliminate this variable from all other equations by adding a multiple of chosen equation • repeat with remaining equations • solve one equation in one variable • back substitute value of variable to find others • two steps, elimination and back substitution

Program real, dimension(: , : ), allocatable : : a integer : : n, i, j real, dimension(: ), allocatable : : x read *, n ! Number of variables allocate(x(n), stat=i) if ( i /= 0) then print *, "allocation of x failed" stop endif allocate(a(n, n+1), stat=i) if ( i /= 0) then print *, "allocation of array a failed" stop endif do i = 1, n print *, "enter coefficients of equation", i read *, a(i, 1: n+1) end do

do i = 1, n a(i, i: n+1) = a(i, i: n+1)/a(i, i) ! make coefficient of x_i 1. 0 do j = i+1, n a(j, i: n+1) = a(j, i: n+1) - a(i, i: n+1)*a(j, i) end do ! eliminate x_i end do do i = n, 1, -1 x(i) = a(i, n+1) - sum(a(i, i+1: n)*x(i+1: n)) end do ! sum of a null array is 0. 0 print *, "solution is" print *, x(1: n) deallocate(a, x, stat=i) if ( i /= 0) then print *, "deallocation failed" stop endif

Elimination • a(1: n+1, 1: n+1) contains the coefficients, x(1: n) the computed values of variables • assumes a(i, i) /= 0. 0 at every step • true for many special types of matrices • problem if abs(a(i, i)) is too small • elimination needs to be done only once for different right hand sides • only back substitution needs to be done • reduces operations from n 3 to n 2

Pivoting • swap rows and columns to make a(i, i) large • partial pivoting - swap row i with row containing maxval(abs(a(i: n, i))) – what if it is 0. 0? • complete pivoting- swap row and column to make a(i, i) = maxval(abs(a(i: n, i: n))) – what if it is still 0. 0? – this changes order of the variables • gives more accurate results but more time