Motion under constant acceleration Mr Weissbard Physics Standards

Motion under constant acceleration Mr. Weissbard

Physics Standards • CA content standards: Physics 1 c • Students know how to apply the law F=ma to solve one-dimensional motion problems that involve constant forces (Newton's second law). • NGSS: HS-PS 2 -1. • Analyze data to support the claim that Newton's second law of motion describes the mathematical relationship among the net force on a macroscopic object, its mass, and its acceleration. [Clarification Statement: Examples of data could include tables or graphs of position or velocity as a function of time for objects subject to a net unbalanced force, such as a falling object, an object rolling down a ramp, or a moving object being pulled by a constant force. ] [Assessment Boundary: Assessment is limited to one-dimensional motion and to macroscopic objects moving at non-relativistic speeds. ]

Learning Objective • To understand the behavior of objects under constant acceleration and to predict velocity and position using graphs and formulas. • Warm Up: {FM} Write the equation of motion (formula) for an object (particle) moving at constant velocity. Sketch.

Web Resources • video: Apollo 11 Launch: <a target="_blank" href= "https: //www. youtube. com/watch? v=F 0 Yd. Gx. J_QM">https: //www. youtube. com/watch? v=F 0 Yd -Gx. J_QM</a> • Questions: What did you observe? Why did the rocket's velocity increase? Why did they jettison the first stage rocket booster?

Average velocity Instantaneous velocity • What is velocity? • What does the word average mean? • What does the word instantaneous mean?

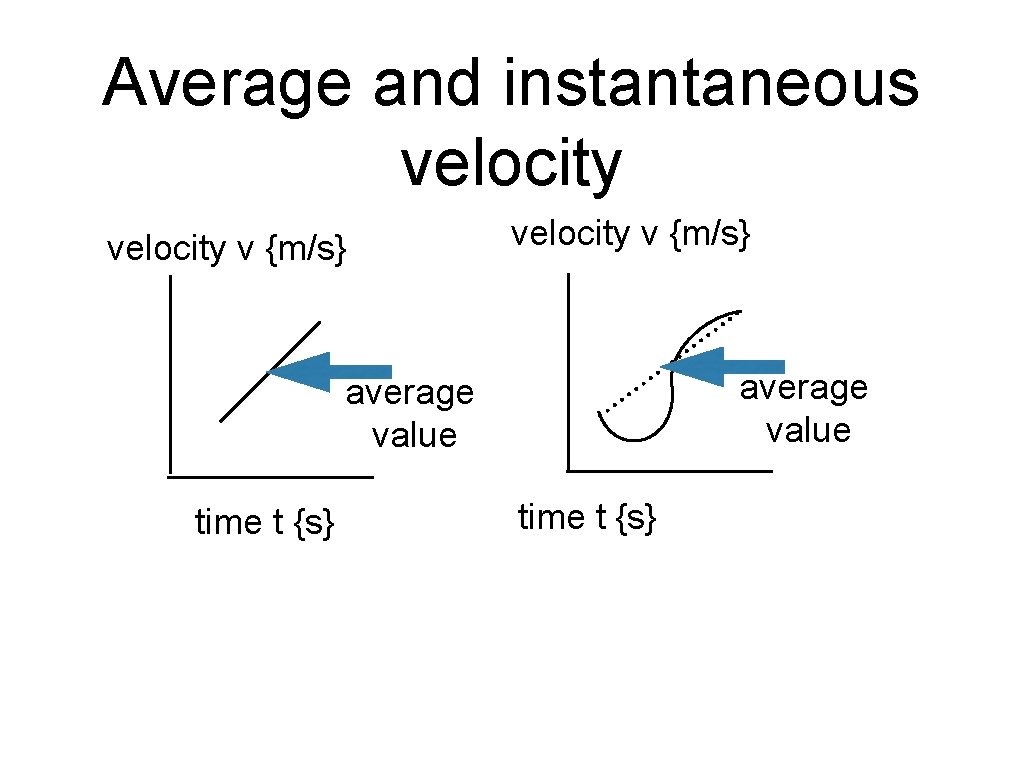
Average and instantaneous velocity v {m/s} average value time t {s}

How can we use velocity to calculate the distance an object travels? • • Suggest 2 ways to solve this problem • assume velocity is changing in a linear fashion i. e. straight line • hint: the distance travelled is the area under the curve d = vavg x t Does this formula apply to both graphs on the previous slide?

Find the distance travelled • Find 2 different ways to solve this problem v {m/s} 2 1 0 0 1 2 t {s}

Acceleration • Acceleration is defined as the change in velocity for a given time • Average acceleration is defined as the total change in velocity over a given period of time • Instantaneous acceleration is how the velocity is changing at a particular moment

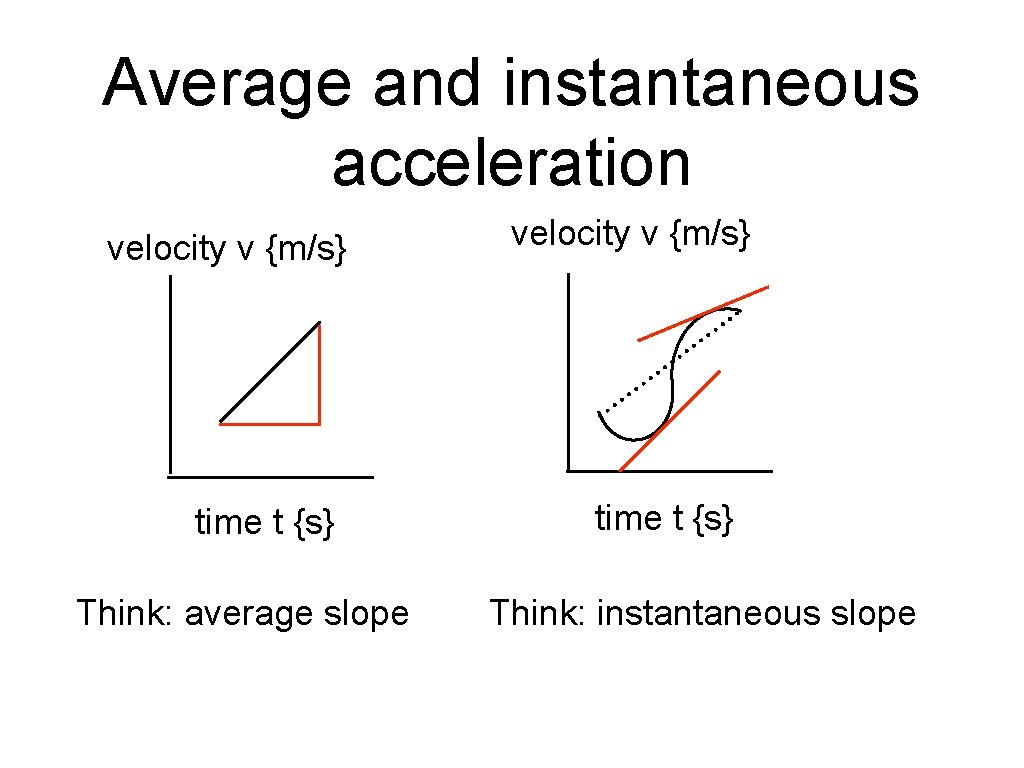
Average and instantaneous acceleration velocity v {m/s} time t {s} Think: average slope velocity v {m/s} time t {s} Think: instantaneous slope

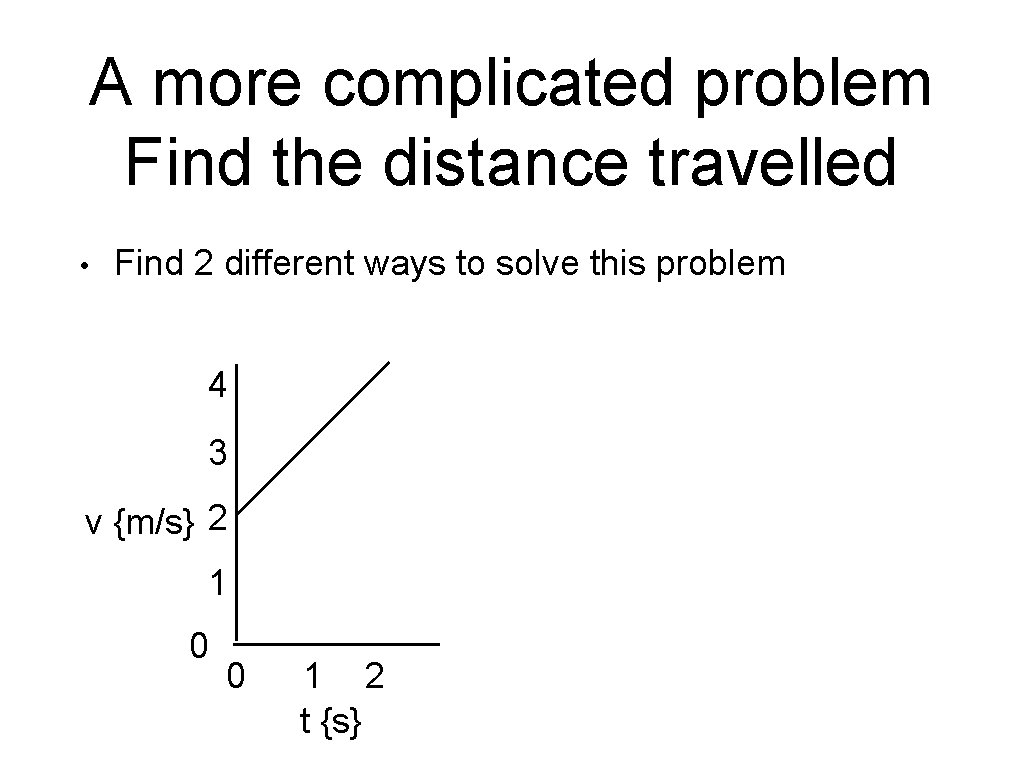
A more complicated problem Find the distance travelled • Find 2 different ways to solve this problem 4 3 v {m/s} 2 1 0 0 1 2 t {s}

Sample problems: • A bicycle is moving at 2 m/s when it crosses the starting line. The rider accelerates steadily at a rate of 1 m/s every second for 5 seconds. • How fast is he moving after 5 seconds? • What was his average velocity form 0 to 5 seconds? • How far did he travel in the 5 seconds after he crossed the staring line?

Wrap Up • What have we learned today? • the difference between average and instantaneous • how to find distance travelled from a v vs t graph • the definition of acceleration • formulas to calculate distance travelled (assuming constant acceleration)