Motion with Constant Acceleration Constant Acceleration In many



































- Slides: 39

Motion with Constant Acceleration

Constant Acceleration • In many practical situations: – The magnitude of the acceleration is uniform (constant) – The motion is in a straight line • It’s useful to derive some equations which apply in this special case ONLY!!! – The kinematic equations for constant (uniform) acceleration in one dimension.

Constant Acceleration • Derivation is in the text. Also partially on the next slide! Read on your own! • In the derivation, its useful to change notation slightly. • Note: My preferred notation is slightly different than our text!! t 1 0 = time when the problem begins x 1 x 0 = initial position (at t 1 = 0, often x 0 = 0) v 1 v 0 = initial velocity (at t 1 = 0) t 2 t = time when we wish to know other quantities x 2 x = position at time t v 2 v = velocity at time t a acceleration = constant (average & instantaneous accelerations are equal)

• By definition we have: – Average velocity: v = (x - x 0)/t (1) – Acceleration (average = instantaneous): a = (v - v 0)/t (2) – Average velocity (another form): v = (½)(v + v 0) (3)

Constant Acceleration Equations • Note Again: My preferred notation is slightly different than in our text!! • Results (one-dimensional motion only!): v = v 0 + at (1) x = x 0 + v 0 t + (½)a t 2 (2) v 2 = (v 0)2 + 2 a (x - x 0) (3) v = (½) (v + v 0) (4) NOT VALID UNLESS a = CONSTANT!!! Often, x 0 = 0. Sometimes v 0 = 0

Kinematic Equations – summary (In the notation of your text) Section 2. 6

Physics & Equations IMPORTANT!!! – Even though these equations & their applications are important, Physics is not a collection of formulas to memorize & blindly apply! – Physics is a set of PHYSICAL PRINCIPLES. – Blindly searching for the “equation which will work for this problem” is DANGEROUS!!!! – On exams, you get to have an 8. 5´´ 11´´ piece of paper, with anything written on it (both sides) you wish. On quizzes, I will give you relevant formulas.

All we need for 1 -dimensional constant-acceleration problems: NOT VALID UNLESS a = CONSTANT!!!

Kinematic Equations – Again (In the notation of your text) Section 2. 6

Problem Solving Strategies 1. Read the whole problem. Make sure you understand it. Read it again. 2. Decide on the objects under study & what the time interval is. 3. Draw a diagram & choose coordinate axes. 4. Write down the known (given) quantities, & the unknown ones needed. 5. What physics applies? Plan an approach to a solution. 6. Which equations relate known & unknown quantities? Are they valid in this situation? Solve algebraically for the unknown quantities, & check that your result is sensible (correct dimensions). 7. Calculate the solution, round it to appropriate number of significant figures. 8. Look at the result - is it reasonable? Does it agree with a rough estimate? 9. Check the units again.

Bottom Line: THINK! DO NOT BLINDLY APPLY FORMULAS!!!!

Example: Runway Design You’re designing an airport. A plane that will use this airport must reach a speed of vmin = 100 km/h (27. 8 m/s). It can accelerate at a = 2 m/s 2. (a) If the runway is x = 150 m long, can this plane reach the speed of before it runs off the end of the runway? (b) If not, what is the minimum length required for the runway? Table of Knowns & Unknowns (1) (2) (3) (4)

Example: Runway Design You’re designing an airport. A plane that will use this airport must reach a speed of vmin = 100 km/h (27. 8 m/s). It can accelerate at a = 2 m/s 2. (a) If the runway is x = 150 m long, can this plane reach the speed of before it runs off the end of the runway? (b) If not, what is the minimum length required for the runway? Solutions (a) Use Eq. (3): v 2 = (v 0)2 + 2 a(x – x 0) Table of Knowns & Unknowns v 2 = 0 + 2(2. 0)(150 – 0) = 600 m/s 2 So v = (600)½ = 24. 5 m/s Note that this means take the square root! That obviously matters! (1) (2) (3) (4)

Example: Runway Design You’re designing an airport. A plane that will use this airport must reach a speed of vmin = 100 km/h (27. 8 m/s). It can accelerate at a = 2 m/s 2. (a) If the runway is x = 150 m long, can this plane reach the speed of before it runs off the end of the runway? (b) If not, what is the minimum length required for the runway? Solutions (a) Use Eq. (3): v 2 = (v 0)2 + 2 a(x – x 0) v 2 = 0 + 2(2. 0)(150 – 0) = 600 m/s 2 So v = (600)½ = 24. 5 m/s Note that this means take the square root! That obviously matters! (b) Use Eq. (3) again with v = vmin = 27. 8 m/s. Solve for Table of Knowns & Unknowns (1) x – x 0 = [v 2 – (v 0)2]/(2 a) x = [(27. 8)2 – 0]/[2(2. 0)] So x = 193 m. To be safe, make the runway 200 m long! (2) (3) (4)

Example: Acceleration of a Car How long does it take a car to cross a 30 m wide intersection after the light turns green if it accelerates at a constant 2. 0 m/s 2? Obviously, it starts from rest!! Known: x 0 = 0, x = 30 m, v 0 = 0, a = 2. 0 m/s 2 Wanted: t.

Example: Acceleration of a Car How long does it take a car to cross a 30 m wide intersection after the light turns green if it accelerates at a constant 2. 0 m/s 2? Obviously, it starts from rest!! Known: x 0 = 0, x = 30 m, v 0 = 0, a = 2. 0 m/s 2 Wanted: t. Use: x = x 0 + v 0 t + (½)at 2 = 0 + (½)at 2 t = (2 x/a)½ = 5. 48 s NOTE! The square root obviously matters!

Example: Air Bags You need to design an air bag system that can protect the driver at a speed of 100 km/h = 28 m/s (60 mph) if the car hits a brick wall. Estimate how fast the air bag must inflate to effectively protect the driver. How does the use of a seat belt help the driver? Known: x 0 = v 0 = 28 m/s v=0 The car obviously stops when the crash ends! Wanted unknown: t. But we don’t know acceleration a or distance x either! Estimate x = 1. 0 m. This has to be a 2 step problem! (1) (2) (3) (4)

Example: Air Bags You need to design an air bag system that can protect the driver at a speed of 100 km/h = 28 m/s (60 mph) if the car hits a brick wall. Estimate how fast the air bag must inflate to effectively protect the driver. How does the use of a seat belt help the driver? Known: x 0 = v 0 = 28 m/s v=0 Car obviously stops when crash ends! Wanted unknown: t. But we don’t know acceleration a or distance x either! Estimate x = 1. 0 m This has to be a 2 step problem! First, use (2) to solve for a: 0 = (v 0)2 + 2 a(x – 0) so a = - (v 0)2∕(2 x) = - (28)2 ∕(2) = - 390 m/s 2 (1) This is a HUGE acceleration!! (2) (3) (4)

Example: Air Bags You need to design an air bag system that can protect the driver at a speed of 100 km/h = 28 m/s (60 mph) if the car hits a brick wall. Estimate how fast the air bag must inflate to effectively protect the driver. How does the use of a seat belt help the driver? Known: x 0 = v 0 = 28 m/s v=0 Car obviously stops when crash ends! Wanted unknown: t. But we don’t know acceleration a or distance x either! Estimate x = 1. 0 m This has to be a 2 step problem! First, use (2) to solve for a: 0 = (v 0)2 + 2 a(x – 0) so a = - (v 0)2∕(2 x) = - (28)2 ∕(2) = - 390 m/s 2 (1) This is a HUGE acceleration!! Now, use (1) to solve for t: 0 = v 0 + at so (2) (3) t = - (v 0) ∕a = 0. 07 s !!! (4)

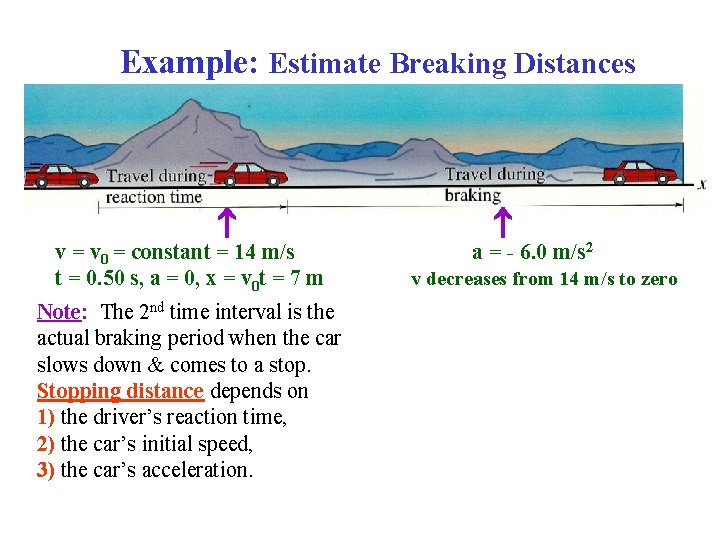
Example: Estimate Breaking Distances v = v 0 = constant = 14 m/s t = 0. 50 s, a = 0 Note: The 2 nd time interval is the actual braking period when the car slows down & comes to a stop. Stopping distance depends on 1) the driver’s reaction time, 2) the car’s initial speed, 3) the car’s acceleration. a = - 6. 0 m/s 2 v decreases from 14 m/s to zero

Example: Estimate Breaking Distances v = v 0 = constant = 14 m/s t = 0. 50 s, a = 0, x = v 0 t = 7 m Note: The 2 nd time interval is the actual braking period when the car slows down & comes to a stop. Stopping distance depends on 1) the driver’s reaction time, 2) the car’s initial speed, 3) the car’s acceleration. a = - 6. 0 m/s 2 v decreases from 14 m/s to zero

Example: Estimate Breaking Distances v = v 0 = constant = 14 m/s t = 0. 50 s, a = 0, x = v 0 t = 7 m Note: The 2 nd time interval is the actual braking period when the car slows down & comes to a stop. Stopping distance depends on 1) the driver’s reaction time, 2) the car’s initial speed, 3) the car’s acceleration. a = - 6. 0 m/s 2, x 0 = 7 m v decreases from 14 m/s to zero v 0 = 14 m/s, v = 0 v 2 = (v 0)2 + 2 a(x – x 0) x = x 0 + [v 2 - (v 0)2]/(2 a) x = 7 m + 16 m = 23 m

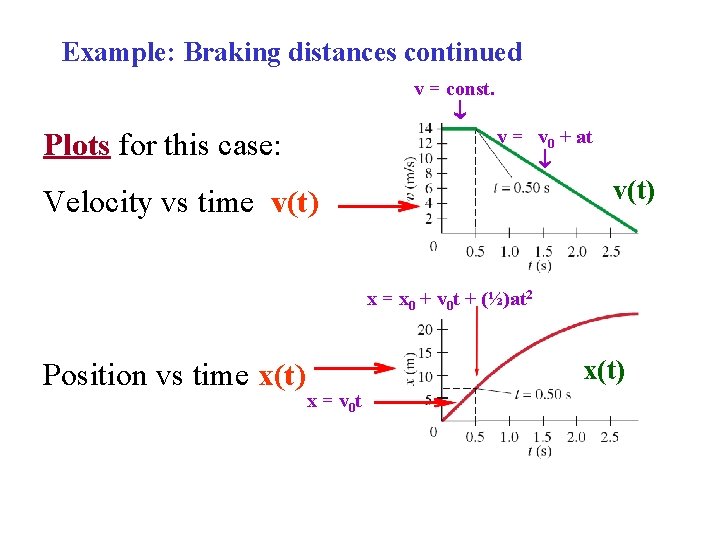
Example: Braking distances continued v = const. v = v 0 + at Plots for this case: v(t) Velocity vs time v(t) x = x 0 + v 0 t + (½)at 2 Position vs time x(t) x = v 0 t

Example: Fastball Known: x 0 = 0, x = 3. 5 m, v 0 = 0, v = 44 m/s Wanted: a

Example: Fastball Known: x 0 = 0, x = 3. 5 m, v 0 = 0, v = 44 m/s Wanted: a Use: v 2 = (v 0)2 + 2 a (x - x 0) a = (½)[v 2 - (v 0)2]/(x - x 0) = 280 m/s 2 !

Example: 2 Moving Objects: Police & Speeder A car, speeding at v 0 S = 150 km/h (42 m/s) passes a still police car (v 0 P = 0) which immediately takes off (accelerates!) in hot pursuit. Using simple assumptions, such as that the speeder continues at constant speed v 0 S = 42 m/s (& also for the acceleration a. P of the police car!), ESTIMATE how long it takes the police car to overtake the speeder. Then ESTIMATE the police car’s speed at that moment & decide if the assumptions were reasonable.

Example: 2 Moving Objects: Police & Speeder A car, speeding at v 0 S = 150 km/h (42 m/s) passes a still police car (v 0 P = 0) which immediately takes off (accelerates!) in hot pursuit. Using simple assumptions, such as that the speeder continues at constant speed v 0 S = 42 m/s (& also for the acceleration a. P of the police car!), ESTIMATE how long it takes the police car to overtake the speeder. Then ESTIMATE the police car’s speed at that moment & decide if the assumptions were reasonable. Note! Before working this problem, we need to work another problem, which will give us an ESTIMATE of the acceleration a. P of the police car. In order to do this, we take numbers from ads for the type of car the police drive. These claim that this car can accelerate from rest to 100 km/h (28 m/s) in 5. 0 s. Using v = v 0 + a. Pt with these numbers gives 28 = 0 + a. P(5) or a. P = 5. 6 m/s 2. So, to solve this problem of the police car catching up to the speeder, we use this ESTIMATE for the acceleration a. P

Problem now restated is: A car, speeding at v 0 S = 150 km/h (42 m/s) passes a still police car (v 0 P = 0) which immediately takes off (accelerates!) in hot pursuit. Assume that the speeder continues at constant speed v 0 S = 42 m/s & that a. P = 5. 6 m/s 2. ESTIMATE how long it takes the police car to overtake the speeder. Then ESTIMATE the police car’s speed at that time & decide if the assumptions were reasonable.

Problem now restated is: A car, speeding at v 0 S = 150 km/h (42 m/s) passes a still police car (v 0 P = 0) which immediately takes off (accelerates!) in hot pursuit. Assume that the speeder continues at constant speed v 0 S = 42 m/s & that a. P = 5. 6 m/s 2. ESTIMATE how long it takes the police car to overtake the speeder. Then ESTIMATE the police car’s speed at that time & decide if the assumptions were reasonable. Solution: The speeder moves at constant speed v 0 S = 42 m/s so, at some time t later it has moved a distance x. S = v 0 St In that same time t the police car has moved a distance x. P = (½)a. Pt 2 When the police car catches the speeder, the two distances must be the same. So, we equate them and solve for t: x. S = v 0 St = x. P = (½)a. Pt 2. This is a quadratic equation for t, which has solutions; t = 0 & t = 15 s.

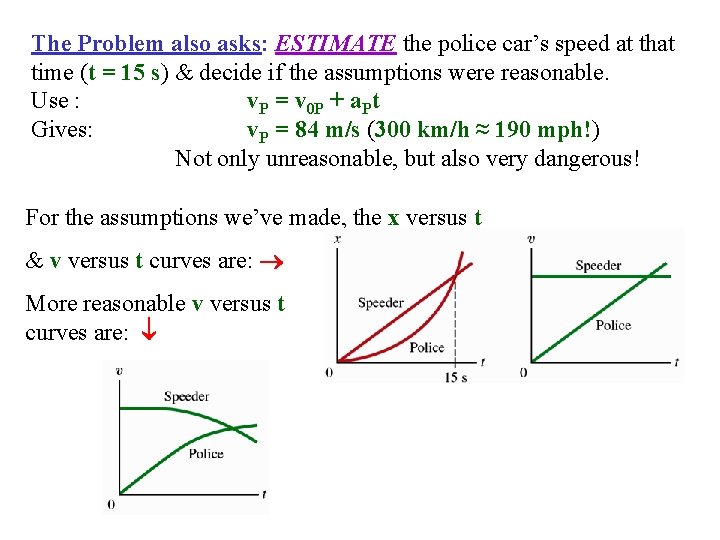
The Problem also asks: ESTIMATE the police car’s speed at that time (t = 15 s) & decide if the assumptions were reasonable. Use : v. P = v 0 P + a. Pt

The Problem also asks: ESTIMATE the police car’s speed at that time (t = 15 s) & decide if the assumptions were reasonable. Use : v. P = v 0 P + a. Pt Gives: v. P = 84 m/s (300 km/h ≈ 190 mph!) Not only unreasonable, but also very dangerous! For the assumptions we’ve made, the x versus t & v versus t curves are: More reasonable v versus t curves are:

Example: Carrier Landing A jet lands on an aircraft carrier at velocity v 0 = 140 km/h (63 m/s). a) Calculate the acceleration (assumed constant) if it stops in t = 2. 0 s due to the arresting cable that snags the airplane & stops it. b) If it touches down at position x 0 = 0, calculate it’s final position.

Example: Carrier Landing A jet lands on an aircraft carrier at velocity v 0 = 140 km/h (63 m/s). a) Calculate the acceleration (assumed constant) if it stops in t = 2. 0 s due to the arresting cable that snags the airplane & stops it. b) If it touches down at position x 0 = 0, calculate it’s final position. Solutions a) v 0 = 63 m/s, t = 2. 0 s = time to stop. When it is stopped, v = 0. So, use v = v 0 + at = 0, which gives a = - (v 0/t) = - (63/2) = -31. 5 m/s 2

Example: Carrier Landing A jet lands on an aircraft carrier at velocity v 0 = 140 km/h (63 m/s). a) Calculate the acceleration (assumed constant) if it stops in t = 2. 0 s due to the arresting cable that snags the airplane & stops it. b) If it touches down at position x 0 = 0, calculate it’s final position. Solutions a) v 0 = 63 m/s, t = 2. 0 s = time to stop. When it is stopped, v = 0. So, use v = v 0 + at = 0, which gives a = - (v 0/t) = - (63/2) = -31. 5 m/s 2 b) Use x = x 0 + v 0 t + (½)at 2 , which gives x = x 0 + v 0 t + (½)at 2 = 0 + (63)(2) + (½)(-31. 5)(2)2 x = 63 m

Watch Out for the Speed Limit! Problem: A car traveling at a constant velocity of magnitude 41. 4 m/s passes a trooper hidden behind a billboard. One second after the speeding car passes the billboard, the trooper sets out from the billboard to catch it, accelerating at a constant rate of 3. 90 m/s 2. How long does it take her to overtake the speeding car?

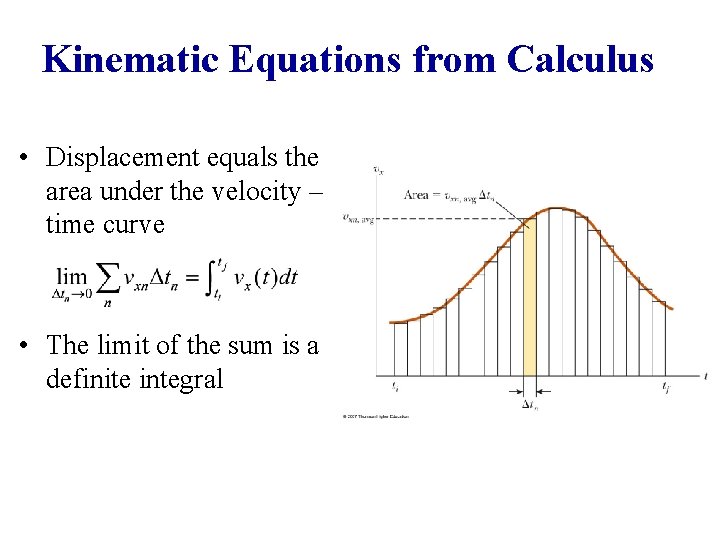
Kinematic Equations from Calculus • Displacement equals the area under the velocity – time curve • The limit of the sum is a definite integral

Kinematic Equations General Calculus Form

Kinematic Equations – Calculus Form with Constant Acceleration • The integration form of vf – vi gives • The integration form of xf – xi gives

Kinematic Equations – summary (In the notation of your text) Section 2. 6