Modelling and Solving English Peg Solitaire Chris Jefferson





![Model B: CSP • Problem constraints can be stated on moves[] alone. • Consider Model B: CSP • Problem constraints can be stated on moves[] alone. • Consider](https://slidetodoc.com/presentation_image_h/d6a207719c014a9d436b305ee6403812/image-8.jpg)













- Slides: 29

Modelling and Solving English Peg Solitaire Chris Jefferson, Angela Miguel, Ian Miguel, Armagan Tarim. AI Group Department of Computer Science University of York

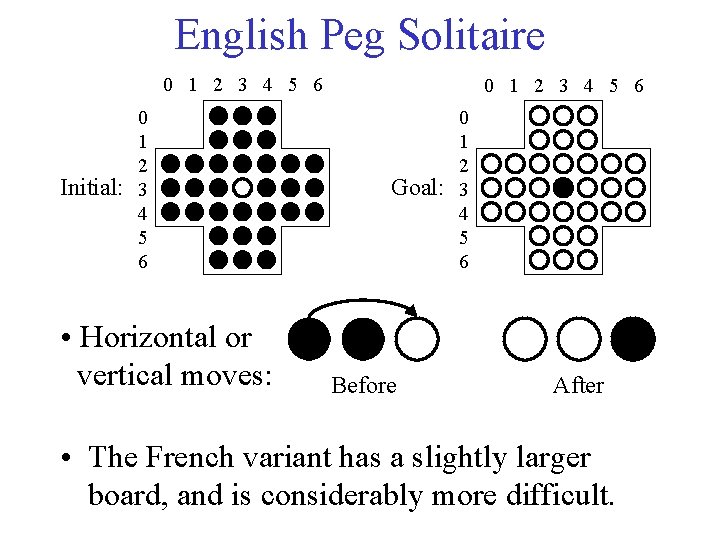
English Peg Solitaire 0 1 2 3 4 5 6 Initial: 0 1 2 3 4 5 6 • Horizontal or vertical moves: 0 1 2 3 4 5 6 Goal: Before 0 1 2 3 4 5 6 After • The French variant has a slightly larger board, and is considerably more difficult.

Solitaire: Interesting Features • A challenging search problem. • Highly symmetric. • Symmetries of the board, symmetries of moves. • Planning-style problem. • Not usually tackled directly with constraint satisfaction/integer programming.

Model A: IP • 31 moves required to solve a single-peg reversal. • Exploit this in the modelling. • b. State[i, j, t] {0, 1}. • describes the state of the board at time-step t = 0, …, 31. • M[i, j, t, d] {0, 1}. 1. denotes whether a move was made from location i, j at time-step t. d in {N, S, E, W}.

Model A: IP Move Conditions: `1’ means move made. Connecting board states. Consider all moves affecting a position

Model A: IP One move at a time: Objective function. Minimise:

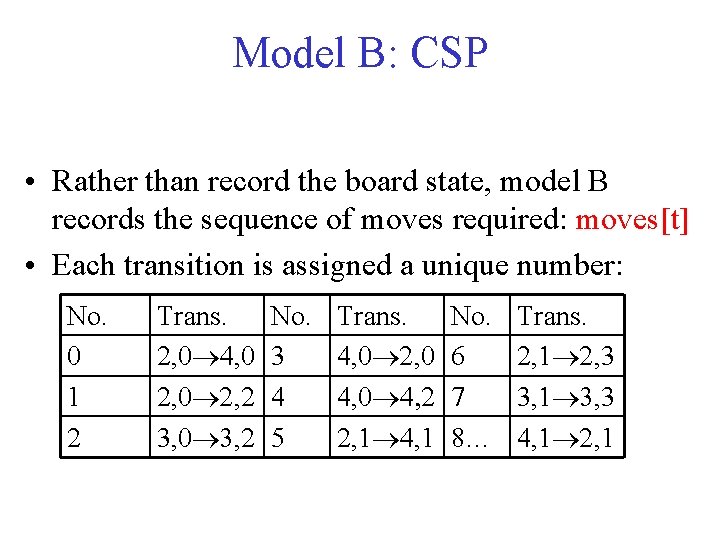
Model B: CSP • Rather than record the board state, model B records the sequence of moves required: moves[t] • Each transition is assigned a unique number: No. 0 1 2 Trans. 2, 0 4, 0 2, 2 3, 0 3, 2 No. 3 4 5 Trans. 4, 0 2, 0 4, 2 2, 1 4, 1 No. 6 7 8… Trans. 2, 1 2, 3 3, 1 3, 3 4, 1 2, 1
![Model B CSP Problem constraints can be stated on moves alone Consider Model B: CSP • Problem constraints can be stated on moves[] alone. • Consider](https://slidetodoc.com/presentation_image_h/d6a207719c014a9d436b305ee6403812/image-8.jpg)
Model B: CSP • Problem constraints can be stated on moves[] alone. • Consider transition 0: 2, 0 4, 0 at time-step t. The following must hold at time-step t-1. 0 1 2 3 4 5 6 • There must be pegs at 2, 0 and 3, 0. • There must be a hole at 4, 0. 0 1 • Ensure by imposing constraints on moves[1. . t-1]: Drawback: many such constraints needed. Some of very large size.

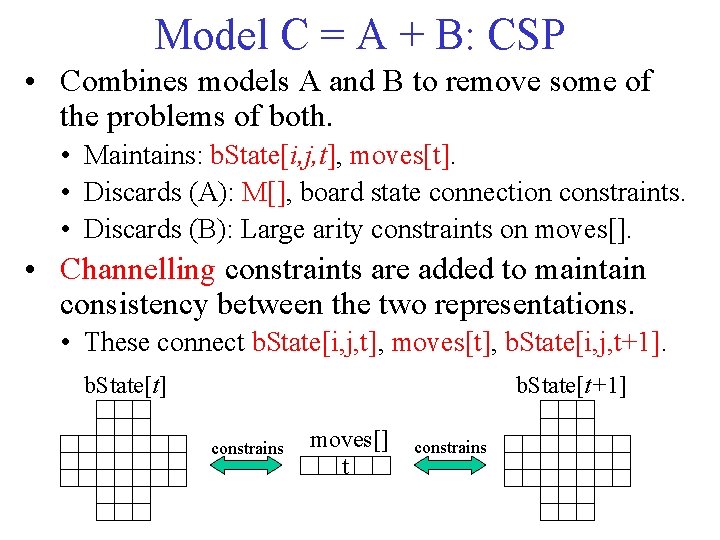
Model C = A + B: CSP • Combines models A and B to remove some of the problems of both. • Maintains: b. State[i, j, t], moves[t]. • Discards (A): M[], board state connection constraints. • Discards (B): Large arity constraints on moves[]. • Channelling constraints are added to maintain consistency between the two representations. • These connect b. State[i, j, t], moves[t], b. State[i, j, t+1]. b. State[t] b. State[t+1] constrains moves[] t constrains

Model C Channelling Constraints Changes(i, j): set of transitions that change the state of i, j peg. In(i, j): set of transitions that place a peg at i, j peg. Out(i, j): set of transitions that remove a peg from i, j • These constraints closely resemble pre- and postconditions of an AI Planning-style operator.

Results: Central Solitaire • Model A (IP): No solution in 12 hours. • Several alternative formulations also failed. • Reason: artificial objective function, hence no tight bounds to exploit. • Model B (CP): Exhausts memory. • Model C (A+B, CP solver): 16 seconds. • So: • Develop model C further. • Apply to other variations of Solitaire.

Pagoda Functions • Used to spot dead-ends early. • Value assigned to each board position such that: • Given positions a, b, c in a horizontal/vertical line: a+b c. • Pagoda value of a board state: • Sum of values at positions where there is a peg. • Monotonically decreasing as moves made: • Pagoda condition: a b c • If pagoda value for an intermediate position is less than that of final position, backtrack.

Pagoda Functions: Examples • For a single-peg Solitaire reversal at position i, j, want pagoda functions with non-zero entries at i, j. • Otherwise no pruning. • A rotation of one of these three gives a useful pagoda function for every board position: 1 1 1 1 1 1 1

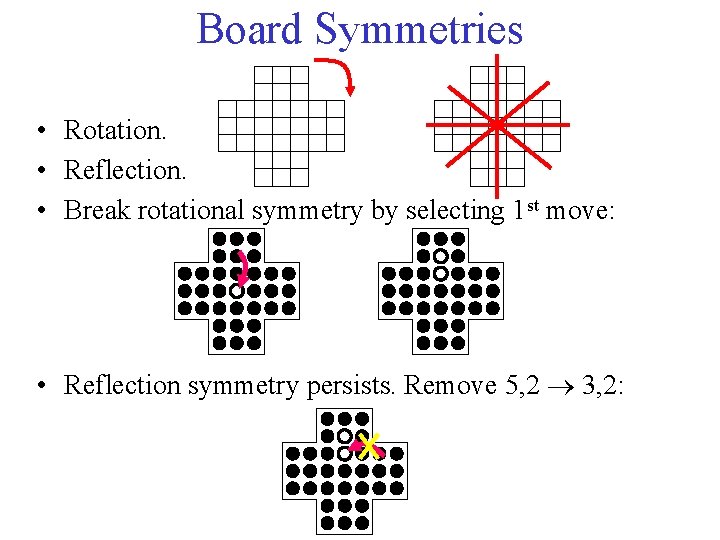
Board Symmetries • Rotation. • Reflection. • Break rotational symmetry by selecting 1 st move: • Reflection symmetry persists. Remove 5, 2 3, 2:

Board Symmetries • Further into the search are both broken and reestablished, depending on the moves made. • Breaking this symmetry is a possible application for SBDS or SBDD.

Symmetries of Independent Moves • Many pairs of moves can be performed in any order without affecting the rest of the solutions. • Two transitions are independent iff: • The set of pegs upon which they operate do not intersect. • Break this symmetry by ordering adjacent entries in moves[]: • independent(moves[i], moves[i+1]) moves[i] moves[i+1] • This problem extends to larger sets of transitions. • If 2 is independent of {3, 1}, can have 2, 3, 1 and 3, 1, 2.

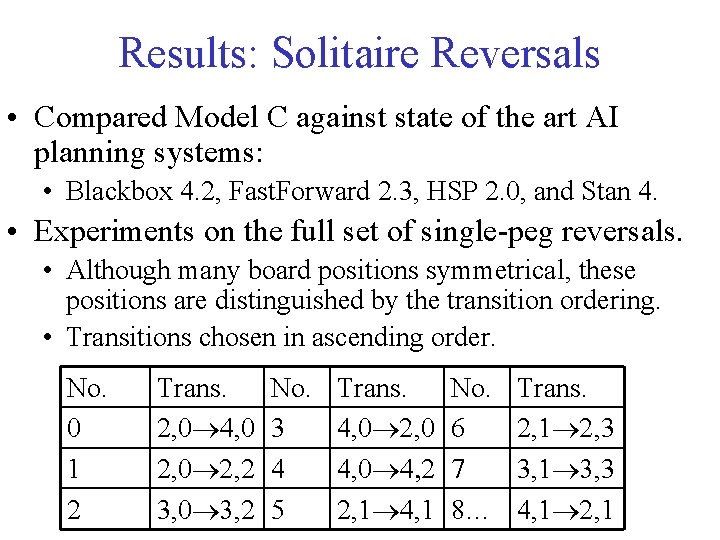
Results: Solitaire Reversals • Compared Model C against state of the art AI planning systems: • Blackbox 4. 2, Fast. Forward 2. 3, HSP 2. 0, and Stan 4. • Experiments on the full set of single-peg reversals. • Although many board positions symmetrical, these positions are distinguished by the transition ordering. • Transitions chosen in ascending order. No. 0 1 2 Trans. 2, 0 4, 0 2, 2 3, 0 3, 2 No. 3 4 5 Trans. 4, 0 2, 0 4, 2 2, 1 4, 1 No. 6 7 8… Trans. 2, 1 2, 3 3, 1 3, 3 4, 1 2, 1

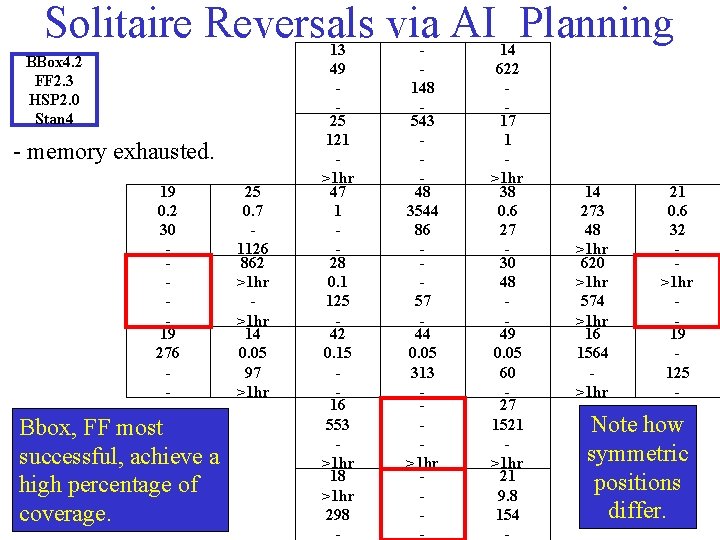
Solitaire Reversals via AI Planning BBox 4. 2 FF 2. 3 HSP 2. 0 Stan 4 - memory exhausted. 19 0. 2 30 19 276 - Bbox, FF most successful, achieve a high percentage of coverage. 25 0. 7 1126 862 >1 hr 14 0. 05 97 >1 hr 13 49 25 121 >1 hr 47 1 28 0. 1 125 42 0. 15 16 553 >1 hr 18 >1 hr 298 - 148 543 48 3544 86 57 44 0. 05 313 >1 hr - 14 622 17 1 >1 hr 38 0. 6 27 30 48 49 0. 05 60 27 1521 >1 hr 21 9. 8 154 - 14 273 48 >1 hr 620 >1 hr 574 >1 hr 16 1564 >1 hr 21 0. 6 32 >1 hr 19 125 - Note how symmetric positions differ.

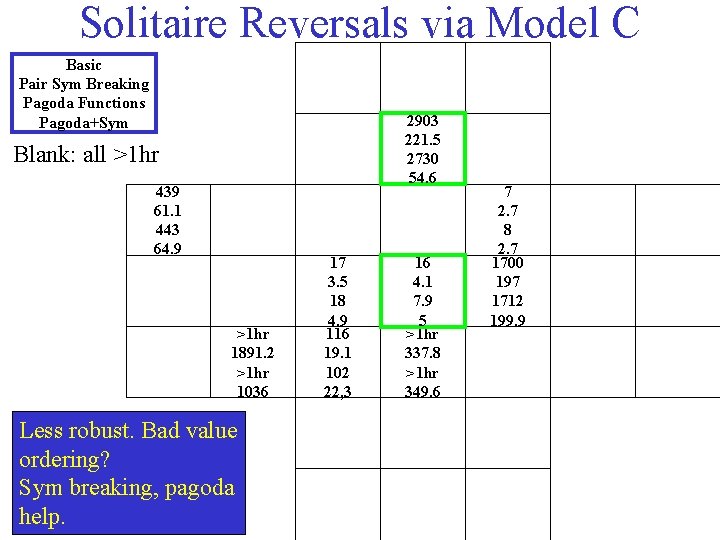
Solitaire Reversals via Model C Basic Pair Sym Breaking Pagoda Functions Pagoda+Sym 2903 221. 5 2730 54. 6 Blank: all >1 hr 439 61. 1 443 64. 9 >1 hr 1891. 2 >1 hr 1036 Less robust. Bad value ordering? Sym breaking, pagoda help. 17 3. 5 18 4. 9 116 19. 1 102 22, 3 16 4. 1 7. 9 5 >1 hr 337. 8 >1 hr 349. 6 7 2. 7 8 2. 7 1700 197 1712 199. 9

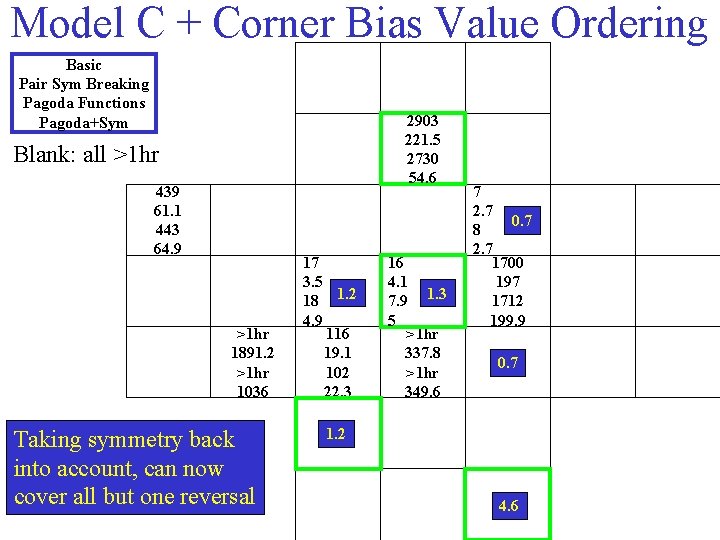
Model C + Corner Bias Value Ordering Basic Pair Sym Breaking Pagoda Functions Pagoda+Sym 2903 221. 5 2730 54. 6 Blank: all >1 hr 439 61. 1 443 64. 9 >1 hr 1891. 2 >1 hr 1036 Taking symmetry back into account, can now cover all but one reversal 17 3. 5 18 1. 2 4. 9 116 19. 1 102 22, 3 16 4. 1 7. 9 1. 3 5 >1 hr 337. 8 >1 hr 349. 6 7 2. 7 0. 7 8 2. 7 1700 197 1712 199. 9 0. 7 1. 2 4. 6

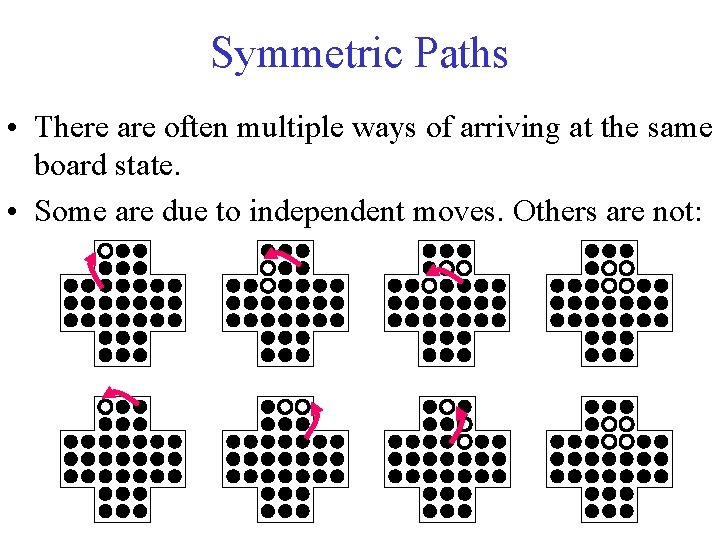
Symmetric Paths • There are often multiple ways of arriving at the same board state. • Some are due to independent moves. Others are not:

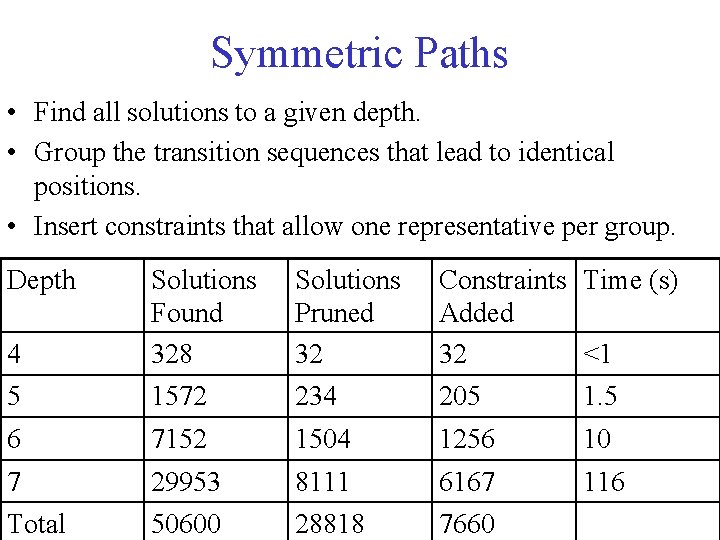
Symmetric Paths • Find all solutions to a given depth. • Group the transition sequences that lead to identical positions. • Insert constraints that allow one representative per group. Depth 4 Solutions Found 328 Solutions Pruned 32 Constraints Time (s) Added 32 <1 5 1572 234 205 1. 5 6 7152 1504 1256 10 7 29953 8111 6167 116 Total 50600 28818 7660

Fool’s Solitaire • An optimisation variant. • Reach a position where no further moves are possible in the shortest sequence of moves. • Not easily stated as an AI planning problem. • Shows the flexibility of the CP and IP approaches.

Fool’s Solitaire: IP Model • Moves, connection of board states same as model A. C[i, j, t]=1 iff there is a peg at position i, j with a legal move. New objective function. Minimise:

Fool’s Solitaire: CP Model • Modified version of model C. • An extra transition, dead. End, is added to the domain of the moves[] variables. • Assigned when no other move is possible. • dead. End transition is only allowed when no other transitions are possible. • Preconditions based on b. State[]. • If dead. End at moves[t], then also at all following time-steps:

Fool’s Solitaire: Results • CP, reverse instantiation order: 20 s • IP, iterative approach: 27 s

Conclusions • Basic, and ineffective CP and IP models combined into a superior CP model. • Another instance of the utility of channelling between two complementary models. • Each allows easy statement of different aspects of the problem: • Model A: preconditions on state changes without considering entire move history. • Model B: one move at once, combines 3 state changes into a single token.

Conclusions • Encouraging results versus dedicated AI planning systems. • Lessons learned should generalise to other sequential planning-style problems. • Channelling constraints specify action pre- and post-conditions. • Breaking symmetry of independent actions/paths.

Future Work • Further configurations of English Solitaire. • Other optimisation variants: • Minimise number of draughts-like multiple moves using a single peg. • Proving unsolvability. • Large search space to explore. • Will need improved symmetry breaking. • French Solitaire.
 Peg solitaire solution triangle
Peg solitaire solution triangle Problem solving and modelling task
Problem solving and modelling task Apba football solitaire
Apba football solitaire Bitcoin solitaire ‑ get real f...
Bitcoin solitaire ‑ get real f... Windows xp easter eggs
Windows xp easter eggs Parenteral nutrition types
Parenteral nutrition types Worm and sector steering gear
Worm and sector steering gear Which geometric modeling has ambiguous representation
Which geometric modeling has ambiguous representation Trendlines and regression analysis
Trendlines and regression analysis John adams vs thomas jefferson venn diagram
John adams vs thomas jefferson venn diagram Jefferson memorial deteriorating
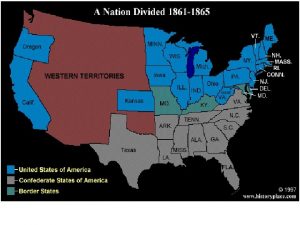
Jefferson memorial deteriorating Venn diagram abraham lincoln and jefferson davis
Venn diagram abraham lincoln and jefferson davis Jefferson davis strengths and weaknesses
Jefferson davis strengths and weaknesses Keburukan peg sebagai basis suppositoria adalah..
Keburukan peg sebagai basis suppositoria adalah.. Peg letkun asennus
Peg letkun asennus Peg pej
Peg pej The transition peg for a left turn is _?_.
The transition peg for a left turn is _?_. Sta je gastrostoma
Sta je gastrostoma Peg-pej
Peg-pej Objective of earthquake
Objective of earthquake Axle peg inventor train
Axle peg inventor train Peg capital fee
Peg capital fee Transition peg for left turn
Transition peg for left turn Taocoin
Taocoin Peg sonde mickey button
Peg sonde mickey button Peg sud
Peg sud Sonda peg
Sonda peg Peg word psychology
Peg word psychology Peg ville de lille
Peg ville de lille Peg disfagia
Peg disfagia