Mnohostny Prof RNDr Josef Molnr CSc PF UP

Mnohostěny Prof. RNDr. Josef Molnár, CSc. , PřF UP v Olomouci Univerzita třetího věku

Rozcvička: Krychle má 9 různých rovin symetrie. Nakreslete je.

Mnohostěn n je část prostoru ohraničeného konečným počtem rovinných mnohoúhelníků.

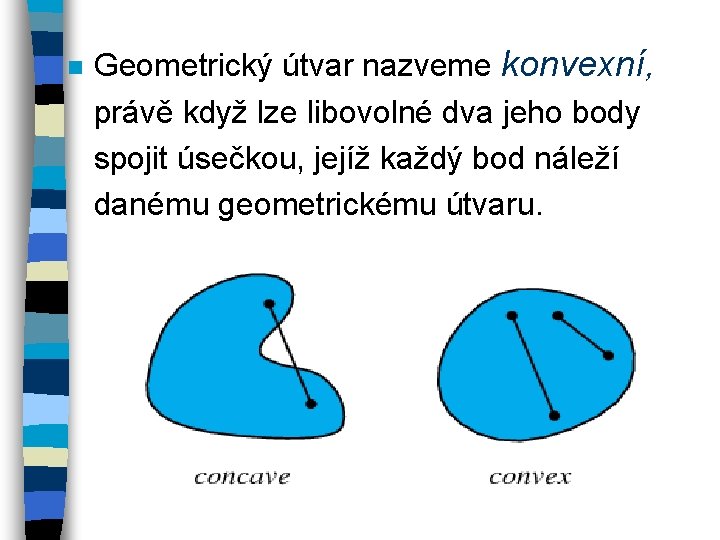
n Geometrický útvar nazveme konvexní, právě když lze libovolné dva jeho body spojit úsečkou, jejíž každý bod náleží danému geometrickému útvaru.

Eulerova charakteristika mnohostěnu Leonhard Euler 1707 - 1783 je číslo E=s+v–h kde s je počet stěn, v počet vrcholů a h počet hran daného konvexního mnohostěnu.

Eulerova věta „ V každém konvexním mnohostěnu platí Eulerův vztah s+v–h=2 kde s je počet stěn, v počet vrcholů a h počet hran daného konvexního mnohostěnu. “

Keplerův „Kosmický pohár“ - sféra Merkuru - opsán osmistěn, který je - vepsán do sféry Venuše - sféře Venuše opsán dvacetistěn - sféra Země - dvanáctistěn - sféra Marsu - čtyřstěn - sféra Jupitera - krychle - sféra Saturnu Johannes Kepler 1571 - 1630

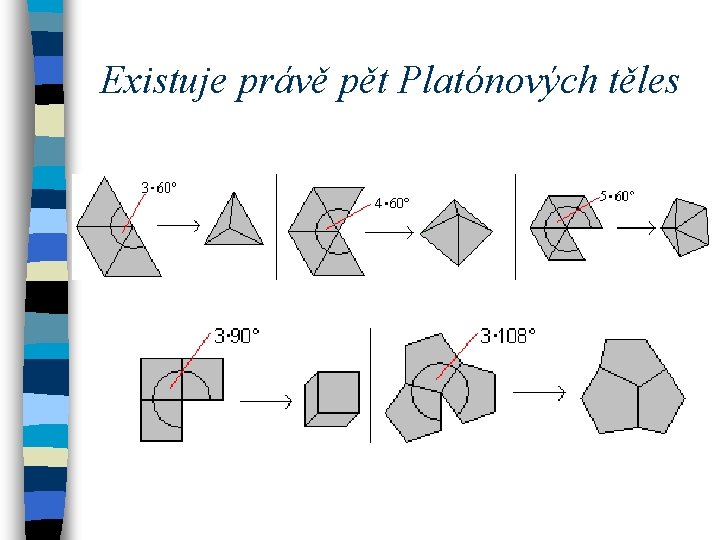
Existuje právě pět Platónových těles

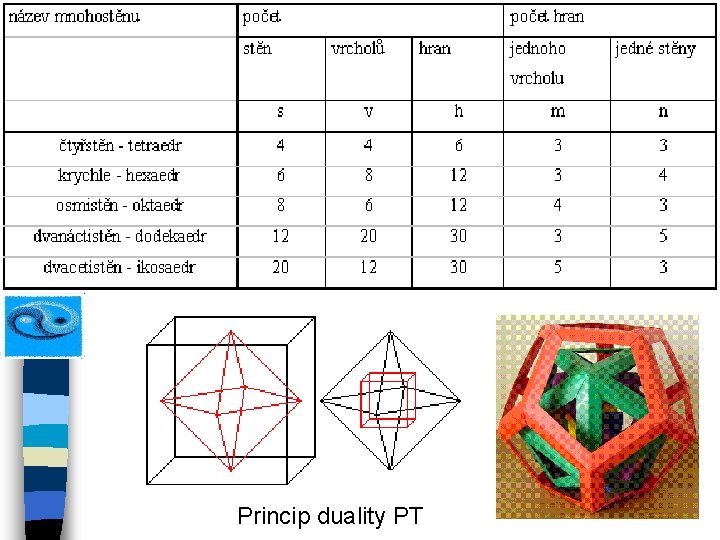
Princip duality PT

Deltatopy n n V definici PT vynecháme požadavek na stejnou valenci vrcholů (q) a „mnohoúhelníky“ nahradíme „trojúhelníky“. Existuje právě 8 deltatopů. Název deltatopu v h s q=3 q=4 q=5 1. čtyřstěn 4 6 4 4 0 0 2. dvojitý čtyřstěn 5 9 6 2 3 0 3. osmistěn 6 12 8 0 6 0 4. dvojitý pětiboký jehlan 7 15 10 0 5 2 5. siamský dvanáctistěn 8 18 12 0 4 4 6. 9 21 14 0 3 6 7. 10 24 16 0 2 8 12 30 20 0 0 12 8. dvacetistěn

Archimédova tělesa Archimédes ze Syrakus 287 – 212 př. n. l. - lze vytvořit z PT odříznutím vrcholů nebo hran tak, aby vznikly pravidelné konvexní mnohoúhelníky.

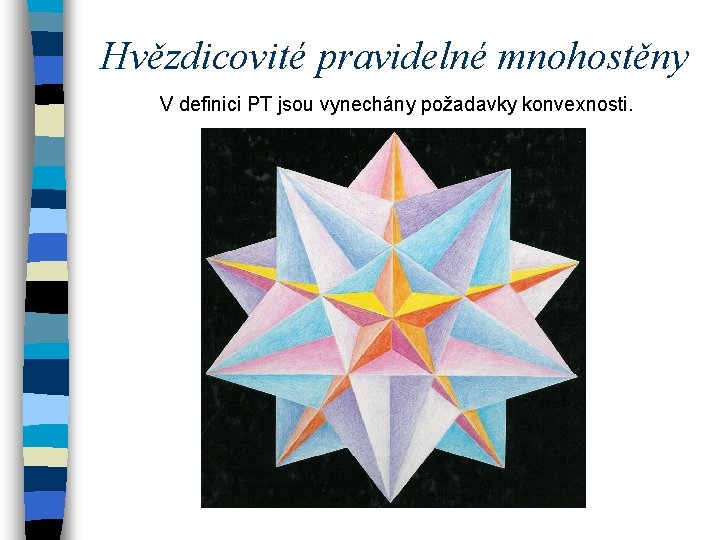
Hvězdicovité pravidelné mnohostěny V definici PT jsou vynechány požadavky konvexnosti.

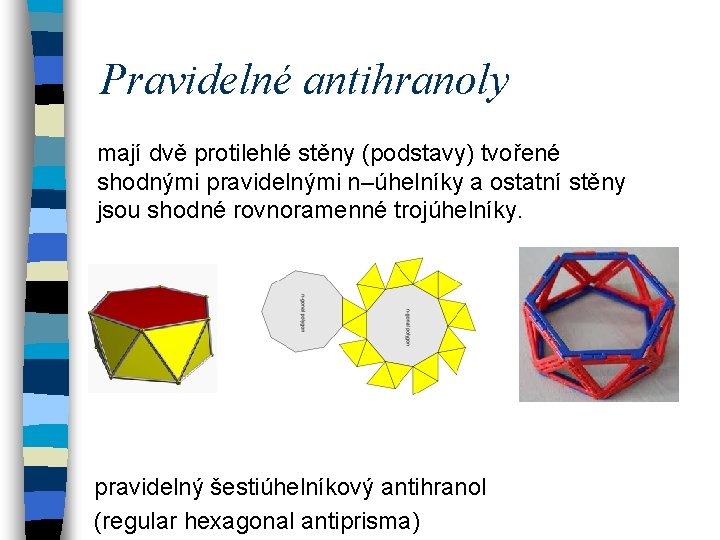
Pravidelné antihranoly mají dvě protilehlé stěny (podstavy) tvořené shodnými pravidelnými n–úhelníky a ostatní stěny jsou shodné rovnoramenné trojúhelníky. pravidelný šestiúhelníkový antihranol (regular hexagonal antiprisma)

Platónova tělesa v biosféře Mřížovka červená Virus dětské obrny Radiolaria (mřížovci)

Poincarého zobecnění Eulerovy věty n Pro mnohostěny platí s + v - h = 2 - 2 r, kde r je (topologický) rod plochy. Zjednodušeně lze říci, že hodnota rodu plochy je rovna počtu v ní existujících „průchodů“.

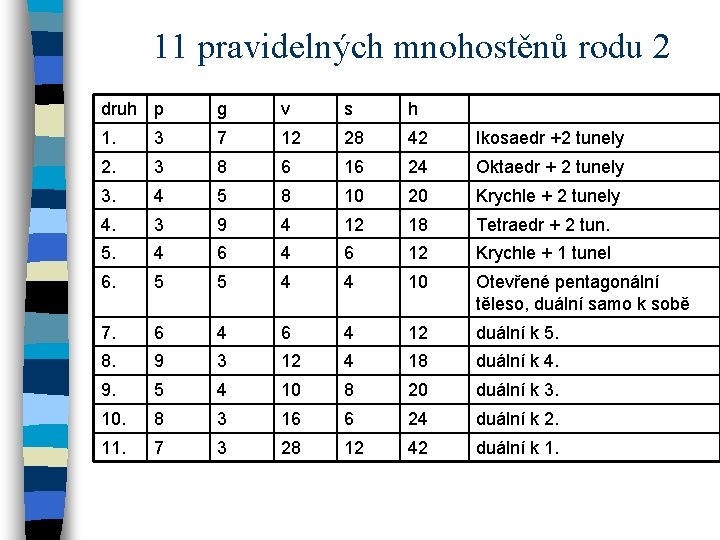
11 pravidelných mnohostěnů rodu 2 druh p g v s h 1. 3 7 12 28 42 Ikosaedr +2 tunely 2. 3 8 6 16 24 Oktaedr + 2 tunely 3. 4 5 8 10 20 Krychle + 2 tunely 4. 3 9 4 12 18 Tetraedr + 2 tun. 5. 4 6 12 Krychle + 1 tunel 6. 5 5 4 4 10 Otevřené pentagonální těleso, duální samo k sobě 7. 6 4 12 duální k 5. 8. 9 3 12 4 18 duální k 4. 9. 5 4 10 8 20 duální k 3. 10. 8 3 16 6 24 duální k 2. 11. 7 3 28 12 42 duální k 1.

Domácí úkol - rozmyslet 1. Najděte nekonvexní mnohostěn, který nesplňuje Eulerův vztah. 2. Najděte nekonvexní mnohostěn, který splňuje Eulerův vztah. 3. Je dán konvexní čtrnáctistěn s devíti vrcholy. Dokažte, že na něm existuje vrchol, ze kterého vychází aspoň 5 hran. 4. Určete počty rovin souměrnosti všech Platonových těles. 5. Na kolik částí se rozpadnou, provedeme-li všechny tyto řezy současně? 6. Kolik prvků mají grupy zákrytových pohybů Platonových těles?

Literatura n Březina, F. a kol. : Stereochemie a některé fyzikálně chemické metody studia anorganických látek. UP, Olomouc 1994. n Huylebrouck, D. : Regular Polyhedral Lattices of Genus 2: 11 Platonic Equivalents? In: Bridges Conference Proceedings, Pécs 2010. n Molnár, J. , Kobza, J. : Extremálne a kombinatorické úlohy z geometrie. SPN, Bratislava 1991. Vacík, J. : Obecná chemie. SPN, Praha 1986. Vacík, J. a kol. : Přehled středoškolské chemie. SPN, Praha 1996. Zimák, J. : Mineralogie a petrografie. UP, Olomouc 1993 n n