Mean Delay in MG1 Queues with HeadofLine Priority

Mean Delay in M/G/1 Queues with Head-of-Line Priority Service and Embedded Markov Chains Wade Trappe

Lecture Overview l Priority Service – – – l Setup Mean Waiting Time for Type-1 Mean Waiting Time for Type-2 Generalization Summary Embedded Markov Chain Technique – Nk inside of N(t) – The queue distribution for M/G/1 u The PGF approach – Example: M/H 2/1 Queue – Homework: Alternate Pollaczek-Khinchine Derivation

M/G/1 Priority Services: Setup l Consider a queue that handles K priority classes of customers – Type-k customers arrive as a Poisson Process with rate l l and service times Customers are separated as they arrive and assigned to different “prio Each time the server is free: – Selects the next customer from highest priority, non-empty queue – This is the “head of line” service – We also assume that customers are not pre-empted! l Server Utilization for type-k customers is l Stability requirement:

Priority Services: Explanation 1 Queue-1 1 2 Server 2 Queue-2 Blue Type-1 Packets always have priority, but cannot preempt Type-2 packets

Priority Services: Mean Waiting Times l Our first goal will be to calculate the mean waiting time for Type-1 c l Assume a type-1 customer arrives and finds Nq 1(t)=k 1 type-1 already l Assume we use FCFS within each class l W 1 consists of: – Residual time R of customer in server – k 1 service times of type-1 in queue l Thus: l We get the mean waiting time for type-1 as

Priority Services: Mean Waiting Times, pg 2 l Now, let us look at a type-2 customer. When he arrives he may find – Nq 1(t)=k 1 type-1 already in the queue-1 – Nq 2(t)=k 2 type-2 already in the queue-2 Thus, W 2 is the sum of: – Residual service time R – k 1 service times for type-1 customers – k 2 service times for type-2 customers – AND service times of any new type-1 customers!!! l We get the mean waiting time for type-2 as l

Priority Services: Mean Waiting Times, pg 3 l Here, M 1 is the number of customers of type-1 that arrive during type l By Little’s Theorem applied to the queues: l The mean number of type-1 arrivals during l Substitute to get seconds is

Priority Services: Mean Waiting Times, pg 4 l Solve for : l Generalizing gives l Now, we’re left with finding E[R]!

Priority Services: Mean Waiting Times, pg 5 l When a customer arrives, the one being serviced can be of any type! l We will use the same formulation as where is the aggregate Poisson Process rate. l To get E[X 2] we use the fact that the fraction of type-k customers is l Thus, we get

Priority Services: Mean Delay l Now, calculating the mean delay for a type-k customer is easy! l From this, observe: – Class-k customers are affected by the behavior of lower priority c

Embedded Markov Chain Methods for M/G/1

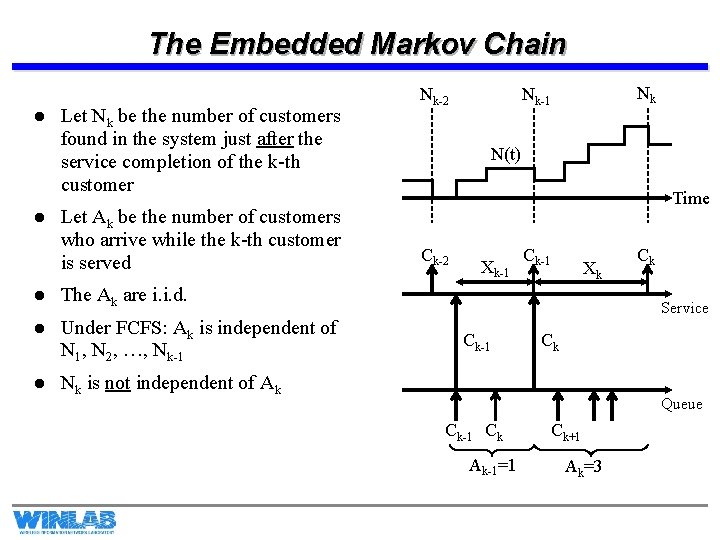
The Embedded Markov Chain l l Let Nk be the number of customers found in the system just after the service completion of the k-th customer Let Ak be the number of customers who arrive while the k-th customer is served l The Ak are i. i. d. l Under FCFS: Ak is independent of N 1, N 2, …, Nk-1 l Nk is not independent of Ak Nk-2 Nk Nk-1 N(t) Time Ck-2 Xk-1 Ck-1 Xk Ck Service Ck-1 Ck Queue Ck-1 Ck Ak-1=1 Ck+1 Ak=3

Embedded Markov Chain, pg 2 l We may find the following recursion: l Where did first line come from? – If l , then k-th customer finds the system empty, and on departure he The second line: – The queue left by the k-th customer consists of the previous queue decreased b l Let U(x)=1 for x>0 and U(x)=0 for x<=0 l Then we get

Embedded Markov Chain, pg 3 l From we can see that Nk is a Markov Chain since Nk depends on the past only l Nk is called the embedded Markov Chain l (Homework): The distribution for N(t) and Nk are the same: – Step 1: Show, in M/G/1, distributions found by arriving customer – Step 2: Show, in M/G/1, the distribution of customers found by ar l We will analyze Nk instead of N(t)

M/G/1 Queue Distribution l To find the queue distribution, we use the probability generating func l The PGF of the distribution {pn} is l Substitute l Thus and use independence to get

M/G/1 Queue Distribution, pg. 2 l If the service time of customer k is t, then Ak has a Poisson distributi l Now multiply by the f. X(t), the pdf of the service time Xk, This gives t l Integrate out X to obtain the unconditional pdf of Ak l What does this remind you of? l Answer: Laplace Transforms!!!

M/G/1 Queue Distribution, pg. 3 l The Probability Generating Function of Ak is given by Laplace Transform of f. X(t) l Substitute into earlier result to get:

M/G/1 Queue Distribution, pg. 4 l We need to now find p 0! l To do this, look at limit as z goes to 1, and apply L’Hopital… l First, go back to l Observe that P(z=1)=1, Ak(z=1)=1 l Thus l We used: Show This!

M/G/1 Queue Distribution, pg. 5 l Thus, l This is exactly what we got for M/M/1 Queues!!! l Substitute into earlier result to get: l What do we do with this? Use it to find the probability distribution pn l How? Equate terms… Best to see an example

M/H 2/1 Queue l Consider the case where FX(t), the cdf, is a two-term hyper-exponent l Where do hyper-exponentials come from? – In practice, from situations where service times can be represented as a mixture – That is, suppose there are k types of customers, each occuring with a probabilit – Customer of type I has a service time exponentially distributed with mean 1/mi l Then the density is

M/H 2/1 Queue, pg. 2 l Back to our 2 -phase hyper-exponential problem… l The mean service time is given by l The Laplace Transform of f. X(t) is: l We thus get:

M/H 2/1 Queue, pg. 3 l The PGF of {pn} is l The probability distribution is obtained through partial-fraction expa l To do this, we must find the roots of the denominator… call these z 1 l Then P(z) has the form: = Total Traffic Intensity

M/H 2/1 Queue, pg. 4 l Solving for C 1 and C 2 involves setting z=0 and z=1 to get l Finally, upon substitution, we get: