Mean Delay Optimization for the MG1 Queue with





- Slides: 10

Mean Delay Optimization for the M/G/1 Queue with Pareto Type Service Times Samuli Aalto TKK Helsinki University of Technology, Finland Urtzi Ayesta LAAS-CNRS, France aalto. ppt ACM Sigmetrics 2007, San Diego, CA, 12 -16 June 2007 1

Known optimality results for M/G/1 • Among all scheduling disciplines – SRPT (Shortest-Remaining-Processing-Time) optimal • minimizing the queue length process; thus, also the mean delay (i. e. sojourn time) • Among non-anticipating (i. e. blind) scheduling disciplines – FCFS (First-Come-First-Served) optimal for NBUE (New-Better-than-Used-in-Expectation) service times • minimizing the mean delay – FB (Foreground-Background) optimal for DHR (Decreasing-Hazard-Rate) service times • minimizing the mean delay • Definitions: – NBUE: E[S] ≥ E[S – x|S > x] for all x – DHR: hazard rate h(x) = f(x)/(1 -F(x)) decreasing for all x 2

Pareto service times • Pareto distribution – has a power-law (thus heavy) tail – has been used to model e. g. flow sizes in the Internet • Definition (type-1): h(x) – belongs to the class DHR – thus, FB optimal non-anticipating discipline • Definition (type-2): h(x) – does not belong to the class DHR – optimal non-anticipating discipline an open question. . . until now! 3

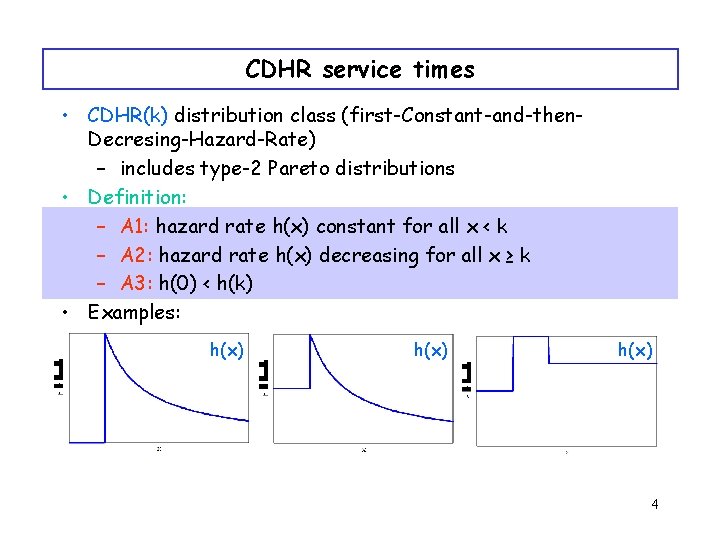
CDHR service times • CDHR(k) distribution class (first-Constant-and-then. Decresing-Hazard-Rate) – includes type-2 Pareto distributions • Definition: – A 1: hazard rate h(x) constant for all x < k – A 2: hazard rate h(x) decreasing for all x ≥ k – A 3: h(0) < h(k) • Examples: h(x) 4

Gittins index • Function J(a, ∆) for a job of age a and service quota ∆: – numerator: completion probability = ”payoff” – denominator: expected servicing time = ”investment” • Gittins index G(a) for a job of age a: • Original framework: – Multiarmed Bandit Problems [Gittins (1989)] 5

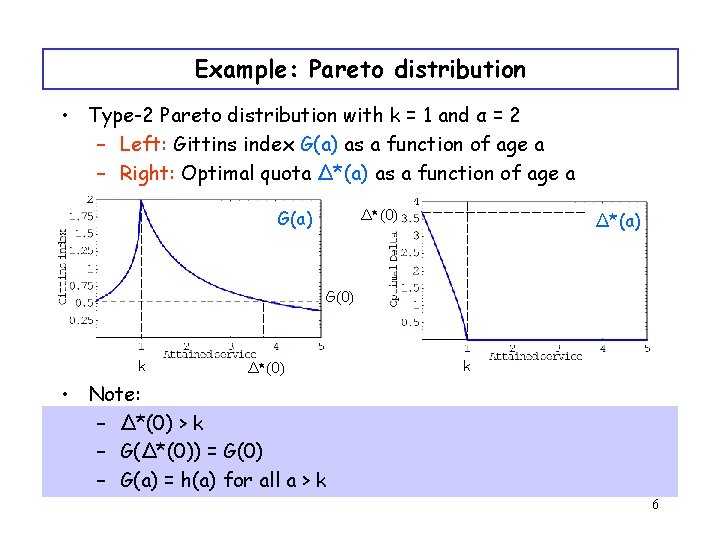
Example: Pareto distribution • Type-2 Pareto distribution with k = 1 and α = 2 – Left: Gittins index G(a) as a function of age a – Right: Optimal quota ∆*(a) as a function of age a Δ*(0) G(a) Δ*(a) G(0) k Δ*(0) k • Note: – ∆*(0) > k – G(∆*(0)) = G(0) – G(a) = h(a) for all a > k 6

Gittins discipline • Gittins discipline: – Serve the job with the highest Gittins index; if multiple, then PS among those jobs • Known result [Gittins (1989), Yashkov (1992)]: – Gittins discipline optimal among non-anticipating scheduling disciplines • minimizing the mean delay • Our New Result: – For CDHR service times (satisfying A 1 -A 3) the Gittins discipline (and thus optimal) is FCFS+FB(∆*(0)) • give priority for jobs younger than threshold ∆*(0) and apply FCFS among these priority jobs; • if no priority jobs, serve the youngest job in the system (according to FB) 7

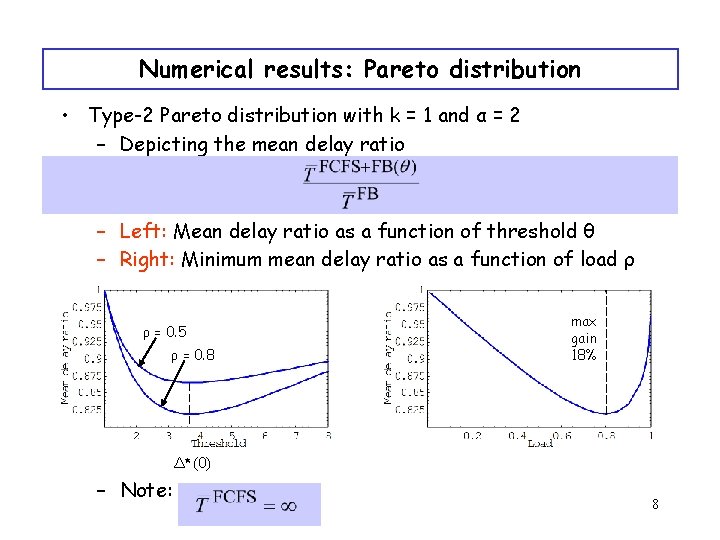
Numerical results: Pareto distribution • Type-2 Pareto distribution with k = 1 and α = 2 – Depicting the mean delay ratio – Left: Mean delay ratio as a function of threshold θ – Right: Minimum mean delay ratio as a function of load ρ ρ = 0. 5 ρ = 0. 8 max gain 18% Δ*(0) – Note: 8

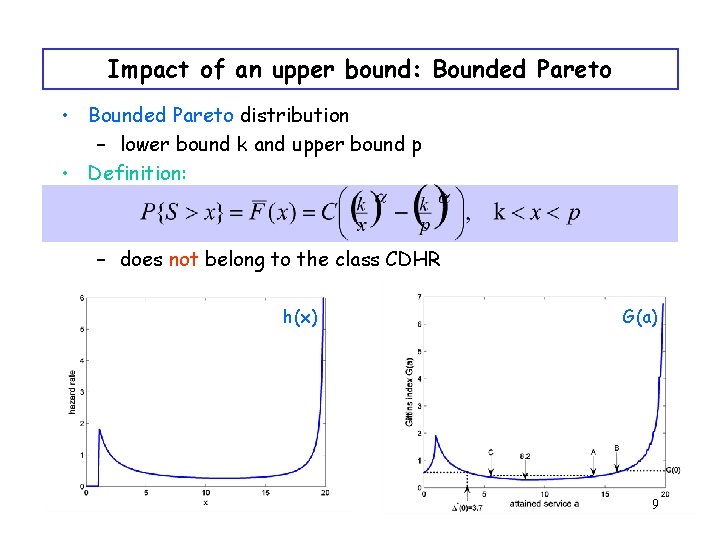
Impact of an upper bound: Bounded Pareto • Bounded Pareto distribution – lower bound k and upper bound p • Definition: – does not belong to the class CDHR h(x) G(a) 9

Conclusion and future research • Optimal non-anticipating scheduling studied for M/G/1 by applying the Gittins index approach • Observation: – Gittins index monotone iff the hazard rate monotone • Main result: – FCFS+FB(∆*(0)) optimal for CDHR service times • Possible further directions: – To generalize the result for IDHR service times – To apply the Gittins index approch • in multi-server systems or networks with the nonwork-conserving property • in wireless systems with randomly time-varing server capacity • in G/G/1 10 – To calculate performance metrics for a given G(a)