MATH 200 WEEK 3 MONDAY PLANES MATH 200

MATH 200 WEEK 3 - MONDAY PLANES

MATH 200 MAIN QUESTIONS FOR TODAY ▸ How do we describe planes in space? ▸ Can we find the equation of a plane that satisfies certain conditions? ▸ How do we find parametric equations for the line of intersection of two (non-parallel) planes? ▸ How do we find the (acute) angle of intersection between two planes.

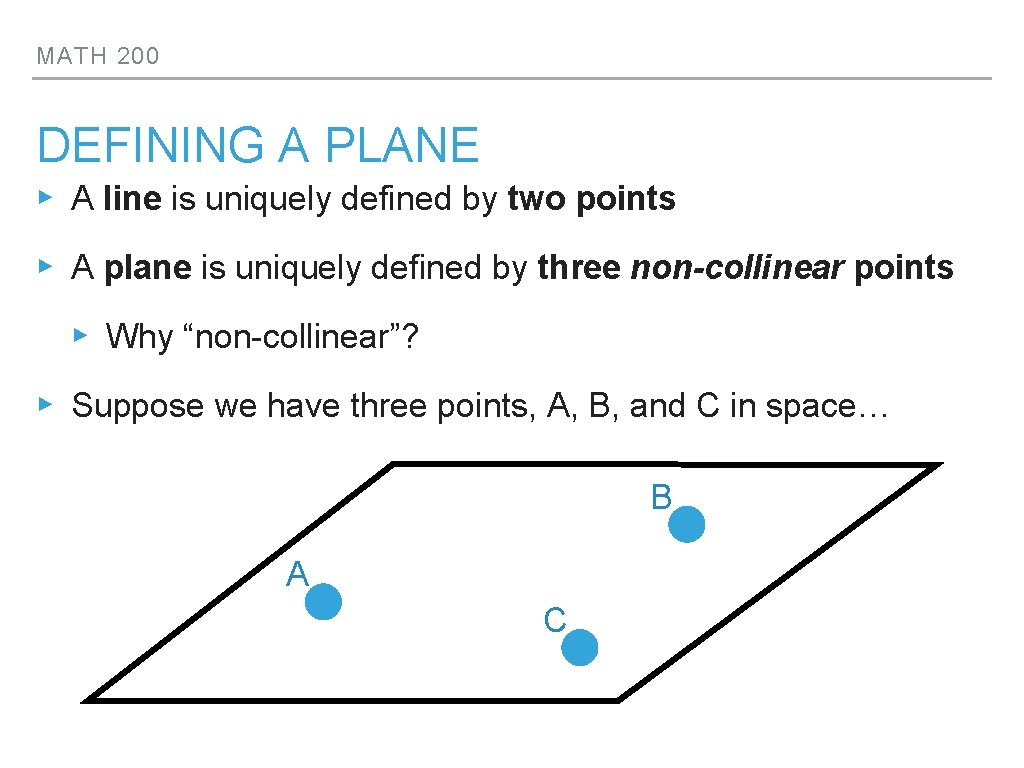
MATH 200 DEFINING A PLANE ▸ A line is uniquely defined by two points ▸ A plane is uniquely defined by three non-collinear points ▸ Why “non-collinear”? ▸ Suppose we have three points, A, B, and C in space… B A C

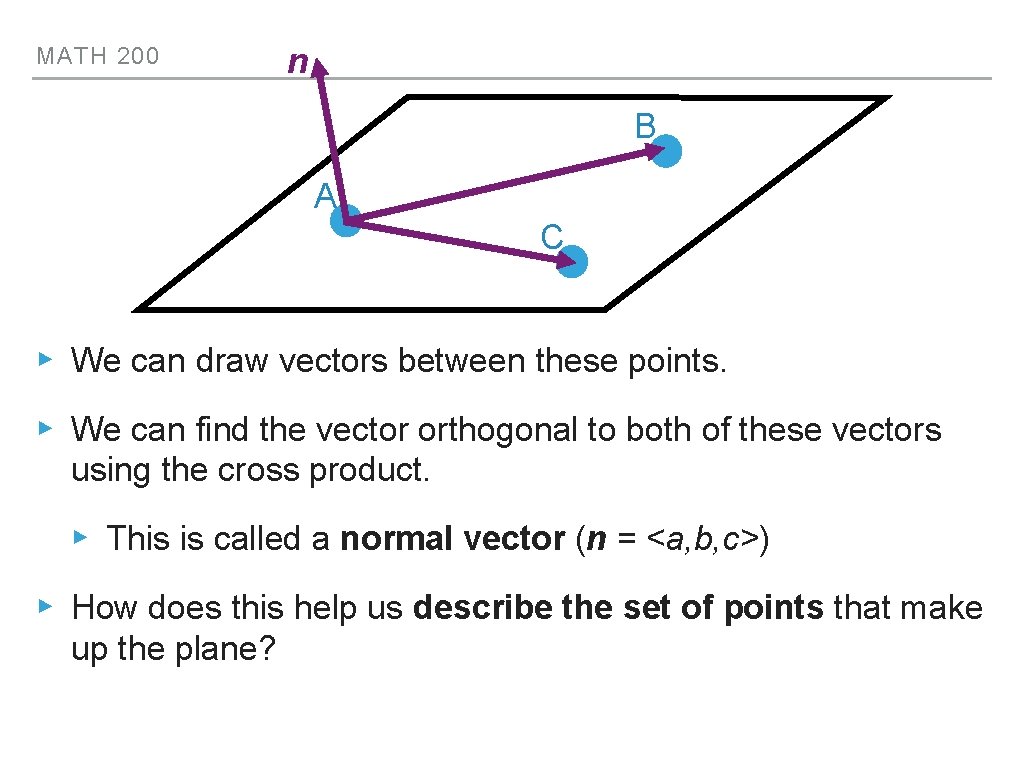
MATH 200 n B A C ▸ We can draw vectors between these points. ▸ We can find the vector orthogonal to both of these vectors using the cross product. ▸ This is called a normal vector (n = <a, b, c>) ▸ How does this help us describe the set of points that make up the plane?

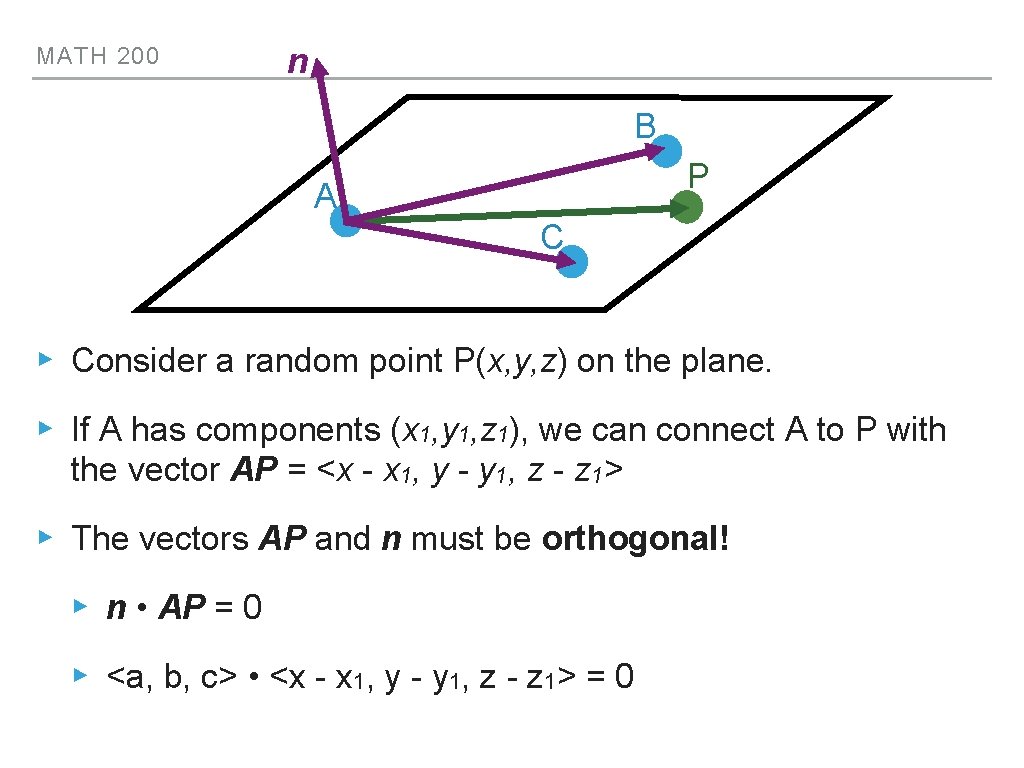
MATH 200 n B P A C ▸ Consider a random point P(x, y, z) on the plane. ▸ If A has components (x 1, y 1, z 1), we can connect A to P with the vector AP = <x - x 1, y - y 1, z - z 1> ▸ The vectors AP and n must be orthogonal! ▸ n • AP = 0 ▸ <a, b, c> • <x - x 1, y - y 1, z - z 1> = 0

MATH 200 FORMULA ▸ So, given a point (x 1, y 1, z 1) on a plane and a vector normal to the plane <a, b, c>, every point (x, y, z) on the plane must satisfy the equation ▸ We can also multiply this out: IS CALLED POINT-NORMAL FORM FOR A PL

MATH 200 FIND AN EQUATION FOR A PLANE ▸ Let’s find an equation for the plane that contains the following three points: n B ▸ A(1, 2, 1); B(3, -1, 2); C(-1, 0, 4) A ▸ We need the normal: n C ▸ n = AB x AC ▸ AB = <2, -3, 1> and AC = <-2, 3> ▸ n = AB x AC = <-7, -8, -10> ▸ Point-normal using A: -7(x-1) - 8(y-2) - 10(z-1) = 0

MATH 200 COMPARING ANSWERS ▸ Notice that we had three easy choices for an equation for the plane in the last example: ▸ Point-normal using A: -7(x-1) - 8(y-2) - 10(z-1) = 0 ▸ Point-normal using B: -7(x-3) - 8(y+1) - 10(z-2) = 0 ▸ Point-normal using C: -7(x+1) - 8 y - 10(z-4) = 0 ▸ We also could have scaled the normal vector we used: ▸ -14(x-1) - 16(y-2) - 20(z-1) = 0 ▸ This makes comparing our answers trickier ▸ To make comparing answers easier, we can put the equations into standard form

MATH 200 ▸ Standard form: ▸ ax + by + cz = d ▸ Multiply out point-normal form and combine constant terms on the right-hand side ▸ E. g. ▸ Point-normal using A: -7(x-1) - 8(y-2) - 10(z-1) = 0 ▸ -7 x + 7 - 8 y + 16 - 10 z + 10 = 0 ▸ -7 x - 8 y - 10 z = -33 or 7 x + 8 y + 10 z = 33 ▸ Point-normal using C: -7(x+1) - 8 y - 10(z-4) = 0 ▸ -7 x - 7 - 8 y - 10 z + 40 = 0 ▸ -7 x - 8 y - 10 z = -33 or 7 x + 8 y + 10 z = 33

MATH 200 EXAMPLE 1 ▸ Find an equation for the plane in standard form which contains the point A(-3, 2, 5) and is perpendicular to the line L(t)=<1, 4, 2>+t<3, -1, 2> ▸ Since the plane is perpendicular to the line L, its direction vector is normal to the plane. ▸ n = <3, -1, 2> ▸ Plane: 3(x+3) - (y-2) + 2(z-5) = 0 ▸ 3 x + 9 - y + 2 z - 10 = 0 ▸ 3 x - y + 2 z = -1

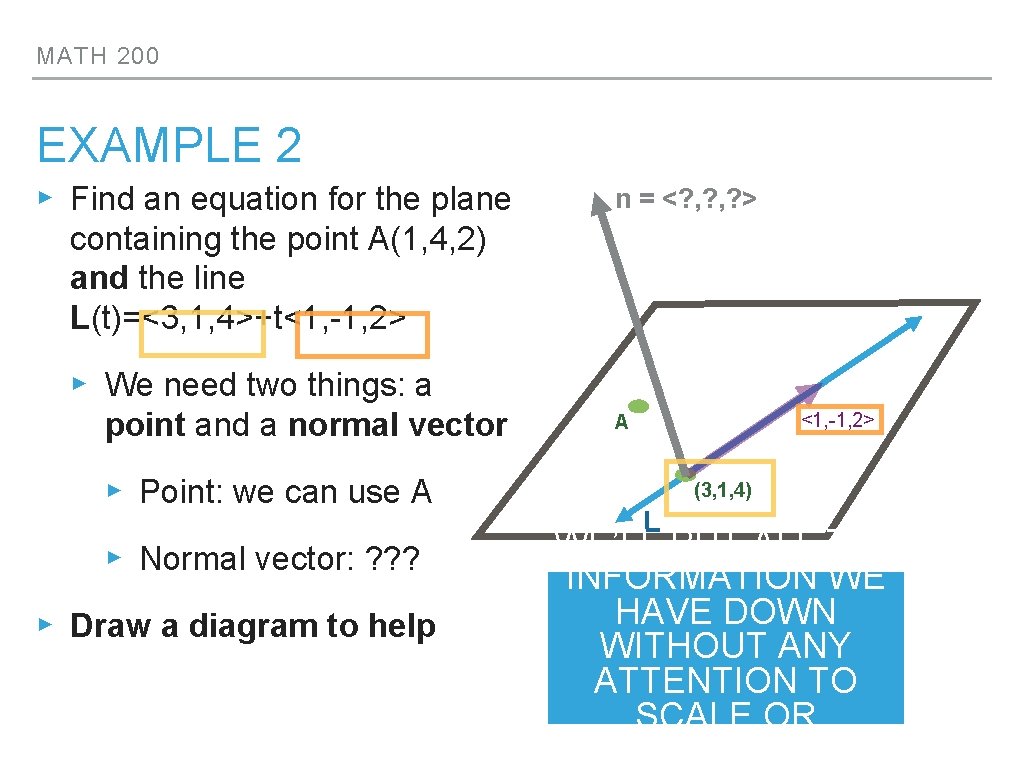
MATH 200 EXAMPLE 2 ▸ Find an equation for the plane n = <? , ? > containing the point A(1, 4, 2) and the line L(t)=<3, 1, 4>+t<1, -1, 2> ▸ We need two things: a point and a normal vector ▸ Point: we can use A ▸ Normal vector: ? ? ? ▸ Draw a diagram to help <1, -1, 2> A (3, 1, 4) L WE’LL PUT ALL THE INFORMATION WE HAVE DOWN WITHOUT ANY ATTENTION TO SCALE OR PROPORTION

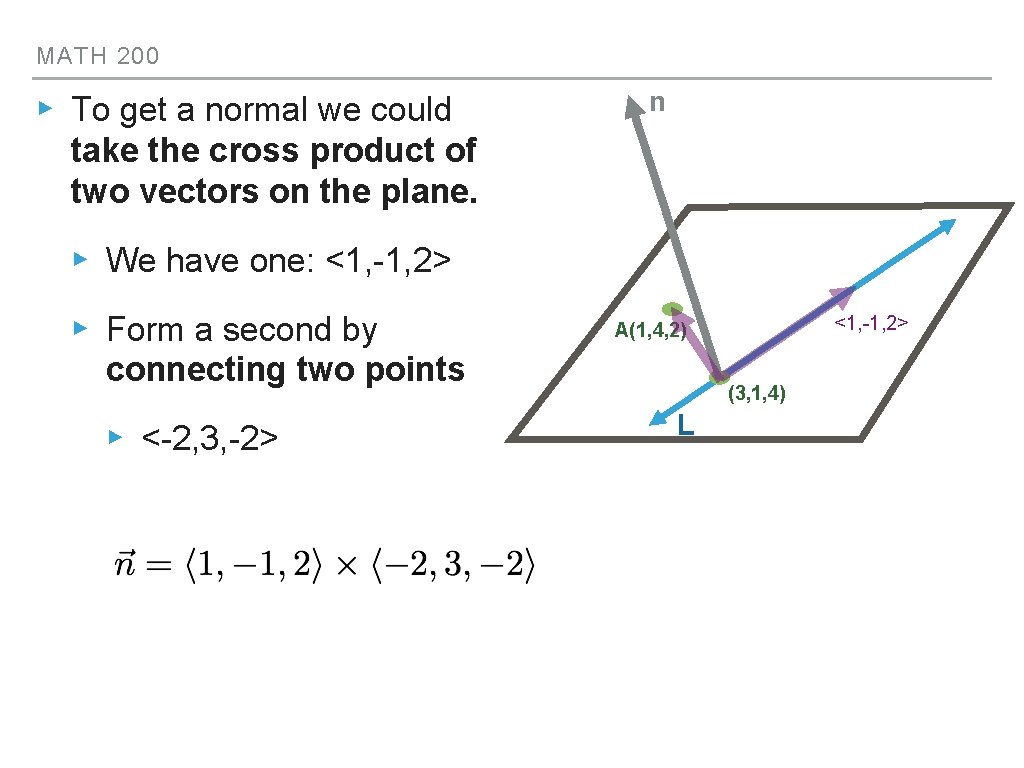
MATH 200 ▸ To get a normal we could n take the cross product of two vectors on the plane. ▸ We have one: <1, -1, 2> ▸ Form a second by connecting two points ▸ <-2, 3, -2> <1, -1, 2> A(1, 4, 2) (3, 1, 4) L

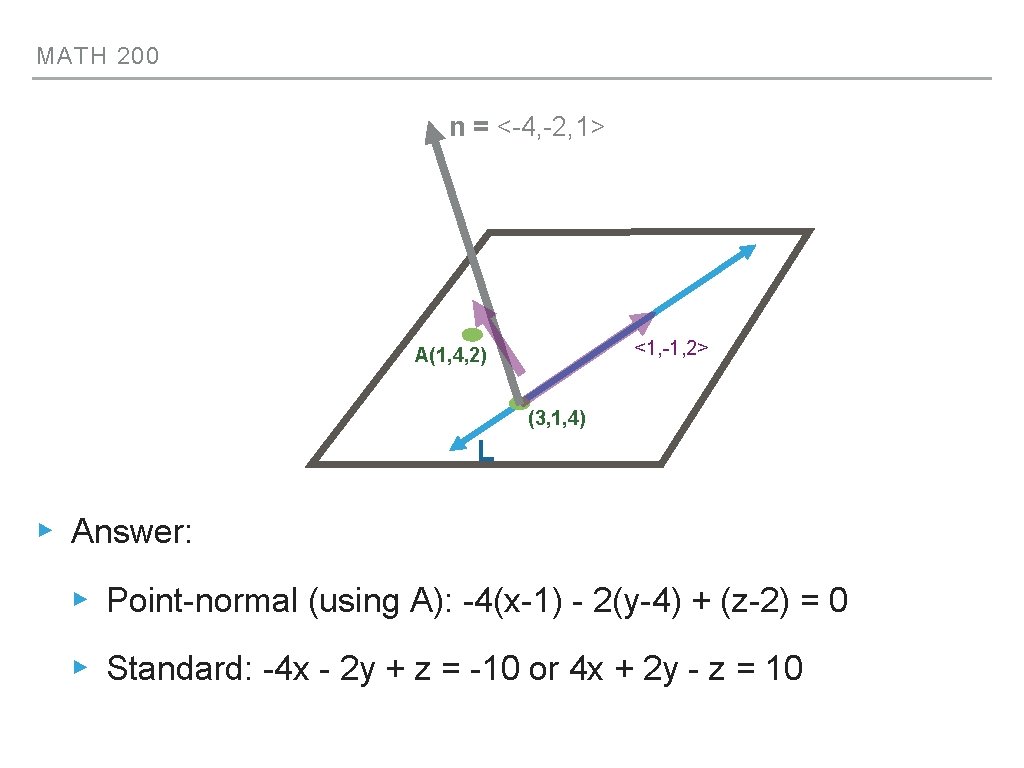
MATH 200 n = <-4, -2, 1> <1, -1, 2> A(1, 4, 2) (3, 1, 4) L ▸ Answer: ▸ Point-normal (using A): -4(x-1) - 2(y-4) + (z-2) = 0 ▸ Standard: -4 x - 2 y + z = -10 or 4 x + 2 y - z = 10

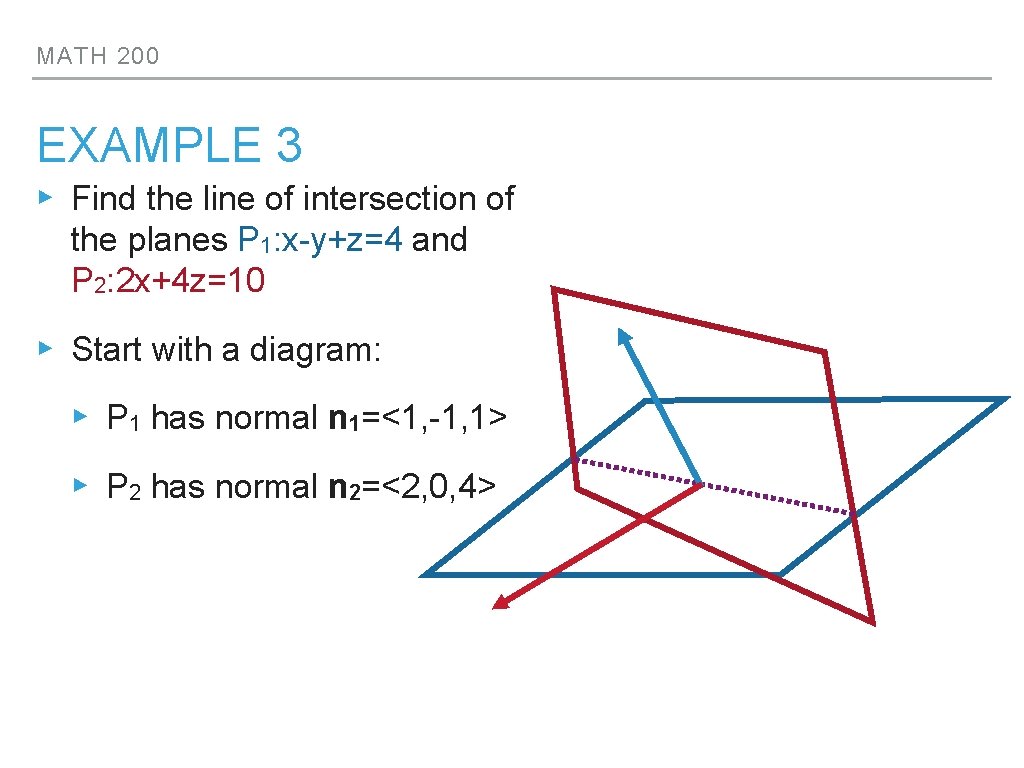
MATH 200 EXAMPLE 3 ▸ Find the line of intersection of the planes P 1: x-y+z=4 and P 2: 2 x+4 z=10 ▸ Start with a diagram: ▸ P 1 has normal n 1=<1, -1, 1> ▸ P 2 has normal n 2=<2, 0, 4>

MATH 200 ▸ Normal Vector: ▸ A vector parallel to the intersection will be orthogonal to both normal vectors. ▸ n = <1, -1, 1> x <2, 0, 4> = <-4, -2, 2> ▸ Point: ▸ a point in the intersection will satisfy both equations ▸ Because we have three variables and two equations, one variable is free - we can set one equal to a constant. ▸ Let z=0. Then we get ▸ x-y=4 and 2 x=10 ▸ So x = 5 and y = 1. ▸ Therefore, we have the point (5, 1, 0) common to both planes. ▸ Answer: L: <5, 1, 0> + t<-4, -2, 2>