MATH 200 WEEK 4 MONDAY FUNCTIONS OF SEVERAL

MATH 200 WEEK 4 - MONDAY FUNCTIONS OF SEVERAL

MATH 200 MAIN GOALS FOR TODAY ▸ Be able to describe and sketch the domain of a function of two or more variables ▸ Domains will be 2 D or 3 D regions ▸ Know how to evaluate a function of two or more variables ▸ Be able to compute and sketch level curves & surfaces ▸ These are just traces of the form z = k

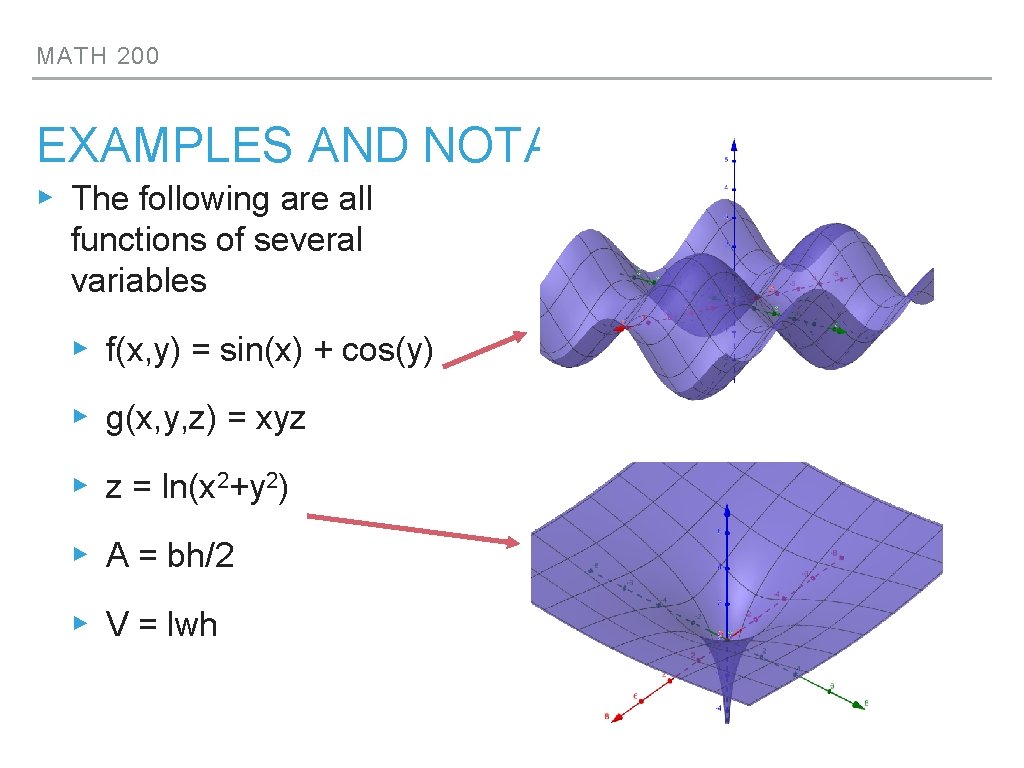
MATH 200 EXAMPLES AND NOTATION ▸ The following are all functions of several variables ▸ f(x, y) = sin(x) + cos(y) ▸ g(x, y, z) = xyz ▸ z = ln(x 2+y 2) ▸ A = bh/2 ▸ V = lwh

MATH 200 DEFINITIONS ▸ A function of two variables, x and y, is a rule that assigns to each ordered pair, (x, y), exactly one real number. ▸ We assign the value of f(x, y) to z to get a surface ▸ The domain of a function of two variables is the set of ordered pairs (x, y) for which f is defined ▸ A function of three variables, x, y, and z, is a rule that assigns to each ordered triple, (x, y, z), exactly one real number. ▸ The domain of a function of three variables is the set of ordered triples (x, y, z) for which f is defined

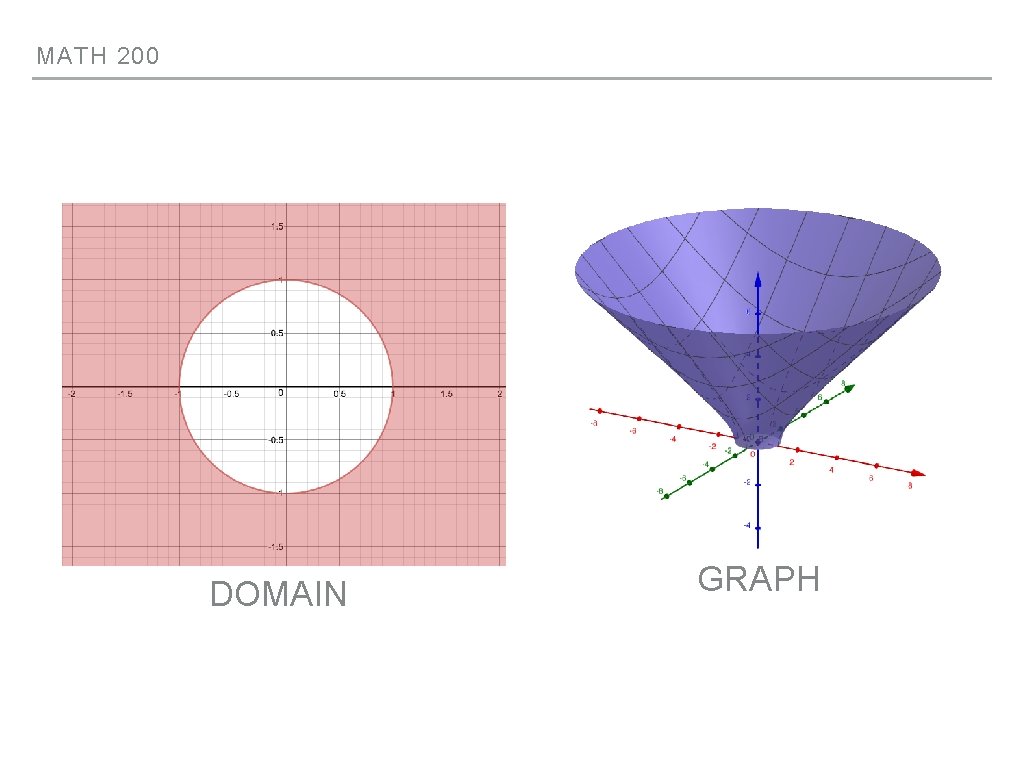
MATH 200 DOMAIN FOR A FUNCTION OF TWO ▸VARIABLES Consider the function f(x, y) = ln(1 -x 2 -y 2) ▸ We know that the input for ln() must be positive ▸ 1 - x 2 - y 2 > 0 ▸ x 2 + y 2 < 1 ▸ Let’s sketch the domain along with the graph of f

MATH 200 ONE MORE 2 -VARIABLE EXAMPLE ▸ Find and sketch the domain for the function ▸ We need the argument of the square root to be greater than or equal to zero ▸ x 2 + y 2 - 1 ≥ 0 ▸ x 2 + y 2 ≥ 1 ▸ All points on and outside the unit circle

MATH 200 DOMAIN GRAPH

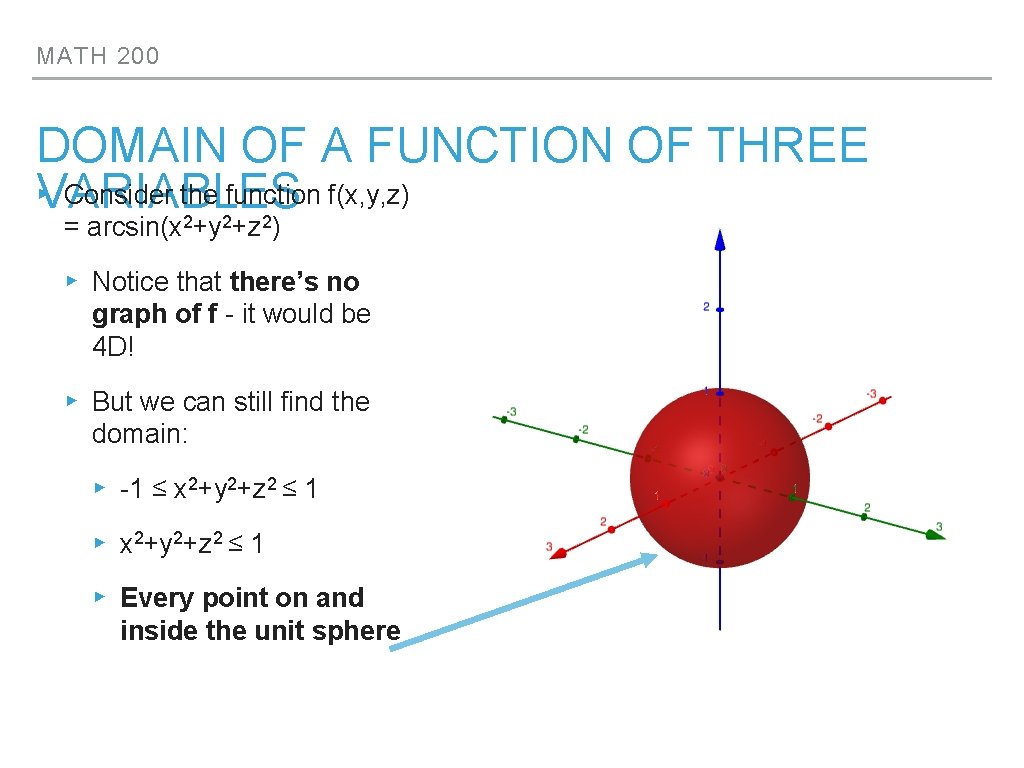
MATH 200 DOMAIN OF A FUNCTION OF THREE ▸VARIABLES Consider the function f(x, y, z) = arcsin(x 2+y 2+z 2) ▸ Notice that there’s no graph of f - it would be 4 D! ▸ But we can still find the domain: ▸ -1 ≤ x 2+y 2+z 2 ≤ 1 ▸ Every point on and inside the unit sphere

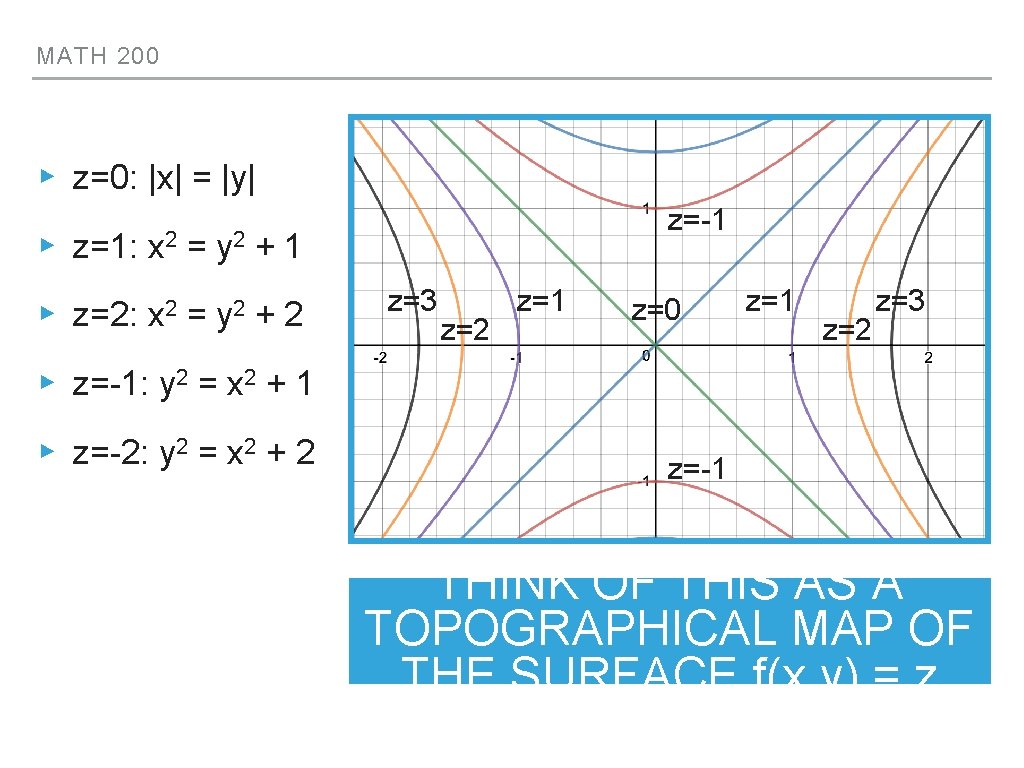
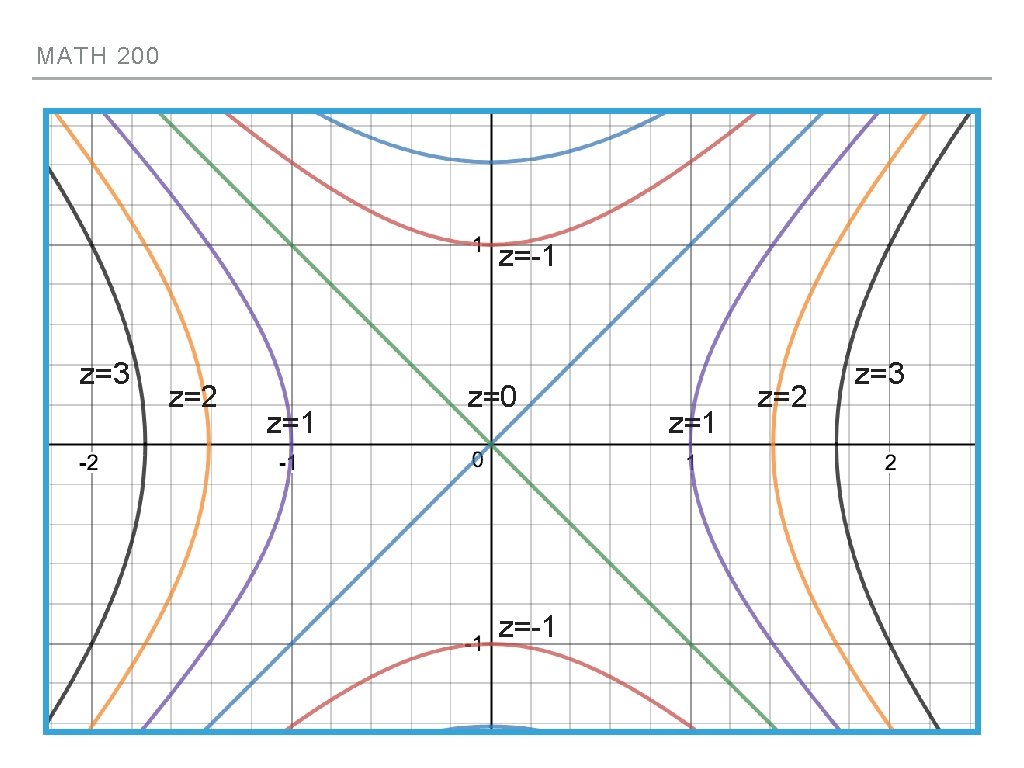
MATH 200 LEVEL CURVES AND CONTOUR PLOTS ▸(OR A level curve for a function CONTOUR MAPS)▸ z=0: 0 = x 2 - y 2 f(x, y) is a trace of the form z=constant ▸ It’s often useful to graph and label several level curves together on one set of axes ▸ We call this a contour plot ▸ E. g. consider the function z=x 2 -y 2 ▸ x 2 = y 2 ▸ |x| = |y| ▸ z=1: 1 = x 2 - y 2 ▸ x 2 = y 2 + 1 ▸ z=2: x 2 = y 2 + 2 ▸ z=-1: y 2 = x 2 + 1 ▸ z=-2: y 2 = x 2 + 2

MATH 200 ▸ z=0: |x| = |y| z=-1 ▸ z=1: x 2 = y 2 + 1 ▸ z=2: x 2 = y 2 +2 z=3 z=2 z=1 z=0 z=1 z=2 z=3 ▸ z=-1: y 2 = x 2 + 1 ▸ z=-2: y 2 = x 2 + 2 z=-1 THINK OF THIS AS A TOPOGRAPHICAL MAP OF THE SURFACE f(x, y) = z

MATH 200

MATH 200 z=-1 z=3 z=2 z=1 z=0 z=-1 z=2 z=3

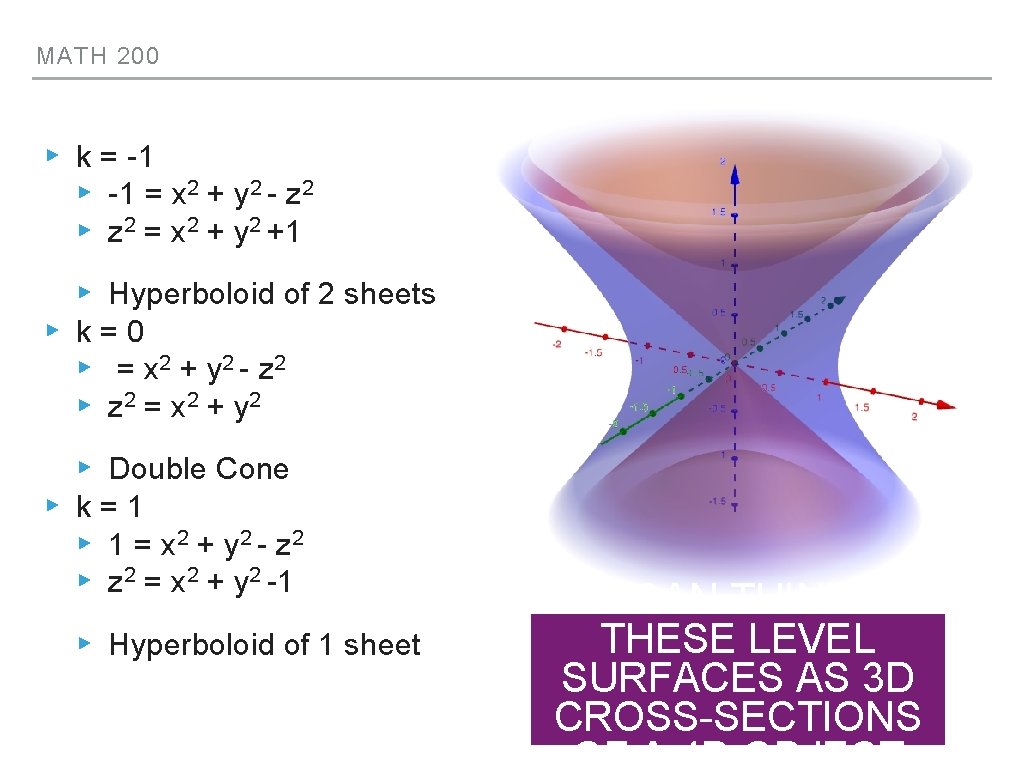
MATH 200 LEVEL SURFACES ▸ While we can’t graph functions of three variables, we can plot their level surfaces ▸ Level surfaces: given f(x, y, z), setting the function equal to a constant yields a level surface ▸ E. g. consider the function f(x, y, z) = x 2 + y 2 - z 2 ▸ Set f(x, y, z) = k (const. ) ▸ k = -1 ▸ -1 = x 2 + y 2 - z 2 ▸ z 2 = x 2 + y 2 +1 ▸ Hyperboloid of 2 sheets ▸ k=0 ▸ = x 2 + y 2 - z 2 ▸ z 2 = x 2 + y 2 ▸ Double Cone ▸ k=1 ▸ 1 = x 2 + y 2 - z 2 ▸ z 2 = x 2 + y 2 -1 ▸ Hyperboloid of 1 sheet

MATH 200 ▸ k = -1 ▸ -1 = x 2 + y 2 - z 2 ▸ z 2 = x 2 + y 2 +1 ▸ Hyperboloid of 2 sheets ▸ k=0 ▸ = x 2 + y 2 - z 2 ▸ z 2 = x 2 + y 2 ▸ Double Cone ▸ k=1 ▸ 1 = x 2 + y 2 - z 2 ▸ z 2 = x 2 + y 2 -1 ▸ Hyperboloid of 1 sheet WE CAN THINK OF THESE LEVEL SURFACES AS 3 D CROSS-SECTIONS