MATH 200 WEEK 1 WEDNESDAY VECTORS MATH 200

MATH 200 WEEK 1 - WEDNESDAY VECTORS

MATH 200 MAIN QUESTIONS FOR TODAY ▸ What is a vector? ▸ What operations can we do with vectors? ▸ What kinds of representations and notations do we have for vectors? ▸ What are some of the important properties of vectors?

MATH 200 DEFINITION ▸ A vector is a mathematical object with magnitude and direction. ▸ Representation: arrow whose length corresponds to magnitude ▸ Notation: ▸ Bold letters - e. g. v as opposed to v ▸ Arrow over letter:

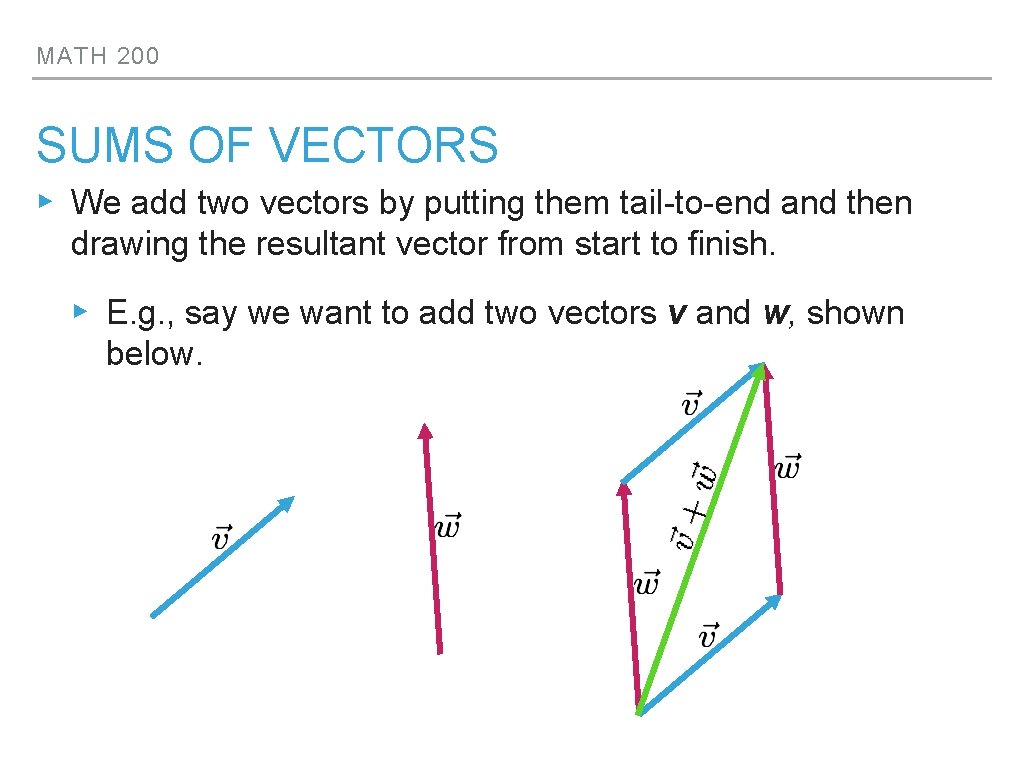
MATH 200 SUMS OF VECTORS ▸ We add two vectors by putting them tail-to-end and then drawing the resultant vector from start to finish. ▸ E. g. , say we want to add two vectors v and w, shown below.

MATH 200 ¡¡IMPORTANT!! THESE ARE ALL THE SAME BECAUSE THEY HAVE THE SAME DIRECTION AND MAGNITUDE ▸ VECTORS DO NOT HAVE FIXED POSITION!

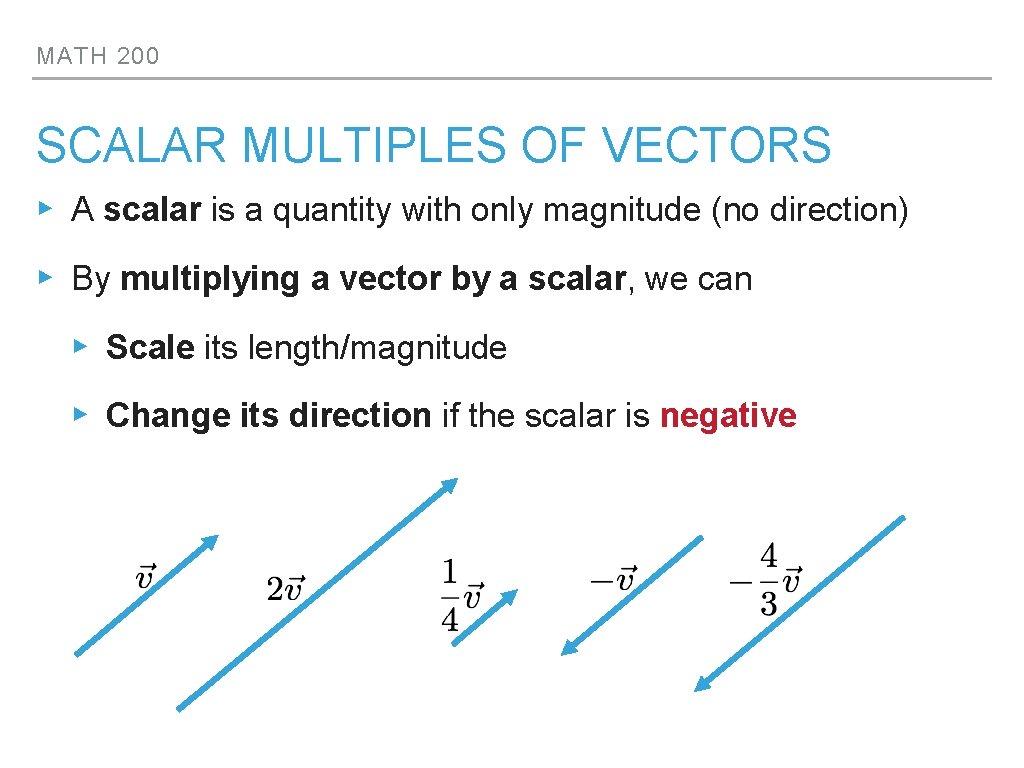
MATH 200 SCALAR MULTIPLES OF VECTORS ▸ A scalar is a quantity with only magnitude (no direction) ▸ By multiplying a vector by a scalar, we can ▸ Scale its length/magnitude ▸ Change its direction if the scalar is negative

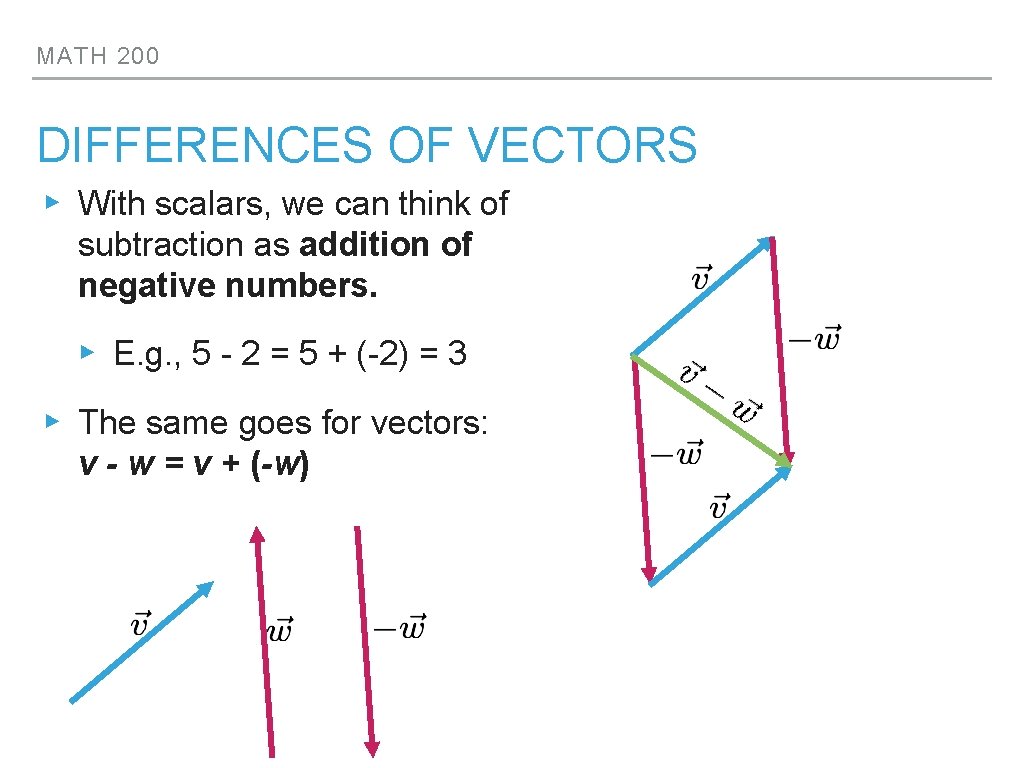
MATH 200 DIFFERENCES OF VECTORS ▸ With scalars, we can think of subtraction as addition of negative numbers. ▸ E. g. , 5 - 2 = 5 + (-2) = 3 ▸ The same goes for vectors: v - w = v + (-w)

MATH 200 VECTORS IN RECTANGULAR COORDINATES ▸ Suppose I draw a vector from one point to another. Call these points P 1(x 1, y 1, z 1) and P 2(x 2, y 2, z 2) P 2 ▸ We’ll write this vector in the following way: P 1

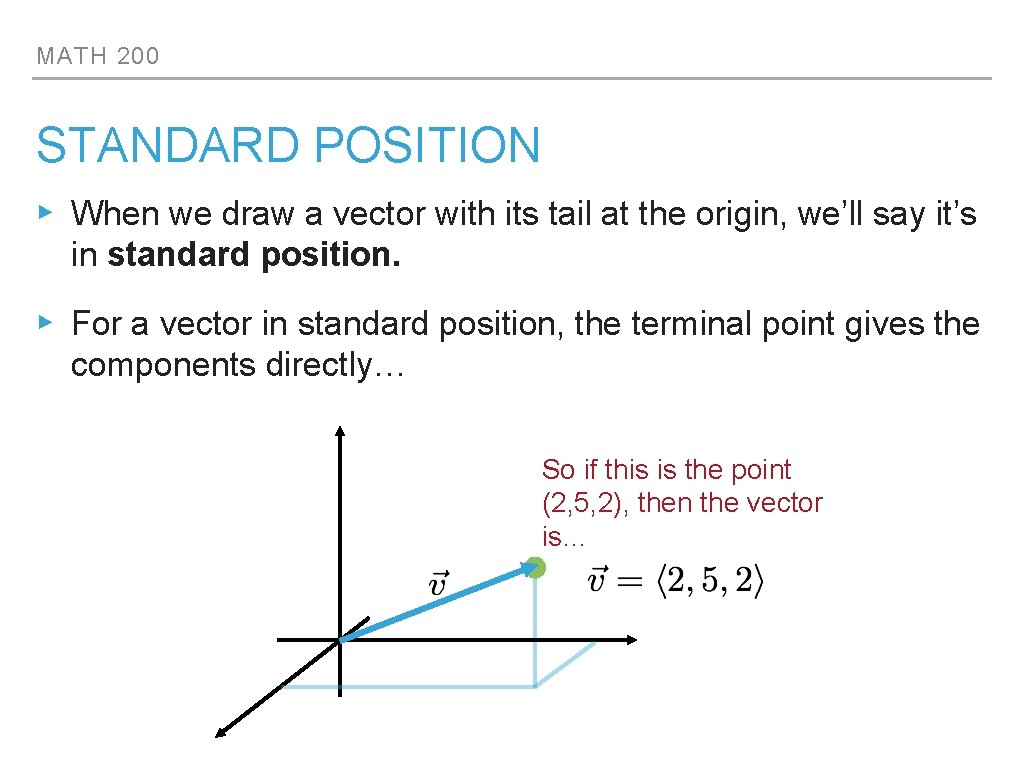
MATH 200 STANDARD POSITION ▸ When we draw a vector with its tail at the origin, we’ll say it’s in standard position. ▸ For a vector in standard position, the terminal point gives the components directly… So if this is the point (2, 5, 2), then the vector is…

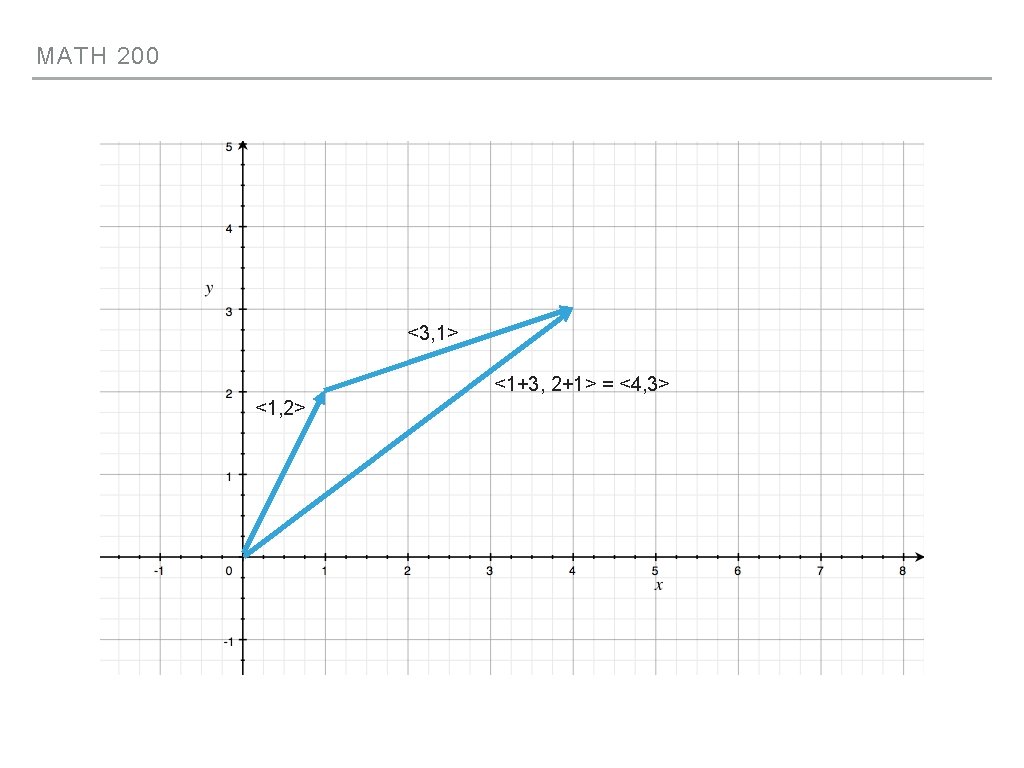
MATH 200 A 2 D EXAMPLE ▸ Do the following: ▸ Draw and label x and y axes ▸ Pick two vectors (e. g. v = <1, 2> and w = <-3, 1>) ▸ Draw v with its tail at the origin ▸ Draw w with its tail at the terminal point of v ▸ Draw v + w

MATH 200 <3, 1> <1+3, 2+1> = <4, 3> <1, 2>

MATH 200 PROPERTIES Vector operations work pretty much the way we’d like!

MATH 200 PARALLEL VECTORS ▸ We saw that scalar multiplication always gives us a parallel vector to the original. ▸ E. g. If v = <1, 2, -4>. ▸ Then 2 v = <2, 4, -8> and -3 v = <-3, -6, 12> are both parallel to v ▸ Conversely, we can say that two vectors are parallel if they are scalar multiples of one another! ▸ E. g. v = <1, 3, 1> and w = <-4, -12, -4> are parallel because w = -4 v ▸ Non-example: v = <1, 3, 1> and q = <2, 6, 4> are not parallel. ▸ How do we know? q 1 = 2 v 1 but q 3 = 4 v 3

MATH 200 NORM OF A VECTOR ▸ The norm of a vector is just its magnitude/length. ▸ We write ||v|| for the “norm of v” ▸ Since vectors don’t have a fixed position, we can put any vector in standard position and use those components in the distance formula: ▸ E. g. ,

MATH 200 ▸ What can we say about ||kv||? ▸ We know that k scales the magnitude of v ▸ We also know that if k is negative, we flip the direction of v ▸ Let’s see if that intuition corresponds to the algebra:

MATH 200 UNIT VECTORS ▸ When a vector has length one, we call it a unit vector ▸ Later, we’ll use unit vectors to define something called the directional derivative ▸ Often, we’ll need to take a non-unit vector, and shrink it to unit length ▸ This is called normalizing a vector

MATH 200 NORMALIZING VECTORS ▸ Suppose we want a vector in the same direction as a vector v = <2, -1, 1>, but with length one. ▸ We know that scalar multiplication by a positive number preserves direction. ▸ Let’s multiply v by 1/||v||

MATH 200 THREE SPECIAL UNIT VECTORS ▸ The three simplest unit vectors: <1, 0, 0>, <0, 1, 0>, <0, 0, 1> ▸ These get special names: ▸ i = <1, 0, 0> ▸ j = <0, 1, 0> ▸ k = <0, 0, 1> ▸ An alternative notation for vectors uses i, j, k: ▸ E. g. , <2, 3, 6> = 2 i + 3 j + 6 k And sometimes they get hats

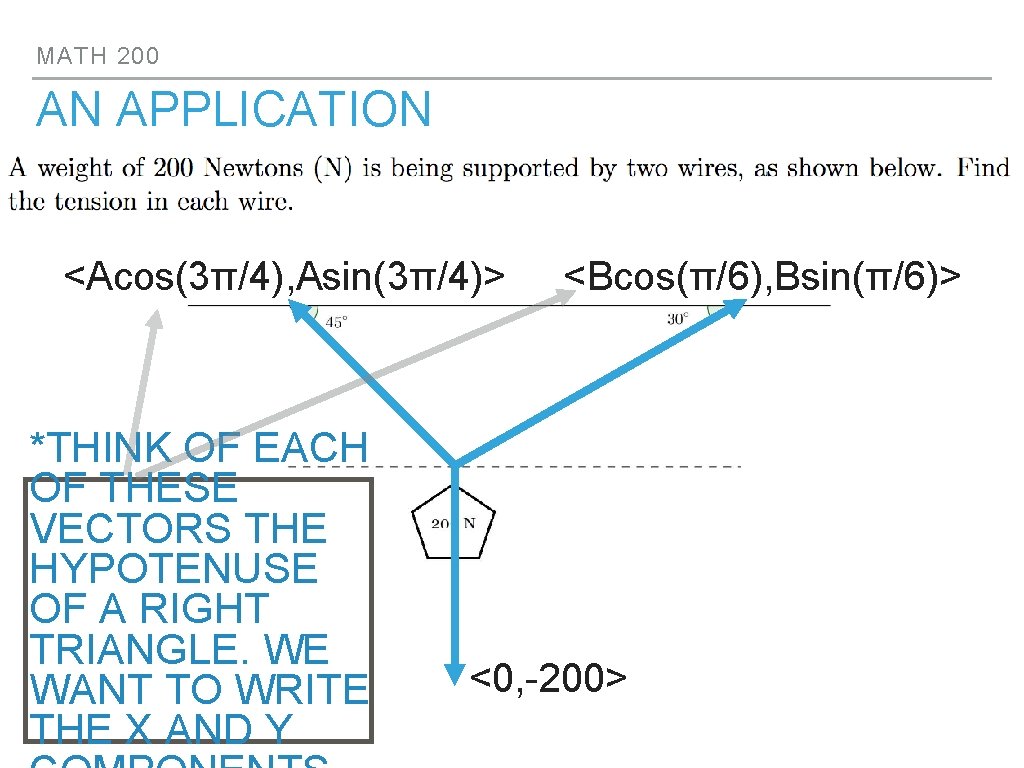
MATH 200 AN APPLICATION <Acos(3π/4), Asin(3π/4)> *THINK OF EACH OF THESE VECTORS THE HYPOTENUSE OF A RIGHT TRIANGLE. WE WANT TO WRITE THE X AND Y <Bcos(π/6), Bsin(π/6)> <0, -200>

MATH 200 ▸ If the weight isn’t moving, the three force vectors should add up to <0, 0> ▸ If two vectors are equal, they must have the same components.

MATH 200 Elimination Substitution