MATH 200 WEEK 3 FRIDAY QUADRIC MATH 200

MATH 200 WEEK 3 - FRIDAY QUADRIC

MATH 200 MAIN QUESTIONS FOR TODAY ▸ What are some of the main quadric surfaces? ▸ How do we distinguish between the various quadric surfaces? ▸ What is a trace? ▸ Given an equation in x, y, and z, how do we use traces to determine what the surface corresponding to the equation looks like?

MATH 200 QUADRIC SURFACES ▸ Surfaces that result from equations of the form ▸ Examples:

MATH 200 TRACES ▸ To figure out what these look like, we’ll start by looking at traces. ▸ A trace of a surface is the intersection of the surface with a given plane ▸ This will be a curve, a point, or nothing ▸ Putting traces together, we’ll deduce what the whole surface looks like ▸ Often, traces on planes like x=0, 1, 2, 3, …, y=0, 1, 2, 3…, and z=0, 1, 2, 3… will be enough

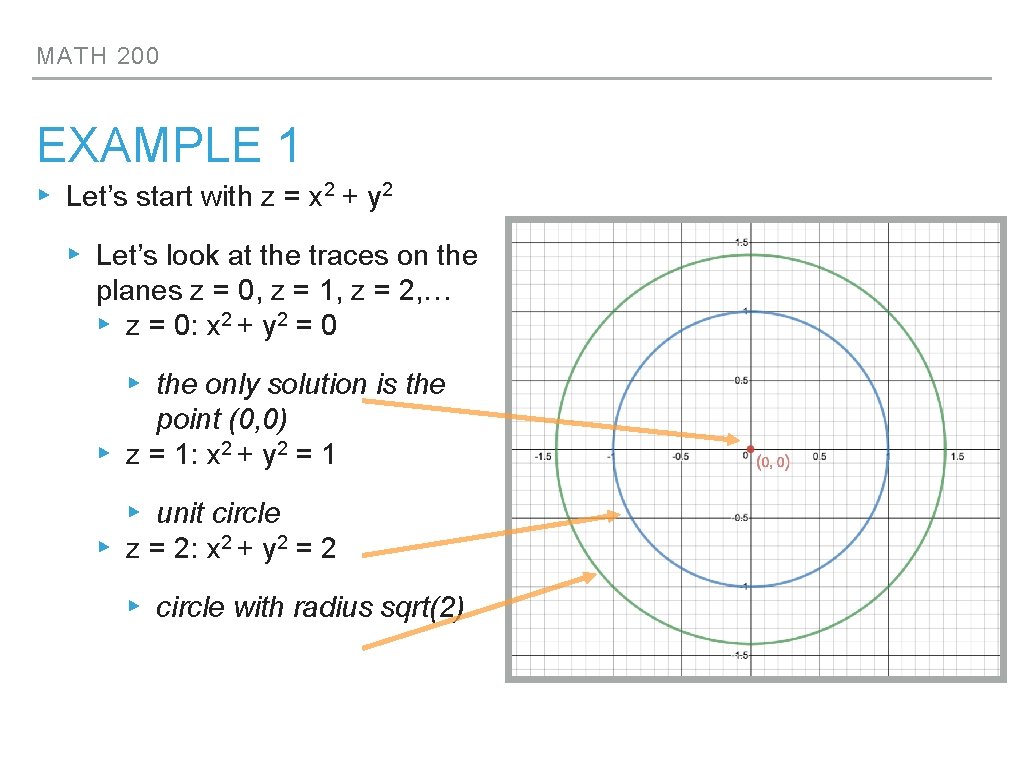
MATH 200 EXAMPLE 1 ▸ Let’s start with z = x 2 + y 2 ▸ Let’s look at the traces on the planes z = 0, z = 1, z = 2, … ▸ z = 0: x 2 + y 2 = 0 ▸ the only solution is the point (0, 0) ▸ z = 1: x 2 + y 2 = 1 ▸ unit circle ▸ z = 2: x 2 + y 2 = 2 ▸ circle with radius sqrt(2)

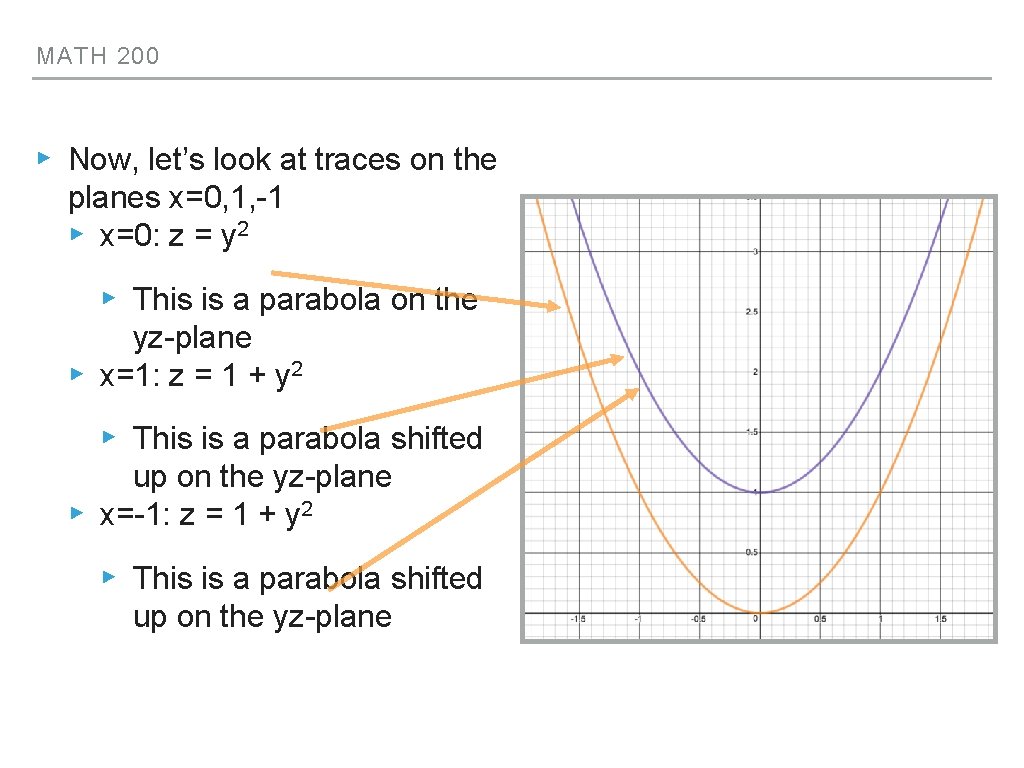
MATH 200 ▸ Now, let’s look at traces on the planes x=0, 1, -1 ▸ x=0: z = y 2 ▸ This is a parabola on the yz-plane ▸ x=1: z = 1 + y 2 ▸ This is a parabola shifted up on the yz-plane ▸ x=-1: z = 1 + y 2 ▸ This is a parabola shifted up on the yz-plane

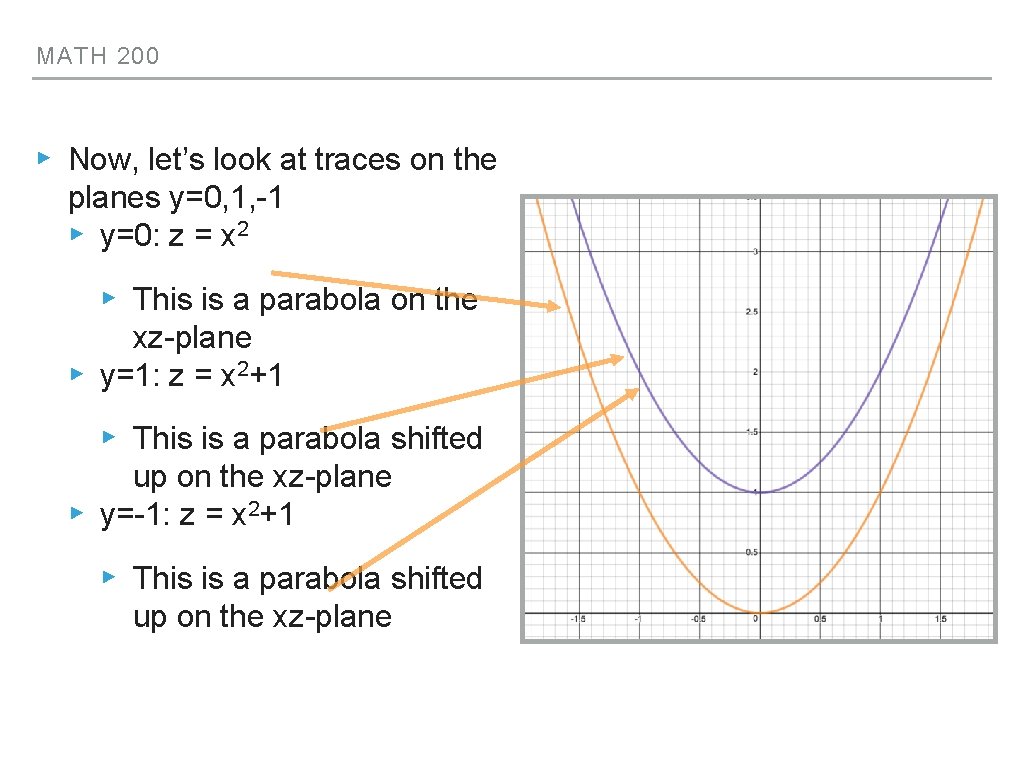
MATH 200 ▸ Now, let’s look at traces on the planes y=0, 1, -1 ▸ y=0: z = x 2 ▸ This is a parabola on the xz-plane ▸ y=1: z = x 2+1 ▸ This is a parabola shifted up on the xz-plane ▸ y=-1: z = x 2+1 ▸ This is a parabola shifted up on the xz-plane

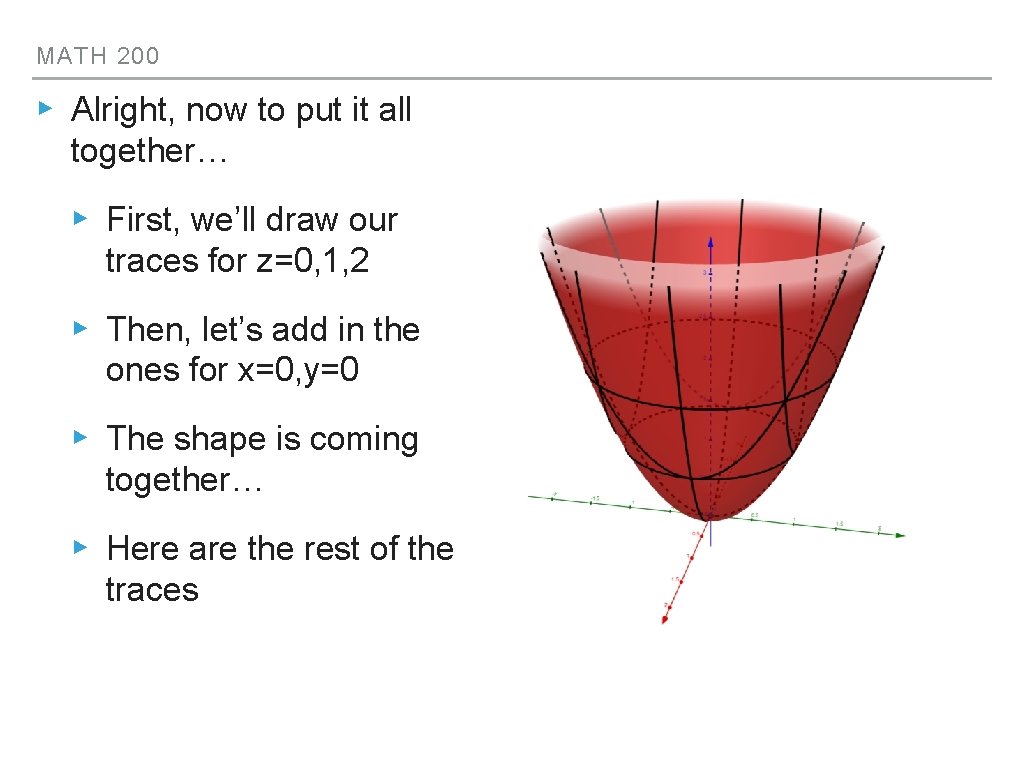
MATH 200 ▸ Alright, now to put it all together… ▸ First, we’ll draw our traces for z=0, 1, 2 ▸ Then, let’s add in the ones for x=0, y=0 ▸ The shape is coming together… ▸ Here are the rest of the traces

MATH 200 EXAMPLE 2 ▸ Let’s repeat the same process for z 2 = x 2 + y 2 ▸ Draw traces by setting x, y, and z equal to various constant values (e. g. -1, 1, 0, 1, 1) ▸ First draw those traces in 2 D ▸ Then combine them into a 3 D sketch ▸ With a few traces in each “direction” you should be able to deduce the shape…

MATH 200 ▸ Traces ▸ z = constant ▸ z = 0: 0 = x 2+y 2 (only a point (0, 0)) ▸ z = -1, 1 both give the same trace: 1 = x 2+y 2 (unit circle) ▸ x = constant ▸ x=0: z 2 = y 2, which is the same as |z| = |y| ▸ x = -1, 1 both give the same trace: z 2 = 1+y 2 (hyperbola) ▸ y = constant ▸ y=0: z 2 = x 2, which is the same as |z| = |x| ▸ y = -1, 1 both give the same trace: z 2 = x 2 + 1 (hyperbola)

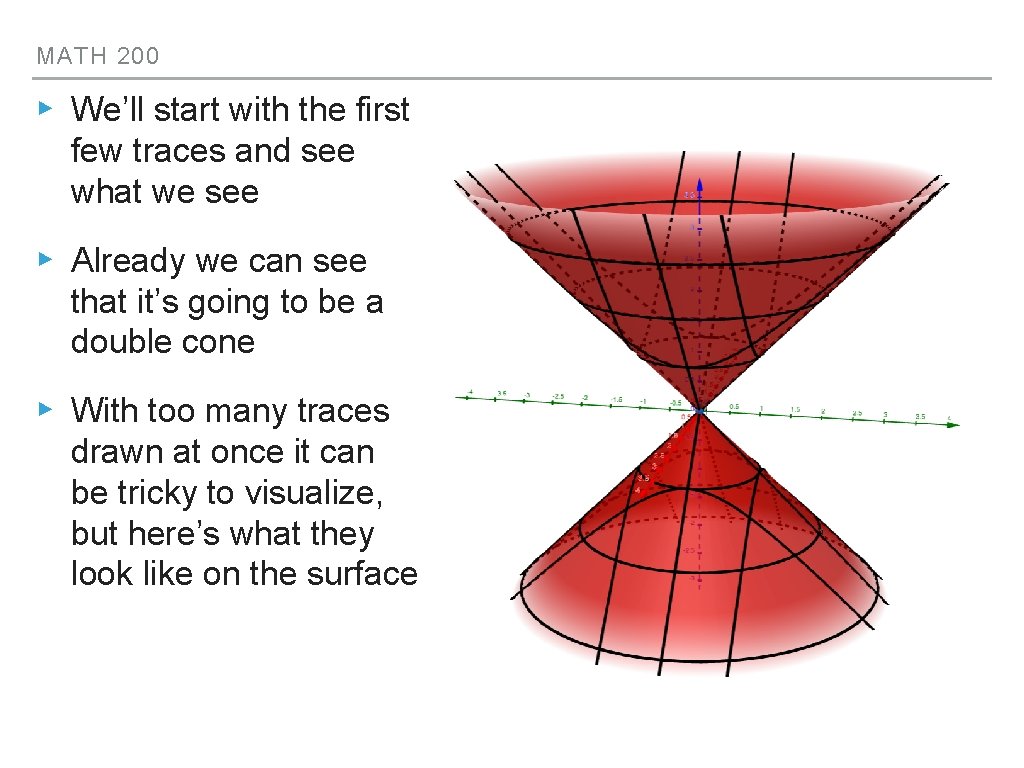
MATH 200 ▸ We’ll start with the first few traces and see what we see ▸ Already we can see that it’s going to be a double cone ▸ With too many traces drawn at once it can be tricky to visualize, but here’s what they look like on the surface

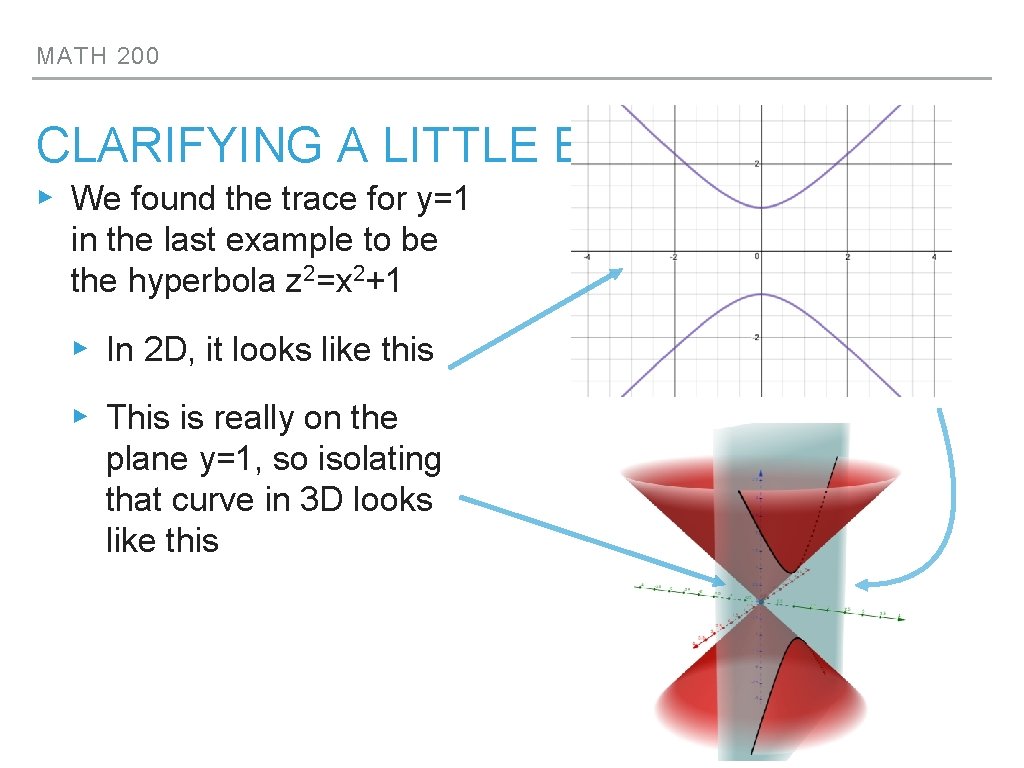
MATH 200 CLARIFYING A LITTLE BIT ▸ We found the trace for y=1 in the last example to be the hyperbola z 2=x 2+1 ▸ In 2 D, it looks like this ▸ This is really on the plane y=1, so isolating that curve in 3 D looks like this

MATH 200 EXAMPLE 3 ▸ Looking at z 2=x 2+y 2+1, we can tell one thing right away about the possible z-values… ▸ x 2+y 2+1 ≥ 1 which means z 2≥ 1 ▸ …which means z≤-1 and z≥ 1 ▸ …which means there’s an empty space between -1 and 1 in the z-direction ▸ Draw some traces for (valid) constant values of z ▸ Draw traces for x=0 and y=0 ▸ See if that’s enough…

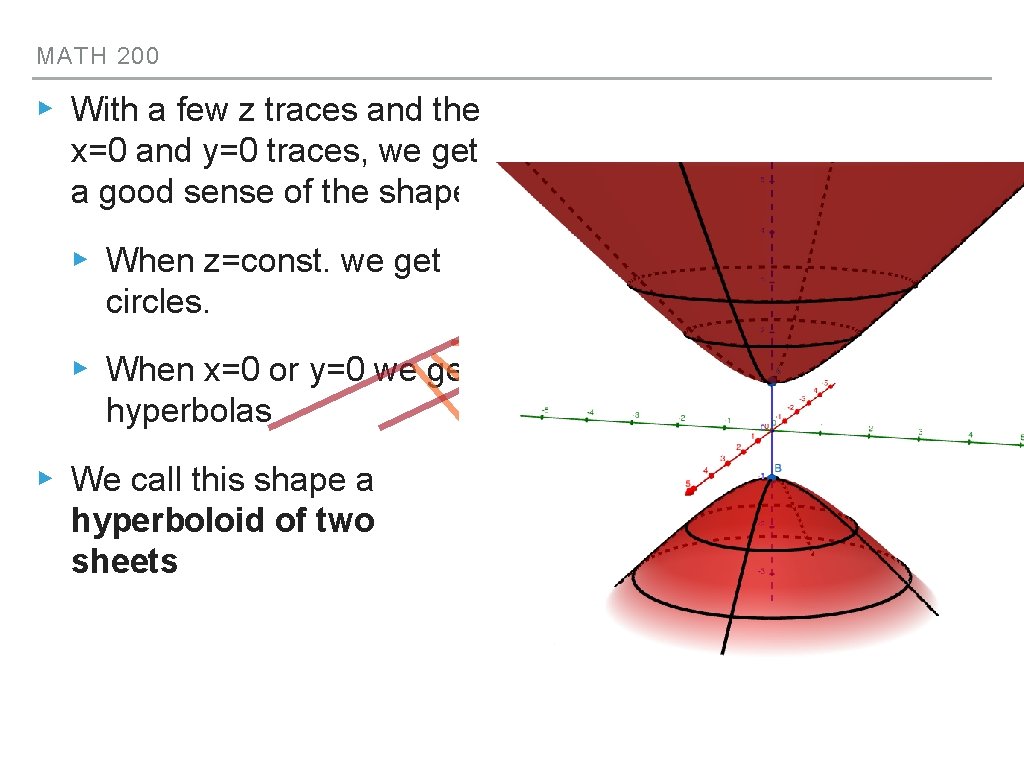
MATH 200 ▸ With a few z traces and the x=0 and y=0 traces, we get a good sense of the shape ▸ When z=const. we get circles. ▸ When x=0 or y=0 we get hyperbolas ▸ We call this shape a hyperboloid of two sheets

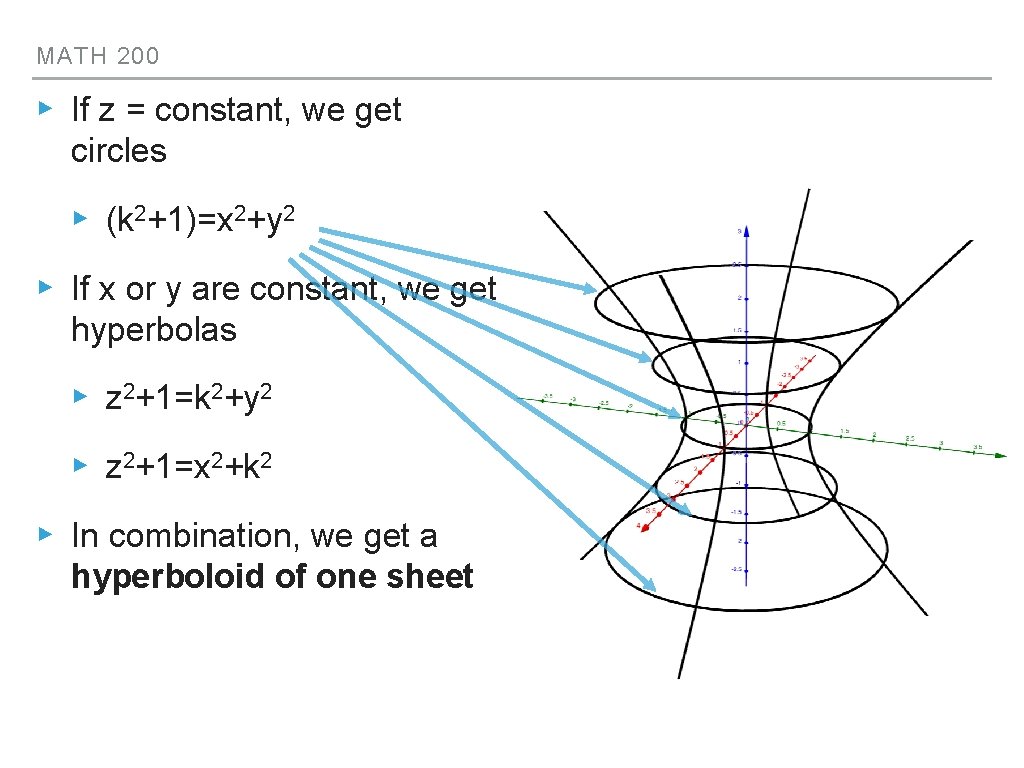
MATH 200 EXAMPLE 4 HYPERBOLOID OF ONE SHEET ▸ In the last example (z 2=x 2+y 2+1) we notice that we couldn’t get z-values between -1 and 1 ▸ How is z 2=x 2+y 2 -1 different? ▸ Writing it like this might help: z 2+1=x 2+y 2 ▸ In this case, x 2+y 2≥ 1, so inside the unit circle/cylinder is empty. ▸ The traces are still circles and hyperbolas

MATH 200 ▸ If z = constant, we get circles ▸ (k 2+1)=x 2+y 2 ▸ If x or y are constant, we get hyperbolas ▸ z 2+1=k 2+y 2 ▸ z 2+1=x 2+k 2 ▸ In combination, we get a hyperboloid of one sheet

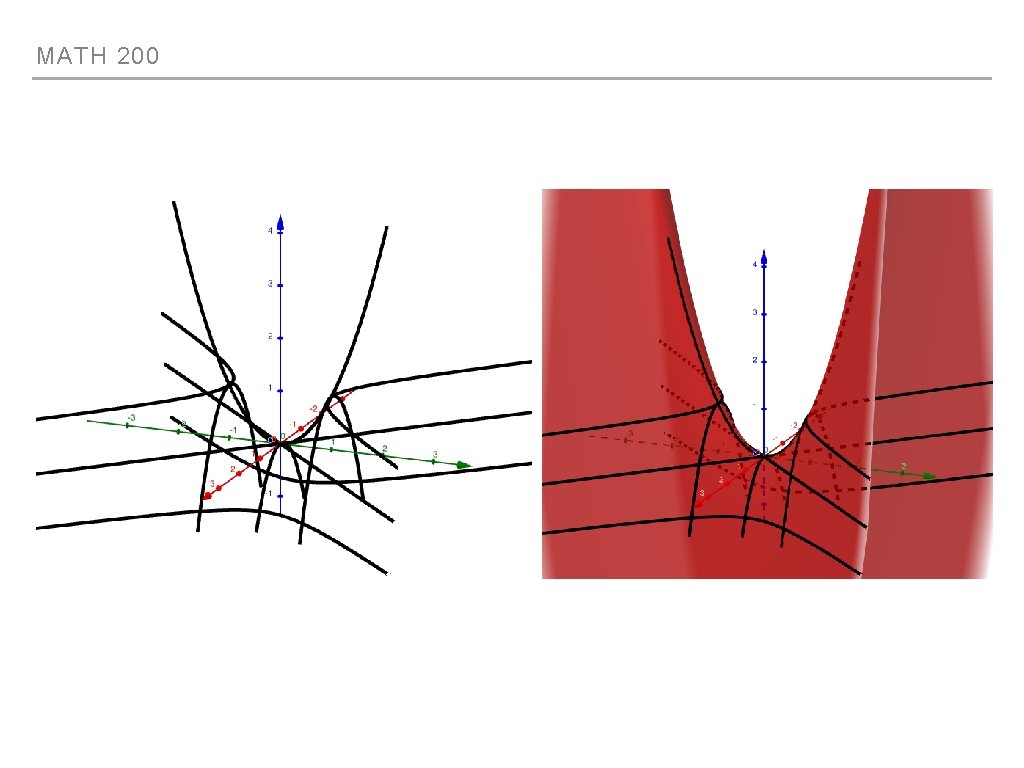
MATH 200 LASTLY…THE HYPERBOLIC PARABOLOID - AKA THE SADDLE ▸ z = y 2 - x 2 ▸ Hyperbolas for z = constant (except zero) ▸ z = 0: |x| = |y| ▸ z = 1: y 2 = x 2+1 ▸ z = -1: x 2 = y 2+1 ▸ Parabolas in opposite directions for x=const. and y=const. ▸ x=0: z = y 2 ▸ y=0: z = -x 2

MATH 200