Linear and Projectile Motion Chapters 2 3 Dr
















































































- Slides: 91

Linear and Projectile Motion (Chapters 2 -3) Dr. Walker

Relative Motion • Picture yourself riding a bike alongside another person • If both of you are riding at the same speed, does your position change relative to each other? http: //keyassets. timeincuk. net/inspirewp/live/wp-content/uploads/sites/2/2017/01/St. Neots. CC 124 -630 x 420. jpg

Relative Motion • Refers to the motion of one object versus that of another • Another example – A car pulls away from your car on the interstate. You are moving, but the car in front of you is moving at a faster speed.

It’s All Relative • Although you may be at rest relative to Earth’s surface, you’re moving about 100, 000 km/h relative to the sun.

Need For Speed • Speed = distance/time • Any combination of distance and time will work

Different Types of Speed • Instantaneous Speed – The speed you are going at any given instant – When driving, you do not always go the same speed • Slowing down in a school zone for example • Average Speed – The total distance divided by the total time

Calculating Speed • Usain Bolt holds the world record for the 100 meter dash with a time of 9. 58 s. What is his speed?

Calculating Speed • Usain Bolt holds the world record for the 100 meter dash with a time of 9. 58 s. What is his speed? • 100 m / 9. 58 s = 10. 4 m/s

Calculating Speed • In training for a race, you aim to run 4. 4 m/s (about 10 mph). If you run this pace for 30 minutes, how far did you travel in meters?

Calculating Speed • In training for a race, you aim to run 4. 4 m/s (about 10 mph). If you run this pace for 30 minutes, how far did you travel in meters? • 30 minutes x 60 sec/1 min x 4. 4 m/s = 7920 m (about 5 miles)

Calculating Speed • If a cheetah can maintain a constant speed of 25 m/s, it will cover 25 meters every second. At this rate, how far will it travel in 10 seconds? In 1 minute?

Calculating Speed • If a cheetah can maintain a constant speed of 25 m/s, it will cover 25 meters every second. At this rate, how far will it travel in 10 seconds? In 1 minute? • In 10 s the cheetah will cover 250 m, and in 1 min (or 60 s) it will cover 1500 m (almost a mile!)


Velocity • Velocity is speed in a given direction – Stating a car travels at 70 mph refers only to speed • Speed is a scalar quantity – Stating a car travels east at 70 mph refers to its velocity since a direction is given • Velocity is a vector quantity • Velocity is motion in a straight line https: //boing. net/filesroot/141_velociraptor. jpg

Changing Velocity • Since velocity must have a direction, a change in speed OR direction indicates a change in velocity • These race cars have a constantly changing velocity, since they are always changing direction https: //www. gannett-cdn. com/-mm-/d 33 c 5184 df 7 eba 7194819 e 6498 d 040 da 8343774 d/c=0 -0 -39702985&r=x 404&c=534 x 401/local/-/media/2016/10/22/USATODAY/636127442487283566 talladega-start. jpg

Food For Thought • The speedometer of a car moving northward reads 60 km/h. It passes another car that travels southward at 60 km/h. Do both cars have the same speed? Do they have the same velocity?

Speed vs. Velocity The speedometer of a car moving northward reads 60 km/h. It passes another car that travels southward at 60 km/h. Do both cars have the same speed? Do they have the same velocity? Answer: Both cars have the same speed, but they have opposite velocities because they are moving in opposite directions.

Graphing Velocity • Velocity is the change in displacement divided by the change in time. – A straight-line, position-time graph indicates constant velocity. – The slope of a displacement-time graph is the velocity.

Acceleration • Acceleration is the rate at which the velocity is changing – If your velocity is constant, then your acceleration = 0!! – Acceleration is directional (like velocity), so it is a vector quantity a = Dv/Dt

Example • A Lamborghini Huracán can travel from 0 km/h to 96 km/h (roughly 0 – 60 mph) in 2. 5 s. • What is the acceleration of this vehicle?

Example • A Lamborghini Huracán can travel from 0 km/h to 96 km/h (roughly 0 – 60 mph) in 2. 5 s. • What is the top acceleration of this vehicle? • (96 km/h – 0 km/h) / 2. 5 s = 38. 4 km/h. s • Acceleration units are velocity (km/h) per time (s). Most typically, it will be m/s. s or m/s 2

Example • A car can decelerate at roughly 7 m/s 2 on a dry road. Give the time it takes a car to go from 22 m/s (roughly 55 mph) to a standstill with this rate of deceleration.

Example • A car can decelerate at roughly 7 m/s 2 on a dry road. Give the time it takes a car to go from 22 m/s (roughly 55 mph) to a standstill with this rate of deceleration. • We have to rearrange the equation to time = (change of velocity)/acceleration • (-22 m/s) / (-7 m/s 2 ) = 3. 14 s – Why are those numbers negative? • Deceleration is negative acceleration – you’re slowing down!

Example • A car is travelling at a rate of 20 m/s, then accelerates at a rate of 2 m/s 2 for 5 seconds. What is the new velocity of the car?

Example • A car is travelling at a rate of 20 m/s, then accelerates at a rate of 2 m/s 2 for 5 seconds. What is the new velocity of the car? • We can calculate the change in velocity from a = Dv/Dt. Dv = (2 m/s 2)(5 s) = 10 m/s Now we have to add this change in speed to the initial speed. 10 m/s + 20 m/s = 30 m/s This is represented by the equation Vf = Vi + at

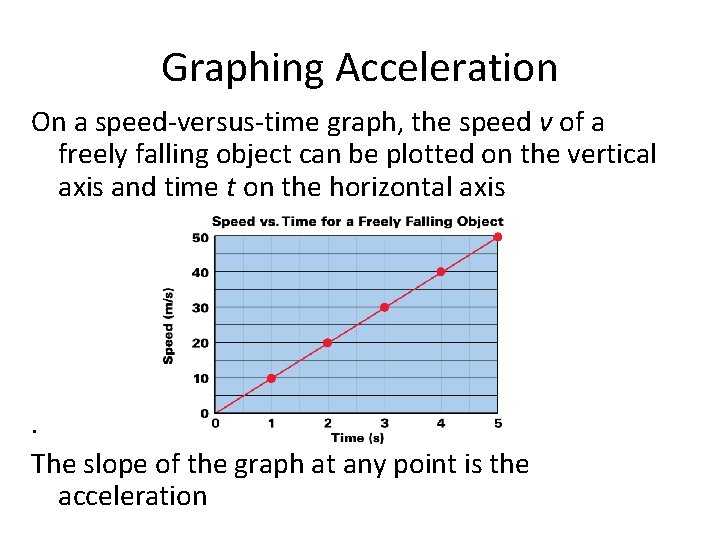
Graphing Acceleration On a speed-versus-time graph, the speed v of a freely falling object can be plotted on the vertical axis and time t on the horizontal axis . The slope of the graph at any point is the acceleration

Free Falling Imagine there is no air resistance and that gravity is the only thing affecting a falling object. – An object moving under the influence of the gravitational force only is said to be in free fall. – The elapsed time is the time that has elapsed, or passed, since the beginning of any motion, in this case the fall.

Free Fall • During each second of free fall, the an object’s speed increases by 9. 8 meters per second. • This increase is the acceleration. • We are assuming there is no air resistance. Air resistance lowers this number, especially for objects with a large surface area relative to mass like a parachute or a feather • The letter g is used to represent this quantity. – If you see an “a” it represents the same thing

Speed of Free Fall • Instantaneous speed in free fall V = gt V = velocity, g = acceleration from gravity t = time

Example • An object is in free fall for 3. 5 s. What is it’s velocity at this time?

Example • An object is in free fall for 3. 5 s. What is it’s velocity at this time? • V = gt • V = 9. 8 m/s 2 x 3. 5 s • V = 34. 3 m/s

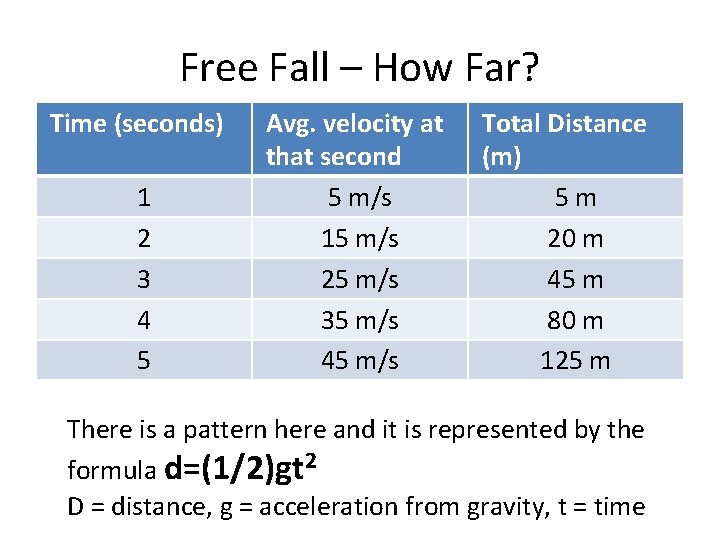
Free Fall – How Far? How far does an object in free fall travel? – In the first second, the object’s speed increases from 0 m/s to 10 m/s. • Average speed is 5 m/s • Travels 5 m (in 1 second) – In the second, the object’s speed increases from 10 m/s to 20 m/s • Average speed is 15 m/s, travels 15 meters – In the third second, the object’s speed increases from 20 m/s to 30 m/s. • Average speed is 25 m/s, travels 25 meters • Total distance after 3 seconds is 5 + 15 + 25 = 45 meters

Free Fall – How Far? Time (seconds) 1 2 3 4 5 Avg. velocity at that second 5 m/s 15 m/s 25 m/s 35 m/s 45 m/s Total Distance (m) 5 m 20 m 45 m 80 m 125 m There is a pattern here and it is represented by the formula d=(1/2)gt 2 D = distance, g = acceleration from gravity, t = time

Free Fall Example • Luke drops a pile of roof shingles from the top of a roof located 8. 52 meters above the ground. Determine the time required for the shingles to reach the ground.

Free Fall Example • Luke drops a pile of roof shingles from the top of a roof located 8. 52 meters above the ground. Determine the time required for the shingles to reach the ground. • Notice we’re solving for time, so we have to rearrange the equation. We’re not looking for distance very often. • D = 1/2 gt 2 8. 52 = ½(9. 8)t 2 8. 52 = 4. 9 x t 2 1. 74 = t 2 1. 32 = t

Free Fall Example • A basketball player has a vertical leap of 1. 0 m (39 inches). Calculate his “hang time”.

Free Fall Example • A basketball player has a vertical leap of 1. 0 m (39 inches). Calculate his “hang time”. • Again, we’re solving for time rather than distance • D = 1/2 gt 2 1. 0 m = ½(9. 8)t 2 0. 20 = t 2 0. 45 = t The trick here is that this is the time it takes for the player to go up 1. 0 m. It will take just as long for him to come down, so this number is multiplied by 2!! 2 x 0. 45 s = 0. 90 s

More Free Fall • Find the speed required to throw a ball straight up and have it return 5 s later. • (Hint: this is similar to the hang time example)

More Free Fall • Find the speed required to throw a ball straight up and have it return 5 s later. • The ball will travel up for ½ the time and travel down for ½ the time, so our time is 2. 5 s, not 5 s! • V = gt V = (9. 8 m/s 2)(2. 5 s) = 24. 5 m/s

More Free Fall • How far up must the ball be thrown straight up and have it return 5 s later?

More Free Fall • How far up must the ball be thrown straight up and have it return 5 s later? • D = ½ gt 2 D = ½ (9. 8 m/s 2)(2. 5 s)2 D = (4. 9 m/s 2)(6. 25 s 2) D = 30. 6 m Remember, the ball is only travelling up for ½ the time!

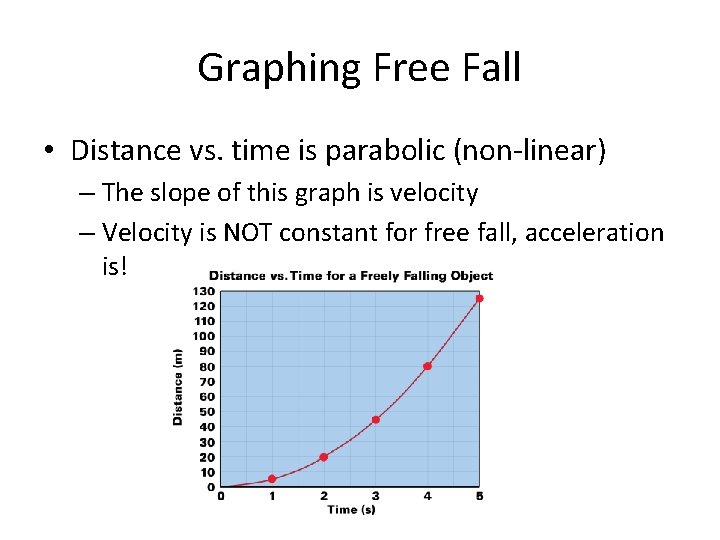
Graphing Free Fall • Distance vs. time is parabolic (non-linear) – The slope of this graph is velocity – Velocity is NOT constant for free fall, acceleration is!

Kinematic Equations • These equations describe and represent the motion of objects – Can be used for linear or projectile motion – Include equations that have been covered – Can measure distance or velocity, acceleration must be constant • Solve with “plug and chug” technique

Kinematic Equations 1 2 3 4 • Vf = Final velocity Vi = Initial Velocity • A = Acceleration T = time (in seconds) • Notice that equation 1 is similar to v = gt – We’re not starting from rest here • Notice equation 4 are similar to d = 1/2 gt 2 – We’re not starting at rest in equation 4 http: //study. com/cimages/multimages/16/four_kinematic_equations_fixed. png

Linear Kinematics – Example 1 • Ima Hurryin is approaching a stoplight moving with a velocity of +30. 0 m/s. The light turns yellow, and Ima applies the brakes and skids to a stop. If Ima's acceleration is -8. 00 m/s 2, then determine the displacement of the car during the skidding process.

Linear Kinematics – Example 1 • Ima Hurryin is approaching a stoplight moving with a velocity of +30. 0 m/s. The light turns yellow, and Ima applies the brakes and skids to a stop. If Ima's acceleration is -8. 00 m/s 2, then determine the displacement of the car during the skidding process. • What are we trying to find? • What equation should we use?

Linear Kinematics – Example 1 • Ima Hurryin is approaching a stoplight moving with a velocity of +30. 0 m/s. The light turns yellow, and Ima applies the brakes and skids to a stop. If Ima's acceleration is -8. 00 m/s 2, then determine the displacement of the car during the skidding process. • What are we trying to find? Total distance • What equation should we use? vf 2 = vi 2 + 2 • a • d

Linear Kinematics – Example 1 • Ima Hurryin is approaching a stoplight moving with a velocity of +30. 0 m/s. The light turns yellow, and Ima applies the brakes and skids to a stop. If Ima's acceleration is -8. 00 m/s 2, then determine the displacement of the car during the skidding process. • vf 2 = vi 2 + 2 • a • d • 0 = (+30. 0 m/s)2 + 2 • (-8. 00 m/s 2) • d = 56. 3 m

Linear Kinematics – Example 2 • Ben Rushin is waiting at a stoplight. When it finally turns green, Ben accelerated from rest at a rate of a 6. 00 m/s 2 for a time of 4. 10 seconds. Determine the displacement of Ben's car during this time period. • What do you have? • What are you trying to find? • What equation do you need?

Linear Kinematics – Example 2 • Ben Rushin is waiting at a stoplight. When it finally turns green, Ben accelerated from rest at a rate of a 6. 00 m/s 2 for a time of 4. 10 seconds. Determine the displacement of Ben's car during this time period. • What do you have? Acceleration, time • What are you trying to find? Total displacement • What equation do you need? d = vi • t + ½ • a • t 2

Linear Kinematics – Example 2 • Ben Rushin is waiting at a stoplight. When it finally turns green, Ben accelerated from rest at a rate of a 6. 00 m/s 2 for a time of 4. 10 seconds. Determine the displacement of Ben's car during this time period. • d = vi • t + ½ • a • t 2 • Notice the first term goes away and looks like d = 1/2 gt 2 • d = 0 + ½ • 6. 00 m/s 2 • 4. 10 s = 50. 4 m

Review – Vectors vs. Scalars • Scalar quantity – Has a magnitude only – Can be manipulated like normal numbers • Vector quantity – Has magnitude AND direction – Direction has to be accounted for when manipulated – Velocity and Acceleration are vector quantities – We didn’t worry about this last chapter – we only dealt with straight line paths

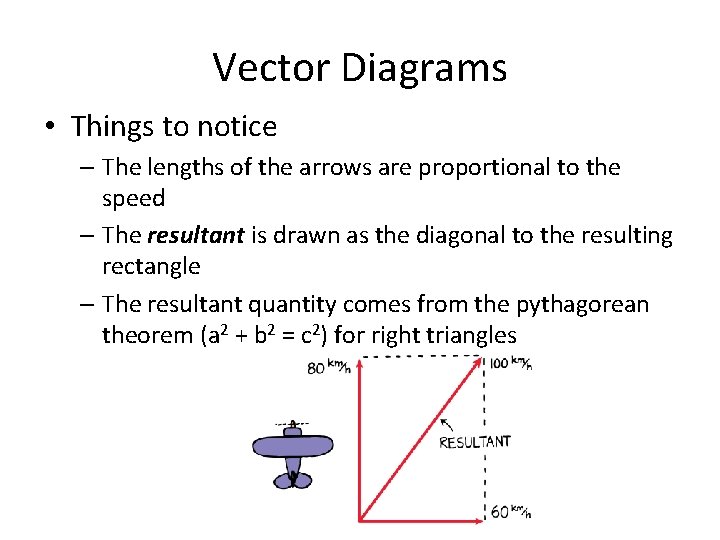
Vector Diagrams • Vector quantities are often represented by scaled vector diagrams. They depict a vector by use of an arrow drawn to scale in a specific direction

Vector Diagrams • Vector diagrams should have: – a scale is clearly listed – a vector arrow (with arrowhead) is drawn in a specified direction. The vector arrow has a head and a tail. – the magnitude and direction of the vector is clearly labeled. In this case, the diagram shows the magnitude is 20 m and the direction is East.

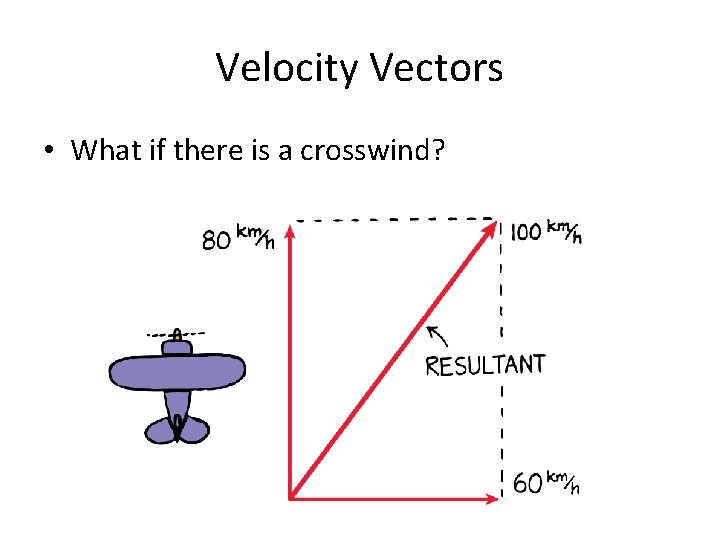
Velocity Vectors The airplane’s velocity relative to the ground depends on the airplane’s velocity relative to the air and on the wind’s velocity.

Velocity Vectors • What if there is a crosswind?

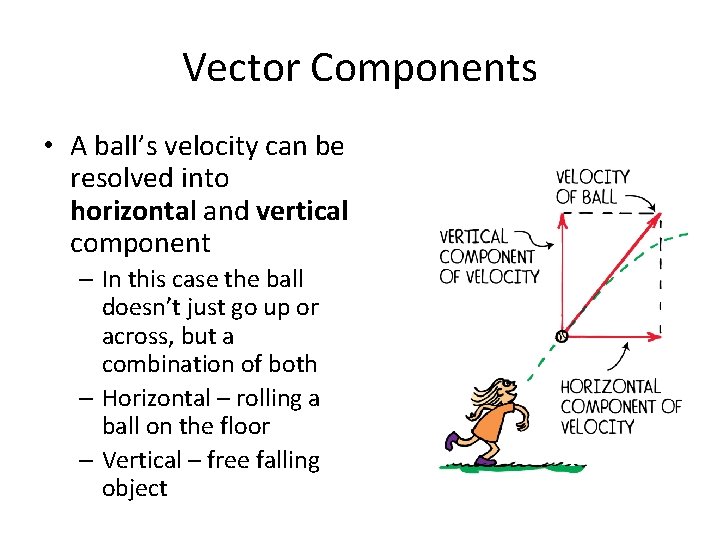
Vector Components • A ball’s velocity can be resolved into horizontal and vertical component – In this case the ball doesn’t just go up or across, but a combination of both – Horizontal – rolling a ball on the floor – Vertical – free falling object

Velocity Vectors • The plane’s speed relative to the ground can be found by adding the two vectors. • The result of adding these two vectors, called the resultant, is the diagonal of the rectangle described by the two vectors.

Vector Diagrams • Things to notice – The lengths of the arrows are proportional to the speed – The resultant is drawn as the diagonal to the resulting rectangle – The resultant quantity comes from the pythagorean theorem (a 2 + b 2 = c 2) for right triangles

What’s Your Angle? • The direction of the resulting velocity can be determined using a trigonometric function (yes, trig!) • Since the plane velocity and the wind velocity form a right triangle when added together in head-to-tail fashion, the angle between the resultant vector and the southward vector can be determined using the sine, cosine, or tangent functions. • In this case, the tangent is used. http: //www. physicsclassroom. com/class/vectors/Lesson-1/Relative-Velocity-and-Riverboat. Problems

On The River • A motorboat traveling 4 m/s, East encounters a current traveling 7. 0 m/s, North. – What is the resultant velocity of the motorboat? – At what angle does it travel up the river? – If the width of the river is 80 meters wide, then how much time does it take the boat to travel shore to shore? – What distance downstream does the boat reach the opposite shore?

On The River • A motorboat traveling 4 m/s, East encounters a current traveling 7. 0 m/s, North. – What is the resultant velocity of the motorboat? – Use the Pythagorean theorem to find the length of the resultant • (4. 0)2 + (7. 0)2 = C 2 • C = 8. 06 m/s

On The River • A motorboat traveling 4 m/s, East encounters a current traveling 7. 0 m/s, North. – At what angle does it travel up the river? – q = tan(opposite/adjacent) – q = tan (7/4) – q = 60 o 7. 0 m/s q 4. 0 m/s

On The River • A motorboat traveling 4 m/s, East encounters a current traveling 7. 0 m/s, North. – If the width of the river is 80 meters wide, then how much time does it take the boat to travel shore to shore? – Time = Distance/Speed – (80 m)(4. 0 m/s) = 20 s • Why did we did 4. 0 m/s instead of the resultant? – Width of the river – we’re only using the horizontal vector, not the resultant

On The River • A motorboat traveling 4 m/s, East encounters a current traveling 7. 0 m/s, North. – What distance downstream does the boat reach the opposite shore? – Distance = Speed x Time – Distance = 7. 0 m/s x 20 s = 140 m – We used the time from the previous step and the “vertical” vector to determine distance downstream.

Vector Jokes

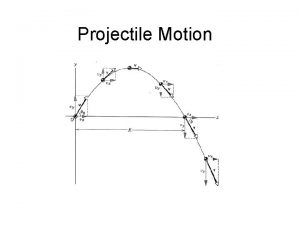
Projectile Motion • Projectile – Any object that moves through the air or space, acted on only by gravity (and air resistance if present) – Examples • A bullet being fired from a gun • A ball being thrown • A car (or anything else) rolling off of a cliff

Projectile Motion • Linear motion involves motion in a straight path (linear…. line) • Projectile motion involves motion on a curved path – A curve has multiple directions • Horizontal • Vertical

Components of Projectile Motion • Horizontal – Constant velocity, no force of gravity • Vertical – Downward acceleration due to gravity • Increasing velocity • Greater distance covered each second an object falls • These components are independent of one another

Projectile Motion Demonstrated • A strobe-light photo of two balls released simultaneously–one ball drops freely while the other one is projected horizontally. Notice: 1) The horizontal motion is constant – there is no acceleration 2) Both balls cover the same vertical distance per unit time 3) This path is a parabola

A Thought Experiment • A cannonball is fired at the same time another is dropped from the same height. Which one hits the ground first?

A Thought Experiment • A cannonball is fired at the same time another is dropped from the same height. Which one hits the ground first? • Answer: Trick question! Gravity acts on both equally. The horizontal motion of the fired cannonball has no effect on vertical motion, just like the strobe light example

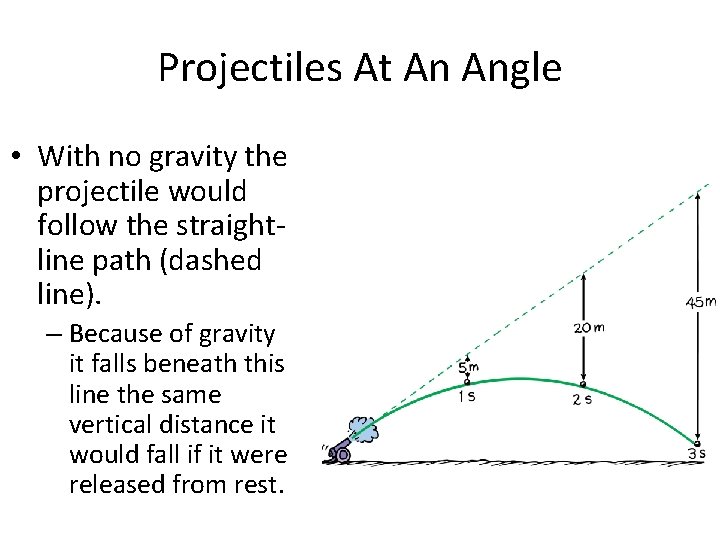
Projectiles At An Angle • With no gravity the projectile would follow the straightline path (dashed line). – Because of gravity it falls beneath this line the same vertical distance it would fall if it were released from rest.

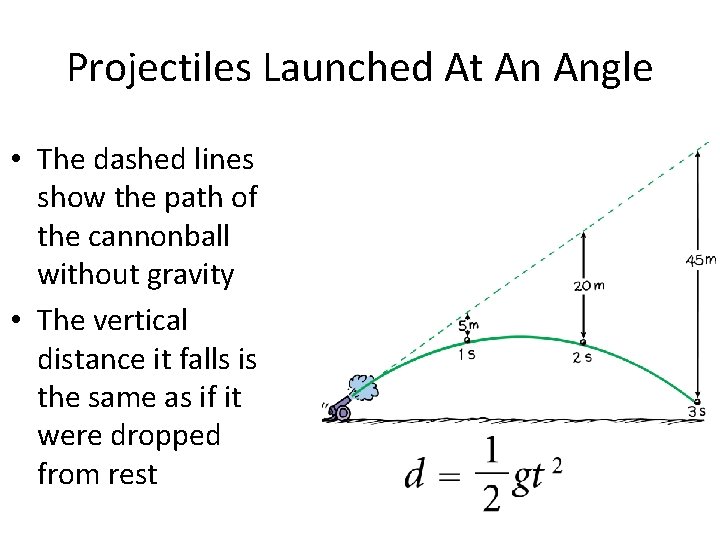
Projectiles Launched At An Angle • The dashed lines show the path of the cannonball without gravity • The vertical distance it falls is the same as if it were dropped from rest

Projectiles Launched At An Angle • From a vector standpoint – Horizontal component is always the same – The vertical component constantly changes – The velocity is the resultant of the two vectors at any point in time • At the apex (top of the curve), there is no vertical component – As a result, the velocity is lowest at the top of the curve

Projectiles Launched At An Angle • The velocity of a projectile is shown at various points along its path. Notice that the vertical component changes while the horizontal component does not. Air resistance is neglected. • Note the velocity is constantly changing, because it is a vector quantity

Projectiles Launched At An Angle • Range – The distance that a projectile travels • For example, the range of ammunition – The angle at which the projectile is launched affects the distance that it travels – Notice the difference between the horizontal velocity bectors below

Projectile Launched At An Angle • Projectiles that are launched at different angles not only have different ranges, but reach different heights above the ground – This is shown by the differences in the vertical vectors

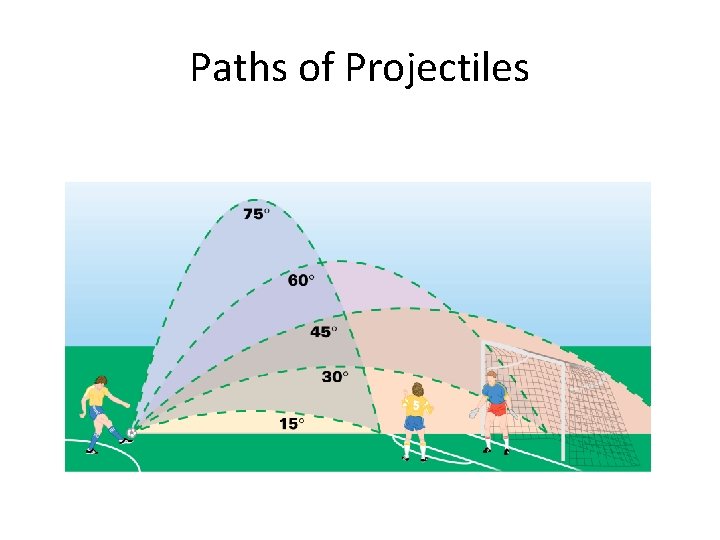
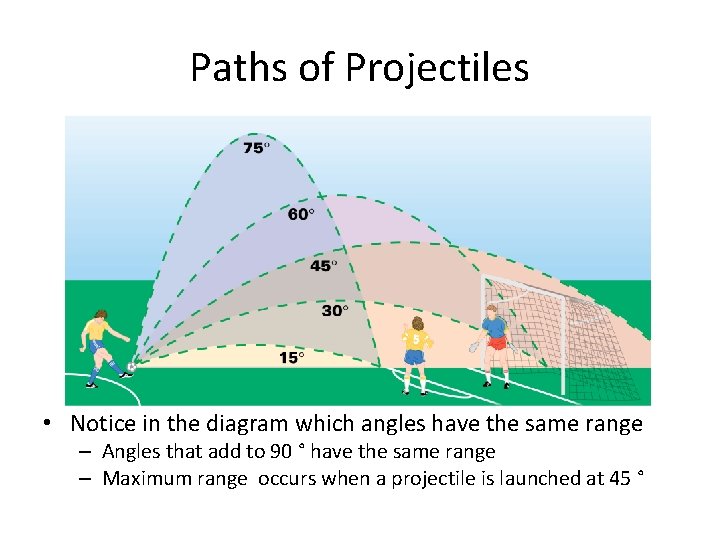
Paths of Projectiles

Paths of Projectiles • Notice in the diagram which angles have the same range – Angles that add to 90 ° have the same range – Maximum range occurs when a projectile is launched at 45 °

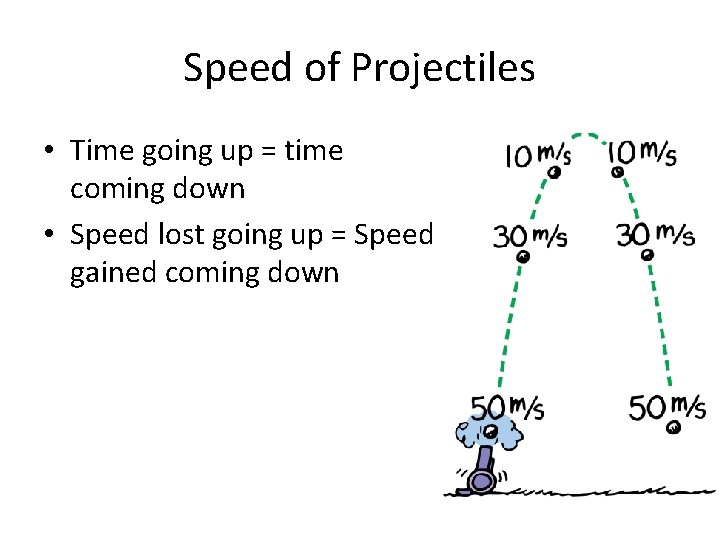
Speed of Projectiles • Without air resistance, a projectile will reach maximum height in the same time it takes to fall from that height to the ground. • The deceleration due to gravity going up is the same as the acceleration due to gravity coming down. • The projectile hits the ground with the same speed it had when it was projected upward from the ground.

Speed of Projectiles • Time going up = time coming down • Speed lost going up = Speed gained coming down

Projectile Problems • Remember, there is a horizontal and vertical component to a projectile • Horizontally… – How far? D = v • t – How fast? V = d/t • Vertically…. – How far? D = (1/2) • g • t 2 – How fast? D = g • t – Here g = acceleration due to gravity. We differentiate it from “a” because it’s specific to gravity

Horizontally Launched Projectiles • A pool ball leaves a 0. 60 -meter high table with an initial horizontal velocity of 2. 4 m/s. Predict the time required for the pool ball to fall to the ground and the horizontal distance between the table's edge and the ball's landing location.

Horizontally Launched Projectiles • A pool ball leaves a 0. 60 -meter high table with an initial horizontal velocity of 2. 4 m/s. Predict the time required for the pool ball to fall to the ground and the horizontal distance between the table's edge and the ball's landing location. – What information do we have? • Horizontally, v = 2. 4 m/s, a = 0, looking for d • Vertically g = 9. 8 m/s 2, vi = 0 m/s, d = 0. 60 m, looking for t

Horizontally Launched Projectiles • A pool ball leaves a 0. 60 -meter high table with an initial horizontal velocity of 2. 4 m/s. Predict the time required for the pool ball to fall to the ground and the horizontal distance between the table's edge and the ball's landing location. – What equations do we use? – For horizontal distance: x = vix • t +0. 5 • g • t 2 – For time required to drop: y = viy • t +0. 5 • g • t 2

Horizontally Launched Projectiles • A pool ball leaves a 0. 60 -meter high table with an initial horizontal velocity of 2. 4 m/s. Predict the time required for the pool ball to fall to the ground and the horizontal distance between the table's edge and the ball's landing location. – What equations do we use? – For time required to drop: y = viy • t +0. 5 • g • t 2 • The vertical velocity isn’t mentioned – it’s zero so that part cancels out • 0. 60 m = 0. 5 x 9. 8 m/s 2 x t 2 • t = 0. 35 s

Horizontally Launched Projectiles • A pool ball leaves a 0. 60 -meter high table with an initial horizontal velocity of 2. 4 m/s. Predict the time required for the pool ball to fall to the ground and the horizontal distance between the table's edge and the ball's landing location. – What equations do we use? – For horizontal distance: x = vix • t +0. 5 • g • t 2 • Since there no horizontal acceleration, the second term = 0. • X = (2. 4 m/s)(0. 35 s) =0. 84 m

Another Example • A soccer ball is kicked horizontally off a 22. 0 -meter high hill and lands a distance of 35. 0 meters from the edge of the hill. Determine the initial horizontal velocity of the soccer ball.

Another Example • A soccer ball is kicked horizontally off a 22. 0 -meter high hill and lands a distance of 35. 0 meters from the edge of the hill. Determine the initial horizontal velocity of the soccer ball. – – Vertical first – need to determine time y = viy • t +0. 5 • g • t 2 22. 0 m = 0. 5 (9. 8 m/s 2) (t 2) t = 2. 1 s

Another Example • A soccer ball is kicked horizontally off a 22. 0 -meter high hill and lands a distance of 35. 0 meters from the edge of the hill. Determine the initial horizontal velocity of the soccer ball. – – Determine velocity with horizontal x = vix • t + 0. 5 • g • t 2 35. 0 m = v (2. 1 s) v = 16. 7 m/s
 Velocity eq
Velocity eq Conceptual physics chapter 5 projectile motion answers
Conceptual physics chapter 5 projectile motion answers Chapter 10 projectile and satellite motion
Chapter 10 projectile and satellite motion Projectile motion ppt template
Projectile motion ppt template Similarity between freefall and projectile motion
Similarity between freefall and projectile motion Chapter 10 projectile and satellite motion tossed ball
Chapter 10 projectile and satellite motion tossed ball What is the only force acting on a projectile
What is the only force acting on a projectile Symmetrical projectile motion
Symmetrical projectile motion Motion map examples
Motion map examples A fourteen line lyric poem
A fourteen line lyric poem An object in projectile motion will follow which path?
An object in projectile motion will follow which path? The only force acting on a projectile is
The only force acting on a projectile is It is an object upon which the only force acting is gravity
It is an object upon which the only force acting is gravity What is a projectile
What is a projectile The physics classroom projectile motion
The physics classroom projectile motion Projectile motion examples
Projectile motion examples Projectile motion simulator
Projectile motion simulator Which describes an object in projectile motion?
Which describes an object in projectile motion? Motion of a projectile
Motion of a projectile Tennis ball in motion
Tennis ball in motion Examples of projectile motion in volleyball
Examples of projectile motion in volleyball Vyf in projectile motion
Vyf in projectile motion Non symmetric projectile motion
Non symmetric projectile motion A projectile has a single force that acts upon it
A projectile has a single force that acts upon it V
V Symmetrical projectile motion
Symmetrical projectile motion Is projectile
Is projectile Projectile motion objectives
Projectile motion objectives Projectile motion equations
Projectile motion equations Physics c
Physics c Projectile kinematic equations
Projectile kinematic equations Projectile motion equations
Projectile motion equations Objects that exhibit projectile motion follow a path.
Objects that exhibit projectile motion follow a path. Vertical motion formula
Vertical motion formula What is the shape of the trajectory of a projectile? *
What is the shape of the trajectory of a projectile? * Law of projectile motion
Law of projectile motion What force besides gravity acts on a projectile
What force besides gravity acts on a projectile A force that opposes motion of a projectile
A force that opposes motion of a projectile A factor that affects the flight of a projectile is
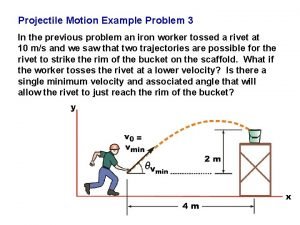
A factor that affects the flight of a projectile is Projectile motion example problems
Projectile motion example problems Horizontal velocity
Horizontal velocity Chapter 5 projectile motion
Chapter 5 projectile motion Non projectile motion
Non projectile motion Projectile motion equations
Projectile motion equations Quadratic formula word problems
Quadratic formula word problems Six sigma catapult project
Six sigma catapult project Vertical
Vertical Javelin throw way in achieving projectile motion
Javelin throw way in achieving projectile motion Parametric projectile motion
Parametric projectile motion Regents physics projectile motion questions
Regents physics projectile motion questions Projectile motion examples
Projectile motion examples Range of projectile formula
Range of projectile formula Projectile motion formulas
Projectile motion formulas Which describes an object in projectile motion?
Which describes an object in projectile motion? Projectile motion animation
Projectile motion animation Final horizontal velocity
Final horizontal velocity Motion
Motion Projectile motion
Projectile motion Air resistance formula
Air resistance formula Projectile motion review
Projectile motion review Projectile motion rules
Projectile motion rules X=vxt
X=vxt A long jumper leaves the ground at an angle of 45
A long jumper leaves the ground at an angle of 45 Honors physics projectile motion test
Honors physics projectile motion test The motion of a projectile is often studied in terms of
The motion of a projectile is often studied in terms of Projectile motion
Projectile motion Vo^2 sin 2 theta/g
Vo^2 sin 2 theta/g Projectile motion
Projectile motion Refers to the path raised by a projectile during its motion
Refers to the path raised by a projectile during its motion Projectile motion
Projectile motion Projectile motion ball
Projectile motion ball Movimento vertical
Movimento vertical Projectile motion in gymnastics
Projectile motion in gymnastics Wesbury college
Wesbury college Percent error formula
Percent error formula Parts of projectile motion illustration
Parts of projectile motion illustration Projectile motion examples
Projectile motion examples What is c
What is c The only force acting on a projectile
The only force acting on a projectile Mythbusters projectile motion
Mythbusters projectile motion Projectile motion equations
Projectile motion equations Holonomic drive
Holonomic drive Solving kinematic equations
Solving kinematic equations Meaning of projectile motion
Meaning of projectile motion Projectile motion
Projectile motion Physics javelin projectile motion
Physics javelin projectile motion Projectile motion horizontal distance
Projectile motion horizontal distance Projectile motion
Projectile motion Projectile motion
Projectile motion Projectile motion
Projectile motion Type of range of motion
Type of range of motion Analogy between translational and rotational motion
Analogy between translational and rotational motion