Outline n n n n n 4 1

Outline n n n n n 4 -1 What Is Physics? 4 -2 Position and Displacement 4 -3 Average Velocity and Instantaneous Velocity 4 -4 Average Acceleration and Instantaneous Acceleration 4 -5 Projectile Motion 4 -6 Projectile Motion Analyzed 4 -7 Uniform Circular Motion 4 -8 Relative Motion in One Dimension 4 -9 Relative Motion in Two Dimensions 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 2

4 -1 What Is Physics? n We will continue to study the motion of objects without the restriction we put in chapter 2 to move along a straight line. n Instead, we will consider motion in a plane (two dimensional motion) and motion in space (three dimensional motion). 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 3

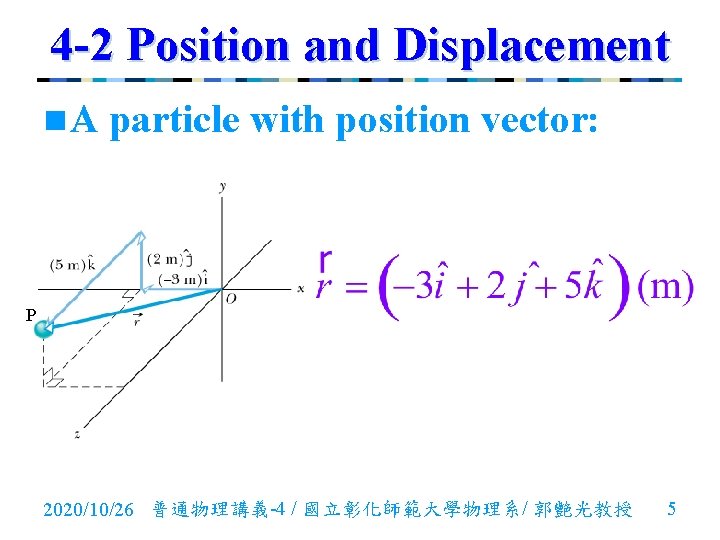
4 -2 Position and Displacement n Position Vector: It is a vector that extends from a reference point (usually the origin of a coordinate system) to the particle. n In the unit-vector notation of Section 35, can be written 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 4

4 -2 Position and Displacement n. A particle with position vector: P 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 5

4 -2 Position and Displacement n Displacement Vector: From to during a certain time interval then the particle’s displacement during that time interval is 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 6

4 -2 Position and Displacement n We can rewrite this displacement as 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 7

Example 4 -1 n The position vector for a particle initially is and then later is What is the particle’s displacement from to. 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 8

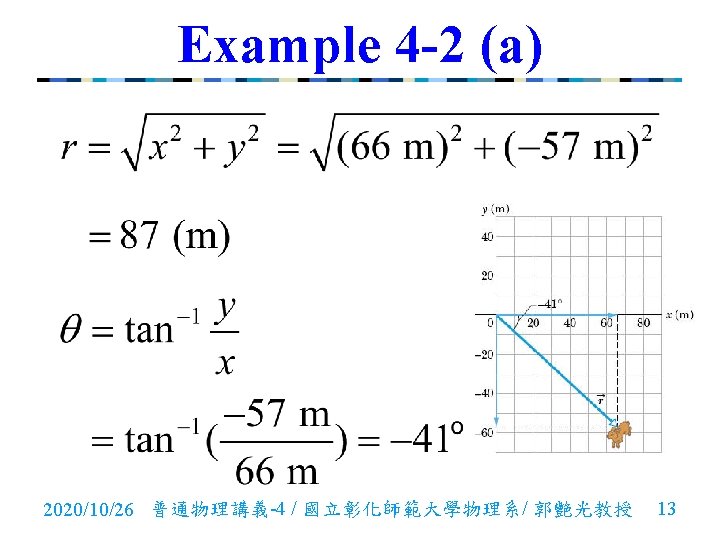
Example 4 -2 (a) n. A rabbit runs across a parking lot on which a set of coordinate axes has, strangely enough, been drawn. The coordinates of the rabbit’s position as functions of time t are given by and , with t in seconds and x and y in meters. At , what is the rabbit’s position vector in unit-vector notation and in magnitude-angle notation? 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 10

Example 4 -2 (a) n Key idea: The x and y coordinates of the rabbit’s position, are the scalar components of the rabbit’s position vector. n Solutions: We can write 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 11

Example 4 -2 (a) At , the scalar components are so 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 12

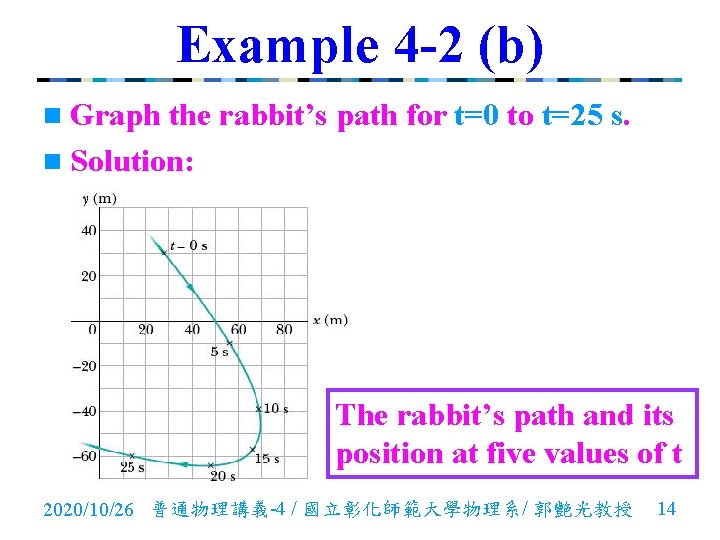
Example 4 -2 (b) n Graph the rabbit’s path for t=0 to t=25 s. n Solution: The rabbit’s path and its position at five values of t 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 14

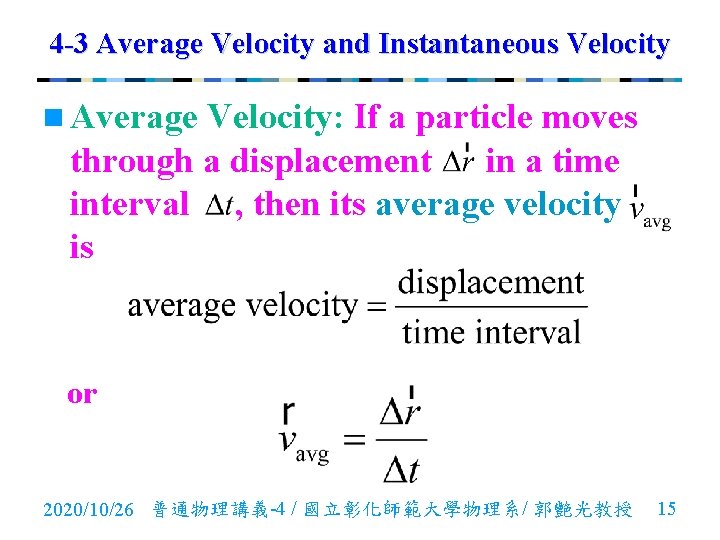
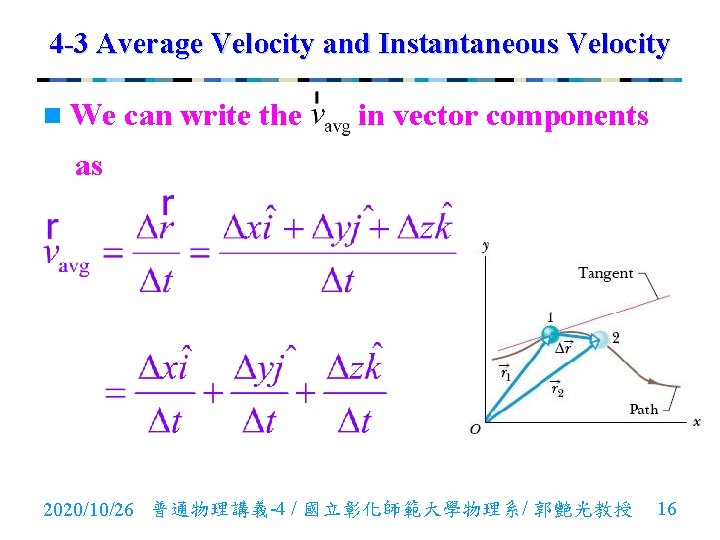
4 -3 Average Velocity and Instantaneous Velocity n Average Velocity: If a particle moves through a displacement in a time interval , then its average velocity is or 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 15

4 -3 Average Velocity and Instantaneous Velocity n We can write the in vector components as 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 16

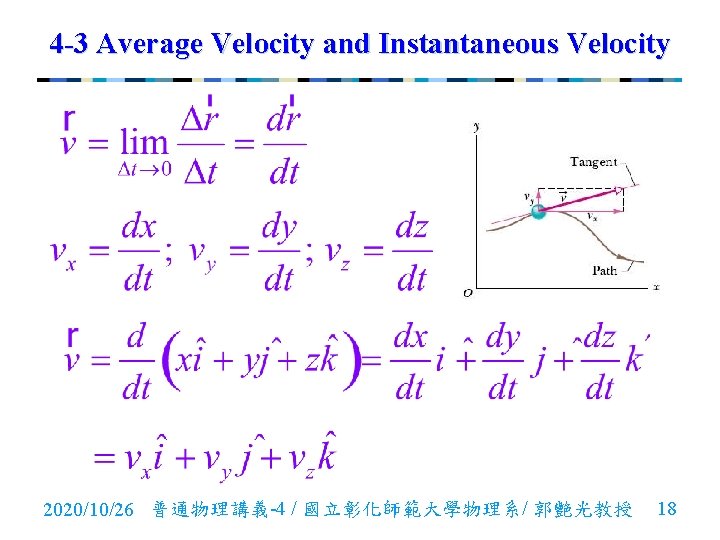
4 -3 Average Velocity and Instantaneous Velocity n Instantaneous Velocity: It is the value that approaches in the limit as we shrink the time interval to 0 about that instant. : instantaneous velocity 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 17

4 -3 Average Velocity and Instantaneous Velocity 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 18

Example 4 -3 For the rabbit in example 4 -2, find the velocity at time t = 15 s. n Solutions: n 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 19

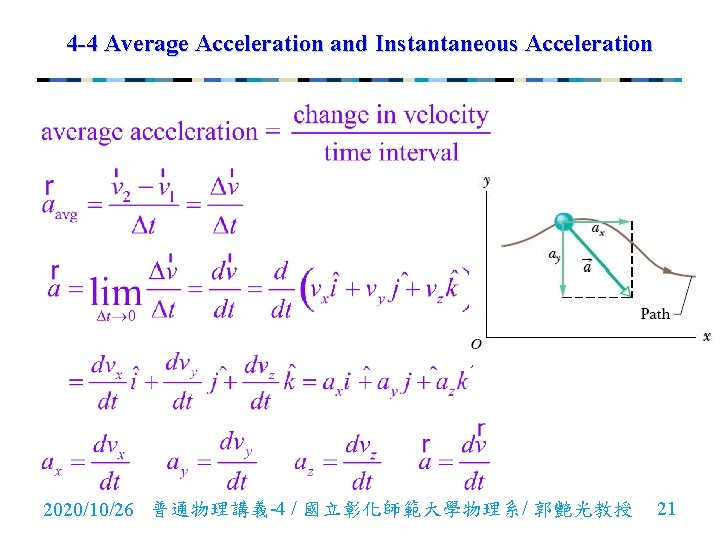
4 -4 Average Acceleration and Instantaneous Acceleration n Average acceleration: A particle’s velocity changes from to in a time interval , its average acceleration during is or 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 20

4 -4 Average Acceleration and Instantaneous Acceleration 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 21

Example 4 -4 n For the rabbit in example 4 -2 and 4 -3, find the acceleration at time t = 15 s. n Solutions: 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 22

Example 4 -5 n. A particle with velocity (in meters per second) at undergoes a constant acceleration of magnitude at an angle from the positive direction of the x axis. What is the particle’s velocity at. n Solutions: 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 23

4 -5 Projectile Motion n Projectile motion: A particle moves in a vertical plane and its acceleration is the freefall acceleration , which is downward. 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 25

4 -6 Projectile Motion Analyzed n Horizontal Motion: Because there is no acceleration in the horizontal direction, the horizontal component of the projectile’s remains unchanged from its initial value throughout the motion. 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 26

4 -6 Projectile Motion Analyzed n Vertical Motion: 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 27

4 -6 Projectile Motion Analyzed n The Equation of the Path: 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 28

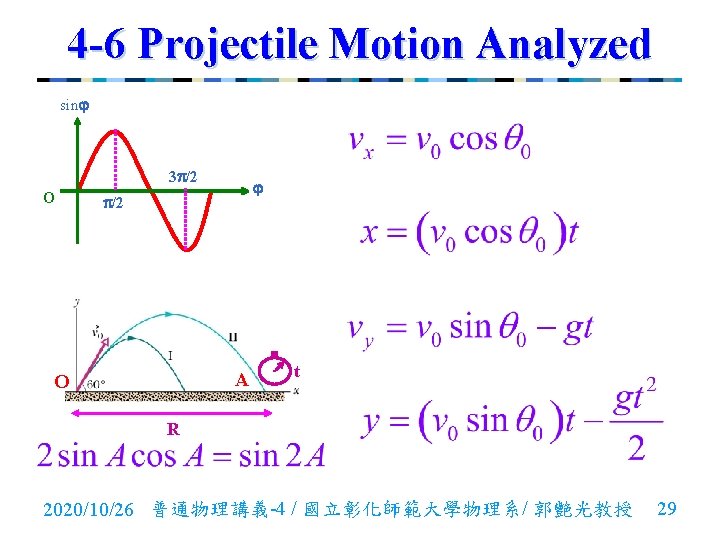
4 -6 Projectile Motion Analyzed sin 3 /2 O /2 A O t R 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 29

4 -6 Projectile Motion Analyzed n The Horizontal Range: It is the horizontal distance the projectile has traveled when if returns to its initial (launch) height. n Let in and in , obtaining and 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 30

4 -6 Projectile Motion Analyzed R has its maximum value when to or. , which corresponds 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 31

4 -6 Projectile Motion Analyzed n Maximum height H: 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 32

Example 4 -6 (a) n. A rescue plane flies at 198 km/h ( = 55. 0 m/s ) and a constant elevation of 500 m toward a point directly over a boating accident victim struggling in the water. 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 34

Example 4 -6 (a) n The pilot wants to release a rescue capsule so that it hits the water very close to the victim. What should be the angle of the pilot’s line of sight to the victim when the release is made? n Solutions: 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 35

Example 4 -6 (b) n As the capsule reaches the water, what is its velocity in unit-vector notation and in magnitude-angle notation? n Solutions: 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 37

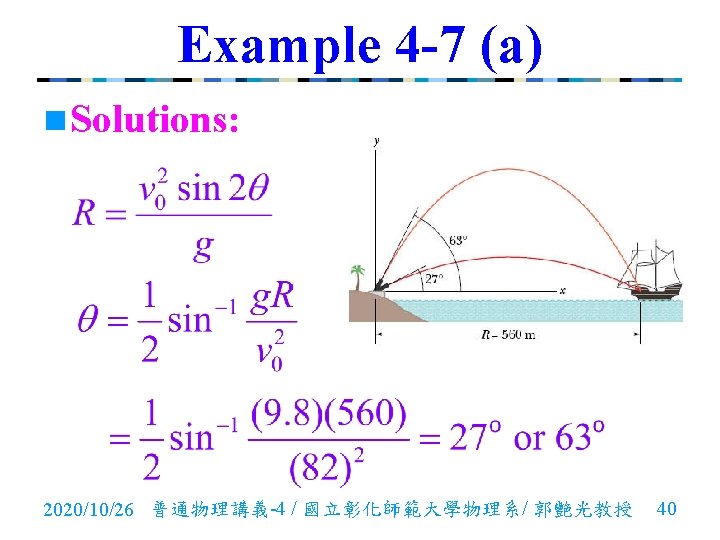
Example 4 -7 (a) n. A pirate ship 560 m from a fort defending the harbor entrance of an island. A defense cannon, located at sea level, fires balls at initial speed v 0 = 82 m/s. At what angle from the horizontal must a ball be fired to hit the ship? 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 39

Example 4 -7 (b) n How far should the pirate ship be from the cannon if it is to be beyond the maximum range of the cannonballs? n Solutions: 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 41

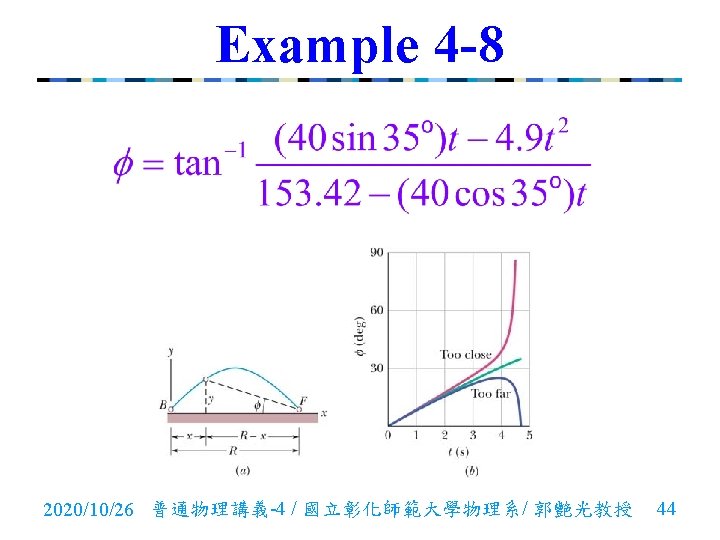
Example 4 -8 n Suppose a baseball batter B hits a high fly ball to the outfield, directly toward an outfielder F and with a launch speed of and a launch angle of. During the flight, a line from the outfielder to the ball makes an angle with the ground. Plot elevation angle versus time t, 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 42

Example 4 -8 assuming that the outfielder is already positioned to catch the ball, is 6. 0 m too close to the batter, and is 6. 0 m too far away. n Solutions: 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 43

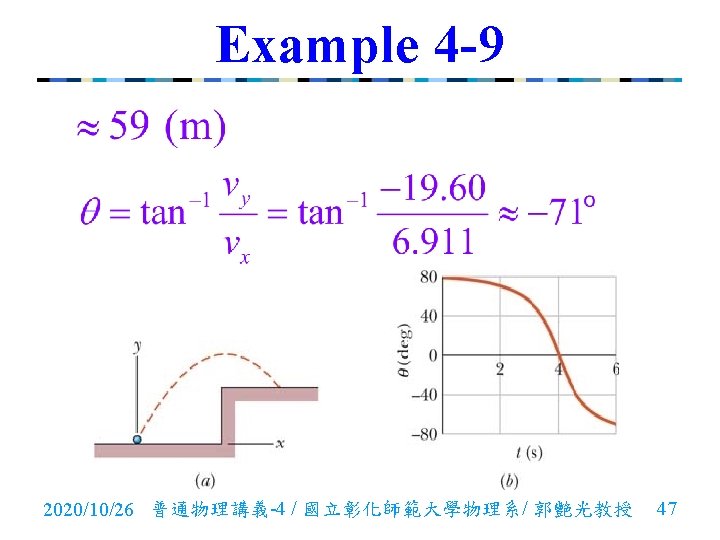
Example 4 -9 n At time = 0, golf ball is shot from ground level into the air, as indicated in Fig. (a). The angle between the ball’s direction of travel and the positive direction of the x axis is given in Fig. (b) as a function of time t. The ball lands at t = 6. 00 s. What is the magnitude of the ball’s launch velocity, at what height above the launch level does the ball land, and what is the ball’s direction of travel just as it lands? 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 45

4 -7 Uniform Circular Motion n It travels around a circle or a circular arc at constant (uniform) speed. n The speed does not vary, the particle is accelerating. n The acceleration is always directed radially inward. n The acceleration is called a centripetal acceleration. 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 48

4 -7 Uniform Circular Motion n The magnitude of this acceleration is n The particle travels the circumference of the circle ( a distance of 2 r ) in time T: Period of revolution 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 49

4 -7 Uniform Circular Motion n Prove: The scalar components of are shown in Fig. (b). With them, we can write the velocity as 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 50

4 -7 Uniform Circular Motion using the right triangle in Fig. (a), we can replace with and with to write 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 51

4 -7 Uniform Circular Motion from Fig. (b), this vector and its components are show in Fig. (c). We find 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 52

Example 4 -10 n “Top gun” pilots have long worried about taking a turn too tightly. As a pilot’s body undergoes centripetal acceleration, with the head toward the center of curvature, the blood pressure in the brain decreases, leading to loss of brain function. There are several warning signs to signal a pilot to ease up. When the centripetal acceleration is 2 g or 3 g, the pilot feels heavy. At about 4 g, the pilot’s vision switches to black 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 54

Example 4 -10 and white and narrows to “tunnel vision. ” If that acceleration is sustained or increased, vision ceases and, soon after, the pilot is unconscious — a condition known as g-LOC for “g-induced loss of consciousness. ” What is the centripetal acceleration, in g units, of a pilot whose aircraft enters a horizontal circular turn with a velocity of m/s and 24. 0 later leaves the turn with a velocity of m/s ? 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 55

Example 4 -11 n The moon orbits the earth with a period of 27. 3 d at a distance of m from the center of the earth. Find its centripetal acceleration. n Solution: 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 57

4 -8 Relative Motion in One Dimension 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 58

Example 4 -12 (a) n Suppose that Barbara’s velocity relative to Alex is a constant v. BA = 52 km/h and car P is moving in the negative direction of the x axis. If Alex measures a constant velocity v. PA = − 78 km/h for car P, what velocity v. PB will Barbara measure? 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 59

Example 4 -12 (a) n Solutions: We find thus, 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 60

Example 4 -12 (b) n If car P brakes to a stop relative to Alex (and thus relative to the ground) in time t = 10 s at constant acceleration, what is its acceleration a. PA relative to Alex? n Solutions: 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 61

Example 4 -12 (c) n What is the acceleration a. PB of car P relative to Barbara during the braking ? n Solutions: 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 62

4 -9 Relative Motion in Two Dimensions 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 63

4 -9 Relative Motion in Two Dimensions 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 64

Example 4 -13 n. A plane moves due east while the pilot points the plane somewhat south of east, toward a steady wind that blows to the northeast. The plane has velocity relative to the wind, with an airspeed (speed relative to the wind) of 215 km/h, directed at angle south of east. The wind has velocity relative to the ground, 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 65

Example 4 -13 with a speed of 65. 0 km/h, directed 20. 0° east of north. What is the magnitude of the velocity of the plane relative to the ground, and what is ? 2020/10/26 普通物理講義-4 / 國立彰化師範大學物理系/ 郭艷光教授 66