Projectile Motion Major Principles for All Circumstances Horizontal

Projectile Motion Major Principles for All Circumstances • Horizontal motion is constant velocity • Vertical motion is constant downward acceleration • a = g = -9. 8 m/s 2

Projectile Motion The Big Four + One More In x In y Tie s th • x = vxt • y = voyt + 1/2 gt 2 em • v = v + gt t Time & o • v = vge+ 2 gy t her Launch • y = 1/2(v + v )t y 2 y Angle oy 2 oy oy y

Projectile Motion Types of Projectile Problems • Type A - Half of a Parabola • Type B - Full Parabola - Symmetric • Type C - Partial or Asymmetric Parabola

Projectile Motion Type A - Half of a Parabola In the vertical direction • The object acts like a dropped object • Initial vertical velocity is zero; voy = 0

Projectile Motion Type A - Half of a Parabola WARNING: To solve for time, often you will use. . . y = voyt + 1/2 gt 2 since voy = 0 y = 1/2 gt 2 Be careful using Therefore. . . shortcut t = (2 y/g) formulas!!!!

Projectile Motion Type A - Half of a Parabola If the problem is reversed. . . Romeo throws a rock up to Juliet; hits window horizontally Because of symmetry, just solve the problem backwards, make voy = 0

Projectile Motion Type B - Full Parabola Notice the ball lands back in the truck. . . only if the truck moves with constant velocity

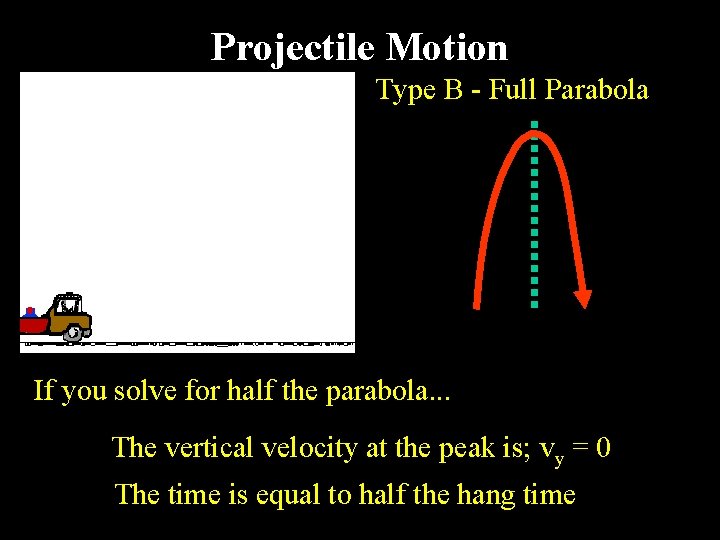
Projectile Motion Type B - Full Parabola If you solve for the full parabola. . . The vertical displacement is zero; y = 0 The time is the total hang time

Projectile Motion Type B - Full Parabola If you solve for half the parabola. . . The vertical velocity at the peak is; vy = 0 The time is equal to half the hang time

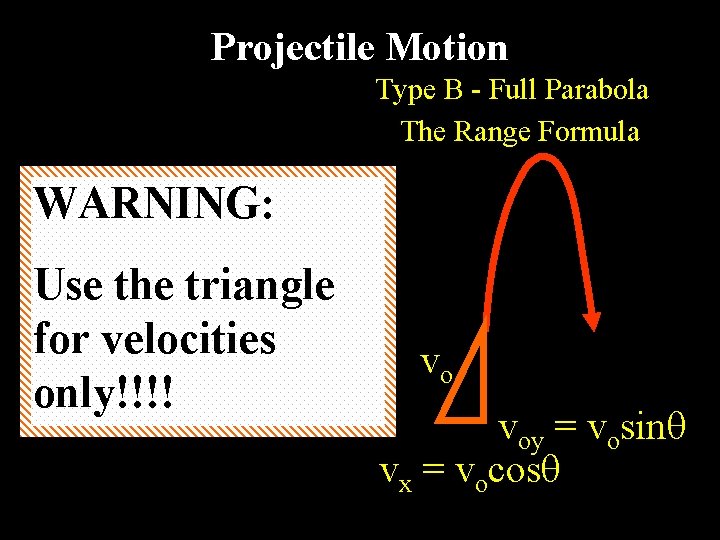
Projectile Motion Type B - Full Parabola The Range Formula WARNING: Use the triangle for velocities only!!!! vo voy = vosin vx = vocos

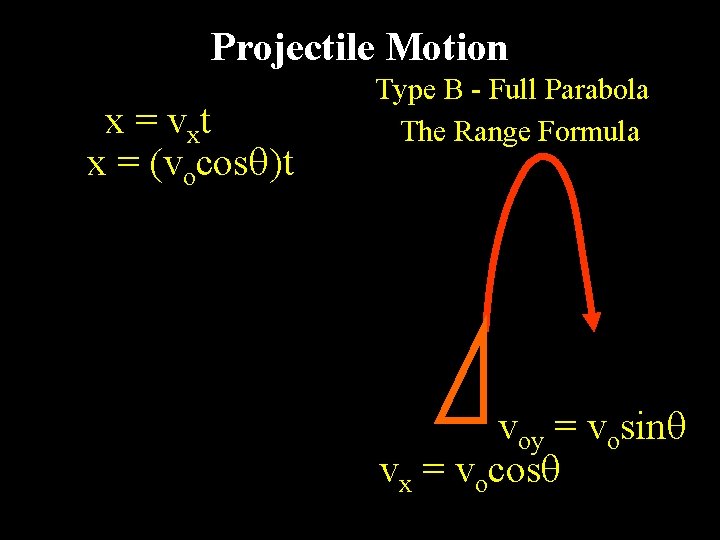
Projectile Motion x = vxt x = (vocos )t Type B - Full Parabola The Range Formula voy = vosin vx = vocos

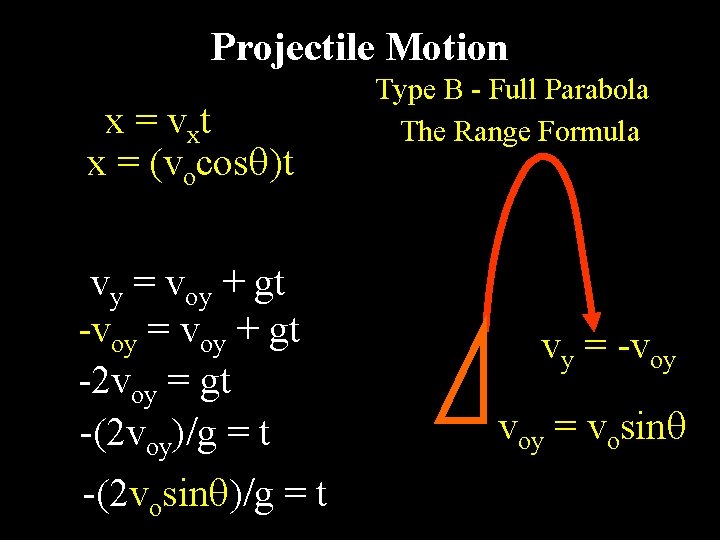
Projectile Motion x = vxt x = (vocos )t vy = voy + gt -voy = voy + gt -2 voy = gt -(2 voy)/g = t -(2 vosin )/g = t Type B - Full Parabola The Range Formula vy = -voy = vosin

Projectile Motion x = vxt x = (vocos )t Type B - Full Parabola The Range Formula x = (vocos )(-2 vosin /g) -(2 vosin )/g = t

Projectile Motion x = vxt x = (vocos )t Type B - Full Parabola The Range Formula x = (vocos )(-2 vosin /g)

Projectile Motion x = vxt x = (vocos )t Type B - Full Parabola The Range Formula x = (vocos )(-2 vosin /g) x = -vo 2(2 sin cos )/g Trig Identity: 2 sin cos = sin 2 x= 2 -vo sin 2 /g

Projectile Motion x = vxt x = (vocos )t Type B - Full Parabola The Range Formula x = (vocos )(-2 vosin /g) x = -vo 2(2 sin cos )/g x = -vo 2 sin 2 /g

Projectile Motion x = vxt x = (vocos )t Type B - Full Parabola The Range Formula x = (vocos )(-2 vosin /g) WARNING: x = -vo 2(2 sin cos )/g Be careful using x = -vo 2 sin 2 /g shortcut formulas!!!!

Projectile Motion Type B - Full Parabola • Optimum Angle of 45 Maximum range • Supplementary Angles Equal ranges

Projectile Motion Type C - Partial or Asymmetric Parabola • Some problems can be treated as two Type A problems • Each problem is unique, so take your time and. . . stick to your major principles from the beginning

Projectile Motion y = voyt + 1/2 gt 2 Type C - Partial or Asymmetric Parabola Very Unique Equation We don’t know time, but we must find out the height (y) of an object.

Projectile Motion 1/2 gt 2 y = voyt + y = (vosin )t + 1/2 gt 2 Type C - Partial or Asymmetric Parabola Very Unique Equation vo voy = vosin vx = vocos

Projectile Motion 1/2 gt 2 y = voyt + y = (vosin )t + 1/2 gt 2 x = vxt x = (vocos )t x/(vocos ) = t Type C - Partial or Asymmetric Parabola Very Unique Equation vo voy = vosin vx = vocos

Projectile Motion 1/2 gt 2 y = voyt + y = (vosin )t + 1/2 gt 2 Type C - Partial or Asymmetric Parabola Very Unique Equation y = vosin (x/(vocos )) + 1/2 g(x/(vocos ))2 x/(vocos ) = t

Projectile Motion 1/2 gt 2 y = voyt + y = (vosin )t + 1/2 gt 2 Type C - Partial or Asymmetric Parabola Very Unique Equation y = vosin (x/(vocos )) + 1/2 g(x/(vocos ))2 y = x(sin /cos ) + 1/2 g(x 2/(vo 2 cos 2 )) y = xtan + 2 2 2 gx /(2 vo cos )

Projectile Motion 1/2 gt 2 y = voyt + y = (vosin )t + 1/2 gt 2 Type C - Partial or Asymmetric Parabola f o Very Unique Equation s e p y t l l a r o f s k r y. W =o vosin (x/(v!!ocos )) + 1/2 g(x/(vocos ))2 , s m e l prob ! ! C e p y 2/(v 2 cos 2 )) T h t i y = x(sin /cos ) + 1/2 g(x w l o u f e s u Most y = xtan + 2 2 2 gx /(2 vo cos )