LIMITI DI UNA FUNZIONE PRIMI CONCETTI ESEMPI INTRODUTTIVI

LIMITI DI UNA FUNZIONE • PRIMI CONCETTI • ESEMPI INTRODUTTIVI • DEFINIZIONI Prerequisiti : - funzioni - intorni

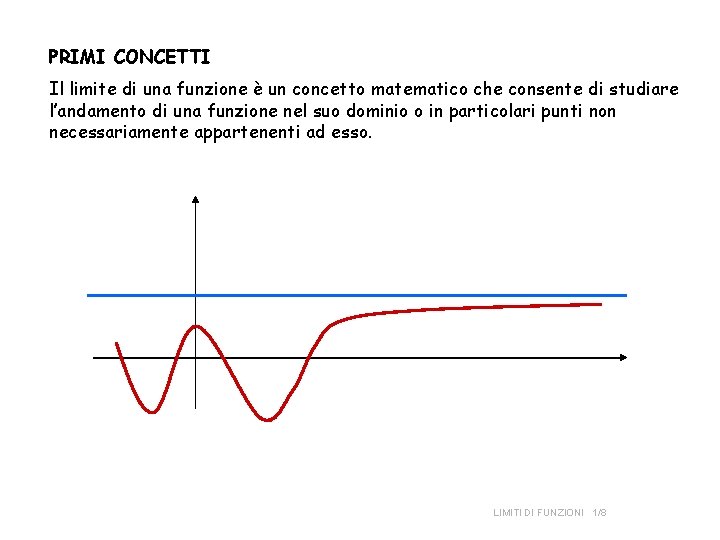
PRIMI CONCETTI Il limite di una funzione è un concetto matematico che consente di studiare l’andamento di una funzione nel suo dominio o in particolari punti non necessariamente appartenenti ad esso. LIMITI DI FUNZIONI 1/8

ESEMPI INTRODUTTIVI ESEMPIO 1/3 ESEMPIO 2/3 Assegnando alla x i valori 1, 2, 3, 4, 5, … osserviamo che i corrispondenti valori della funzione tendono al numero 1 senza mai oltrepassarlo Assegnando alla x valori prossimi a 1, la funzione tende ad assumere valori sempre più grandi x 1 2 3 f(x) 0 0, 5 0, 66 4 5 x . . . f(x) 0, 75 0. 8. . . 1, 2 1, 1 1, 08 1, 06 1, 04 1, 01. . . 5 10 12, 5 16, 6 25 100 ? ? Osservazione 1 Possiamo dire intuitivamente che la funzione, per valori della x ≥ 1 , ha un LIMITE che non può oltrepassare . . . Osservazione 2 Il valore x=1 non fa parte del dominio della funzione LIMITI DI FUNZIONI 2/8

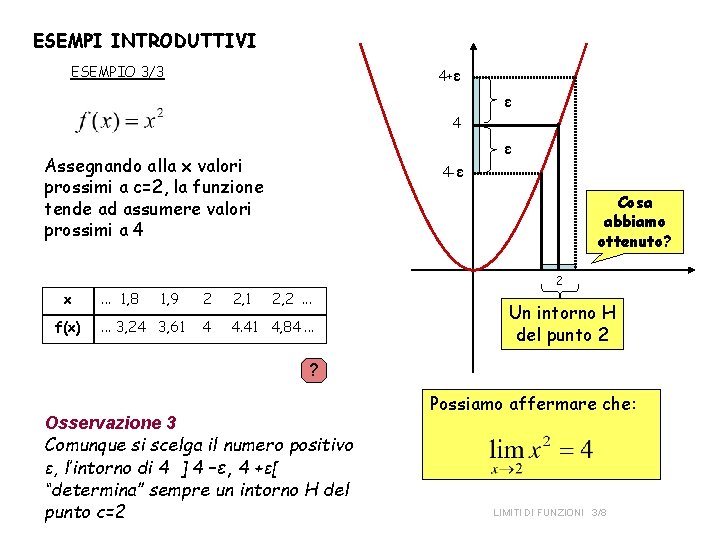
ESEMPI INTRODUTTIVI ESEMPIO 3/3 4+ε ε 4 ε Assegnando alla x valori prossimi a c=2, la funzione tende ad assumere valori prossimi a 4 4 -ε Cosa abbiamo ottenuto? 2 x f(x) . . . 1, 8 1, 9 . . . 3, 24 3, 61 2 2, 1 2, 2. . . 4 4. 41 4, 84. . . Un intorno H del punto 2 ? Osservazione 3 Comunque si scelga il numero positivo ε, l’intorno di 4 ] 4 –ε, 4 +ε[ “determina” sempre un intorno H del punto c=2 Possiamo affermare che: LIMITI DI FUNZIONI 3/8

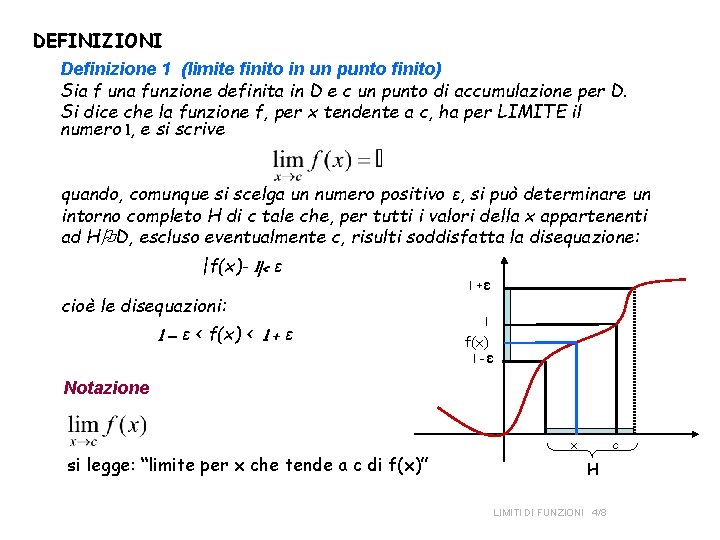
DEFINIZIONI Definizione 1 (limite finito in un punto finito) Sia f una funzione definita in D e c un punto di accumulazione per D. Si dice che la funzione f, per x tendente a c, ha per LIMITE il numero l, e si scrive quando, comunque si scelga un numero positivo ε, si può determinare un intorno completo H di c tale che, per tutti i valori della x appartenenti ad H D, escluso eventualmente c, risulti soddisfatta la disequazione: |f(x)- l|< ε cioè le disequazioni: l – ε < f(x) < l + ε l +ε l f(x) l -ε Notazione si legge: “limite per x che tende a c di f(x)” x c H LIMITI DI FUNZIONI 4/8

Definizione 2 (limite infinito in un punto finito) Sia f una funzione definita in D e c un punto di accumulazione per D. Si dice che la funzione f, per x tendente a c, ha per LIMITE l’infinto, e si scrive quando, comunque si scelga un numero positivo M, si può determinare un intorno completo H di c tale che, per tutti i valori della x appartenenti ad H D, escluso eventualmente c, risulti soddisfatta la disequazione: |f(x)| > M cioè le disequazioni: f(x) < -M f(x) > M In particolare, se vale: f(x) M c f(x) > M allora x -M H f(x) < -M allora LIMITI DI FUNZIONI 5/8

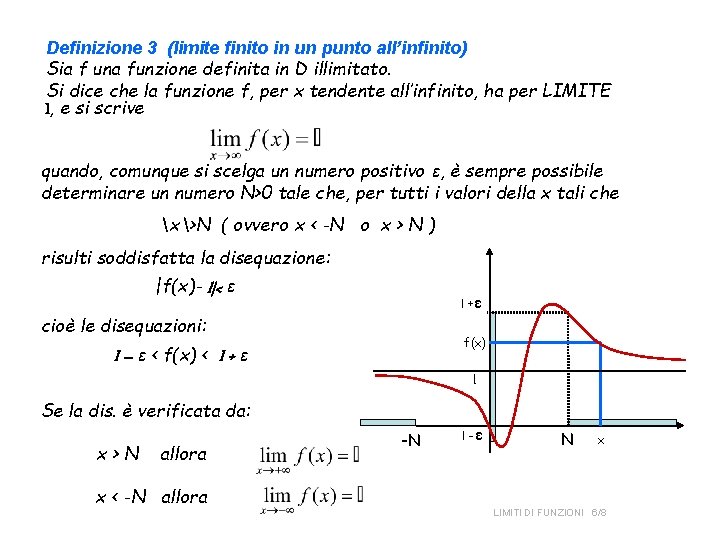
Definizione 3 (limite finito in un punto all’infinito) Sia f una funzione definita in D illimitato. Si dice che la funzione f, per x tendente all’infinito, ha per LIMITE l, e si scrive quando, comunque si scelga un numero positivo ε, è sempre possibile determinare un numero N>0 tale che, per tutti i valori della x tali che x>N ( ovvero x < -N o x > N ) risulti soddisfatta la disequazione: |f(x)- l|< ε l +ε cioè le disequazioni: f(x) l – ε < f(x) < l + ε l Se la dis. è verificata da: x>N allora x < -N allora -N l -ε N x LIMITI DI FUNZIONI 6/8

Definizione 4 (limite infinito in un punto all’infinito) Sia f una funzione definita in D illimitato. Si dice che la funzione f, per x tendente a , ha per LIMITE l’infinto, e si scrive quando, comunque si scelga M > 0, si può determinare N > 0 tale che, per tutti i valori della x tali che x>N risulti soddisfatta la disequazione: |f(x)| > M f(x) M cioè le disequazioni: f(x) < -M f(x) > M -N N x -M LIMITI DI FUNZIONI 7/8

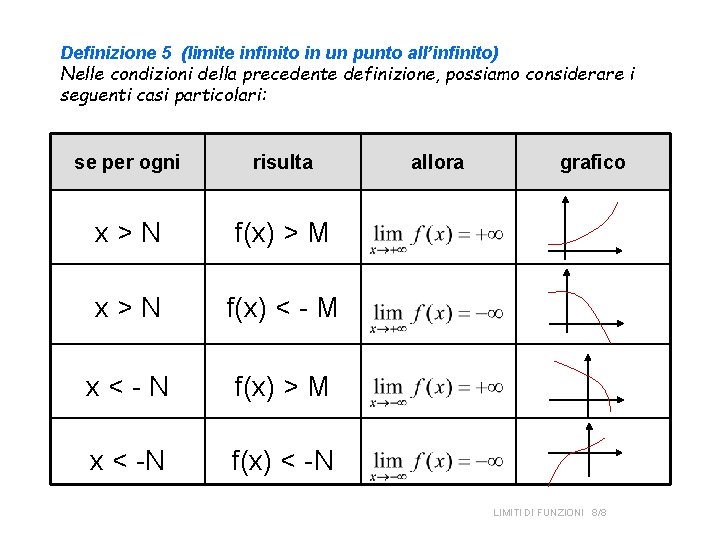
Definizione 5 (limite infinito in un punto all’infinito) Nelle condizioni della precedente definizione, possiamo considerare i seguenti casi particolari: se per ogni risulta x>N f(x) > M x>N f(x) < - M x<-N f(x) > M x < -N f(x) < -N allora grafico LIMITI DI FUNZIONI 8/8