Lesson 7 Magnetic Fields Magnetic Force on moving












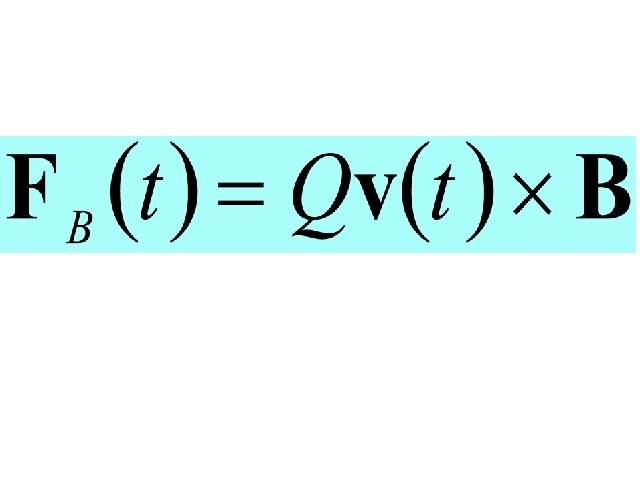



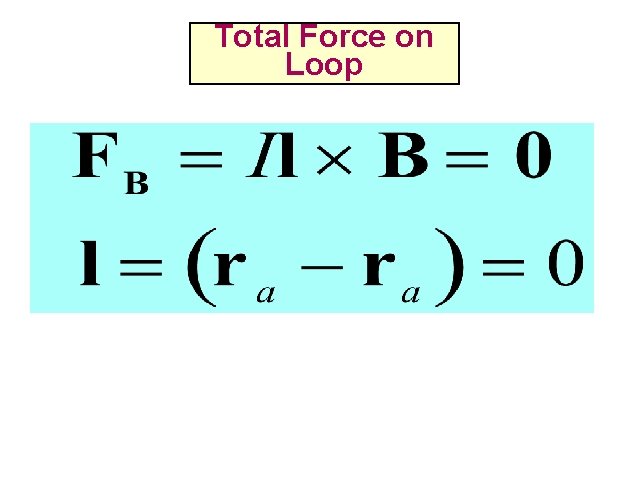
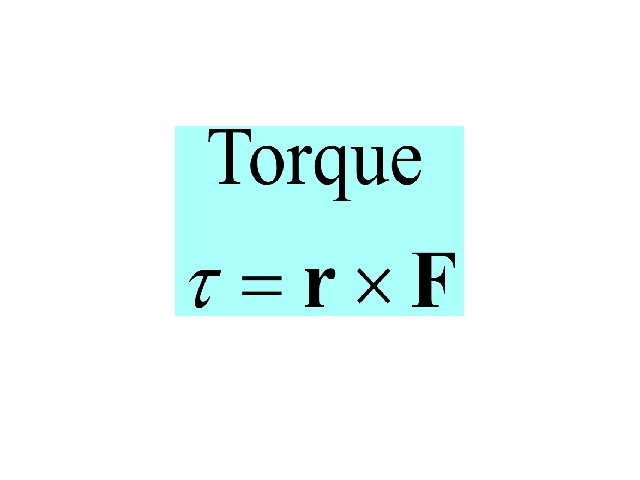




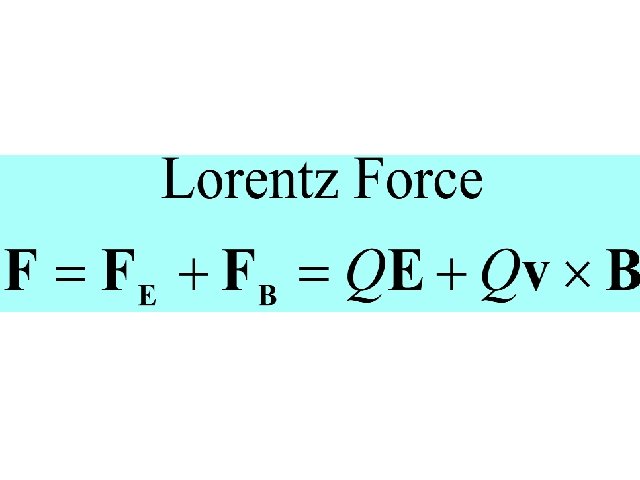
- Slides: 34

Lesson 7 Magnetic Fields áMagnetic Force on moving charge áMotion of charge in Magnetic Field áMagnetic Force on current carrying conductor áTorque on current carrying loop áHall Effect áMagnetic Devices

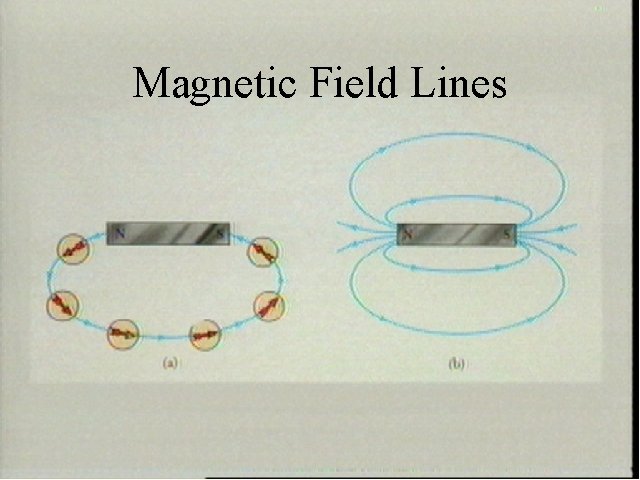
Magnetic Force áSome metallic objects cause other metallic objects to accelerate áThus must be producing a force áThis force is different to Gravitational Force and Electric Force áCan plot the directions of lines field #By alignment of magnetic dipoles áMAGNETIC FORCE

Magnetic Field Lines

áProperties of Magnetic Fields #Moving charge (current) is effected q. Force proportional Q and v q. FB = 0 if v parallel to Magnetic Field B q. FB perpendicular to v and B q. FB on positive charge opposite to that on negative charge q. FB proportional to Sin of the angle v makes with B

Mathematical Expression

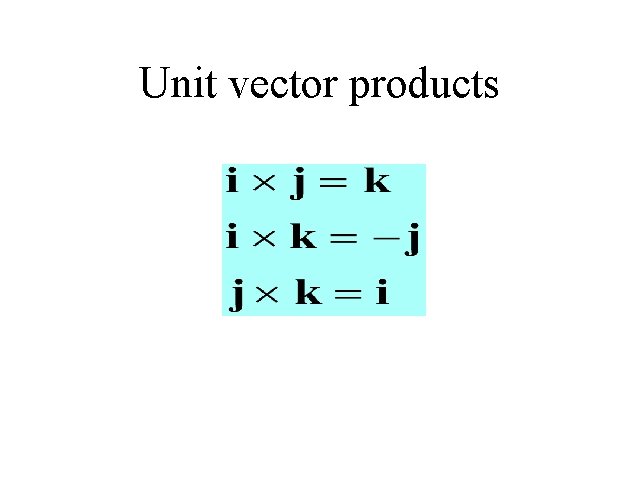
Vector Product I Vector Product A = Ax i + Ay j + A z k B = B x i + By j + Bz k i A ´ B = Ax Bx j Ay By k Ay Az = By Bz Az Ax i. Bz Bx Ax Az j+ Bx Bz Ay k By = ( A y B z - A z B y )i - ( A x B z - A z B x ) j + ( A x B y - A y B x )k

Vector Product II A ´ B = -B´ A A´A =0 A ´ B = 0 Þ A parallel to B A ´ B = ( AB )Sin (q ) A ´ B = AB if A is perpendicular to B A ´ B is perpendicular to A and B

Unit vector products

Work done by Magnetic Work Done by Magnetic Force � on. Field charge d. W B = F B · d s = (Q v ´ B ) · d s = 0 As v ´ B is perpendicular to v and B and v is parallel to d s

Compare to Electric Force Work done by Electric Field

¨Thus Kinetic Energy of charge is not changed by FB Implications ¨Potential Energy is not changed 1 2 1 DK = m vf - m vi 2 2 Þ vi = vf i. e. speed is constant under influence of but v can change direction 2 =0 B

SI units

Magnetic Flux FB Magnetic Flux For constant magnetic field Bover flat area with area vector A F B = B · A=ABcosq in general FB = [F ] = B ò B · d. A surface Tm = Wb (Weber ) 2

Right Hand Rule for Magnetic Force

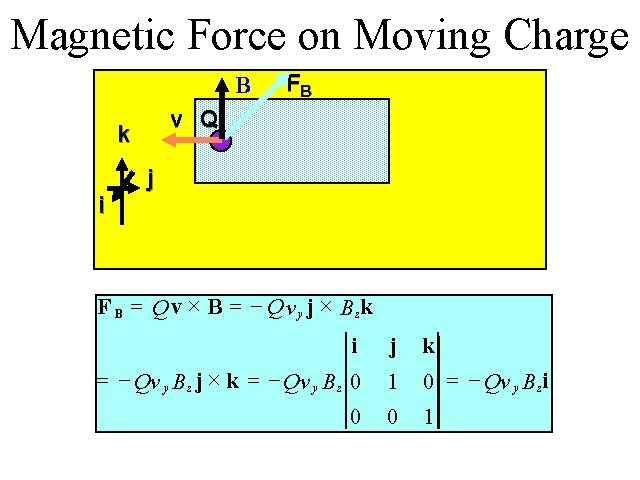
Magnetic Force on Moving Charge B v Q k i FB j F B = Q v ´ B = - Q v y j ´ Bzk i j k = - Qv y B z j ´ k = - Qv y B z 0 1 0 = - Qv y B z i 0 0 1
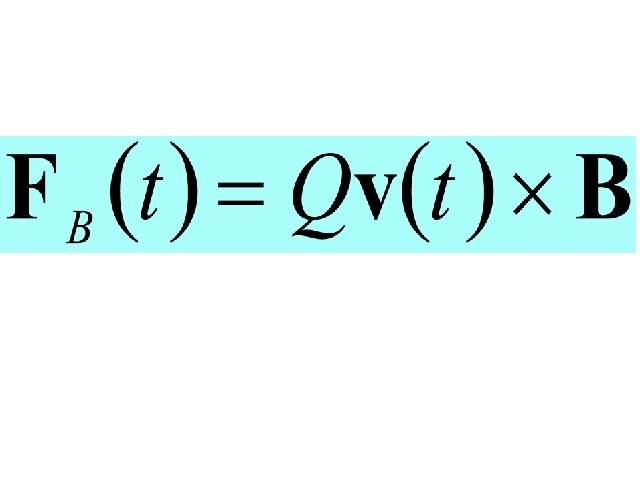
Mathematical expression

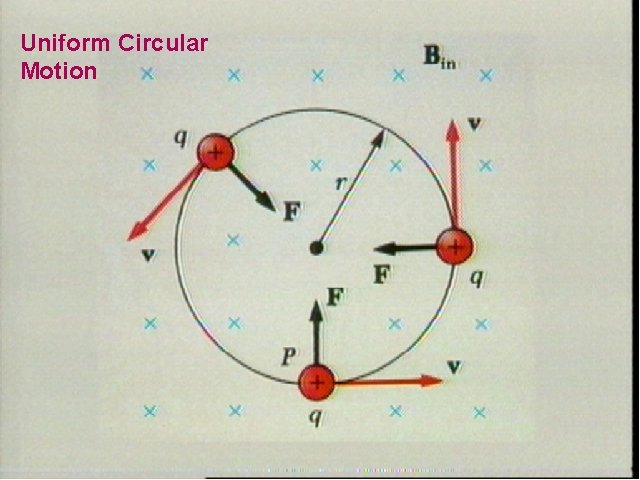
Uniform Circular Motion of Charge

2 F v Qv. B = = ac = r m m 2 mv Þ = Qv. B r mv = r radius of motion QB v = rw Mathematical analysis w = BQ angular speed = angular freqency ( rad ) s m w BQ = = f frequency (cps = Hz ) 2 pm pm 1 2 T = = period of the motion. f BQ

Magnetic Bottles magnetic bottles

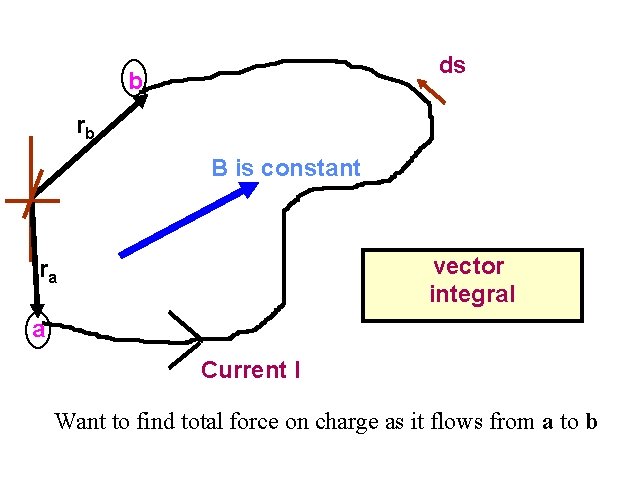
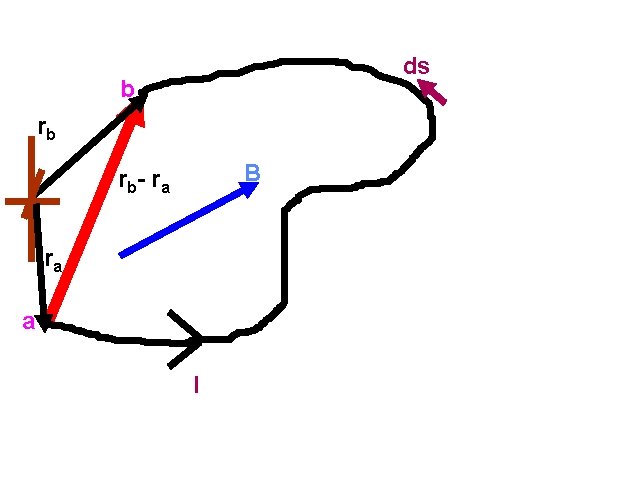
Force. Magnetic on current carrying conductor in Force on Current a uniform constant magnetic field: FB = I ò a b d s ´ B = Il ´ B l = (r b - r a ) é ù æ d. Q ö ds sˆ = ç ds ÷ sˆ = ( I ds ) sˆ = I d s ú ê d. Q v = d. Q è dt ø ë û dt where

b ds Vector Integral I rb B is constant vector integral ra a Current I Want to find total force on charge as it flows from a to b

b ds Vector Integral II rb B rb - r a ra a I

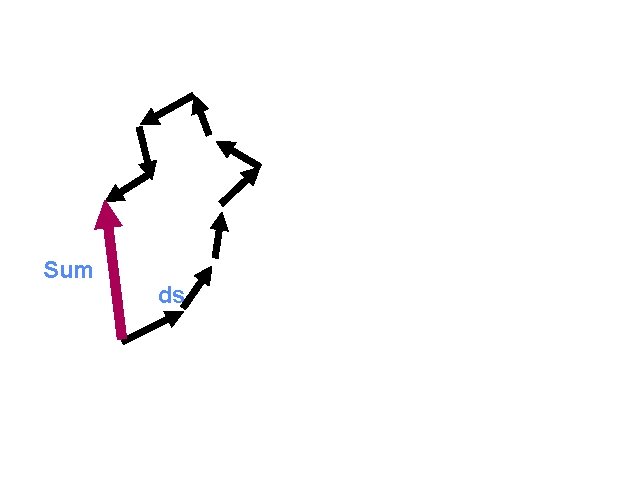
Vector Integral III Sum ds

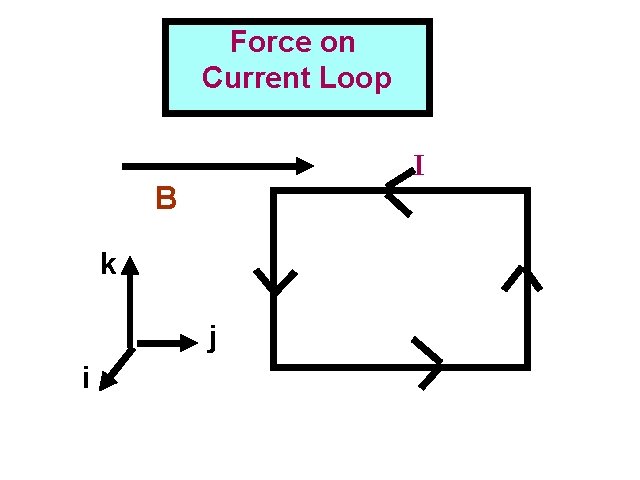
Force on Magnetic Force on Current Loop I I B k j i
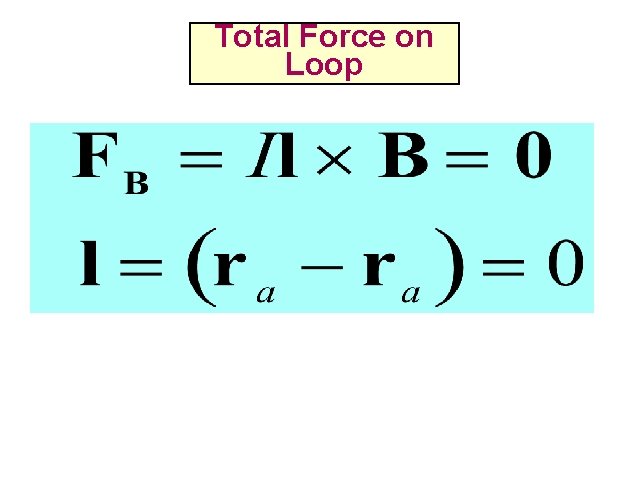
Total Force on Magnetic Force Loop on Current Loop II

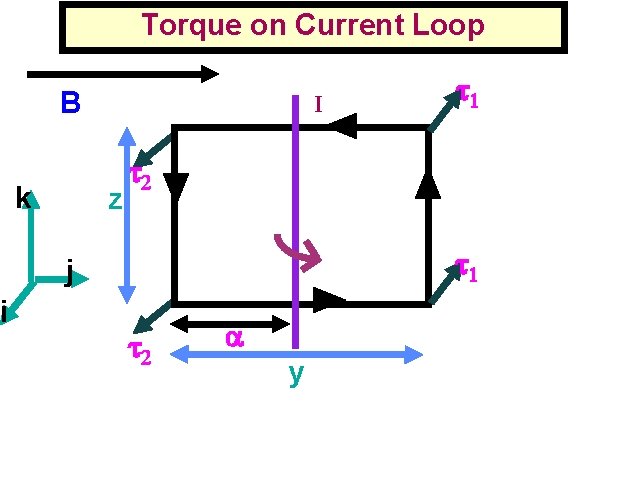
i Torque on Current Loop I I B k z j y
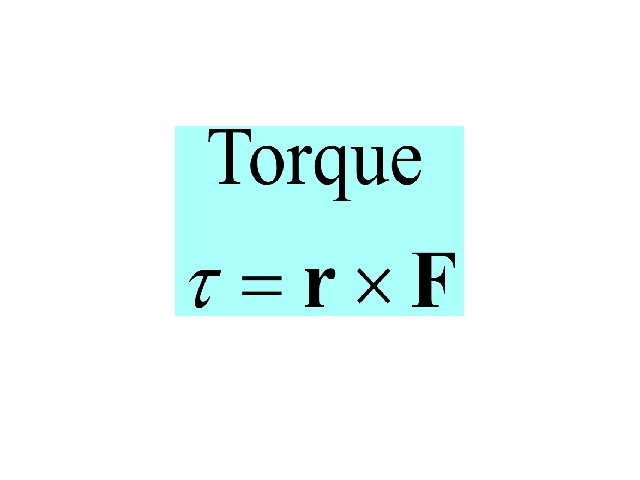
Torque on Current Loop II

Torque on Current Loop III

Magnetic Moment Torque on Current Loop in yz plane in a uniform magnetic field in positive y direction t = IABk In general the torque on a current loop in magnetic field is t = M´B M = IA, where A is the area vector of the loop with the orientation given by the current flow , .

A=Ai: Area vector with Oriented Area Vector orientation I k j i A

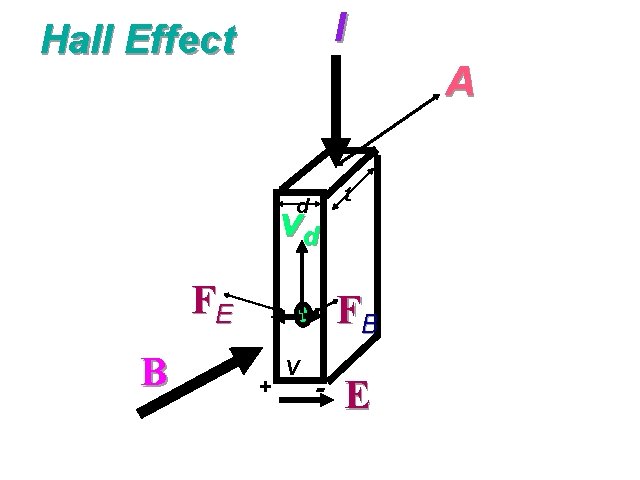
I Hall Effect A d vd FE B t FB + V - E

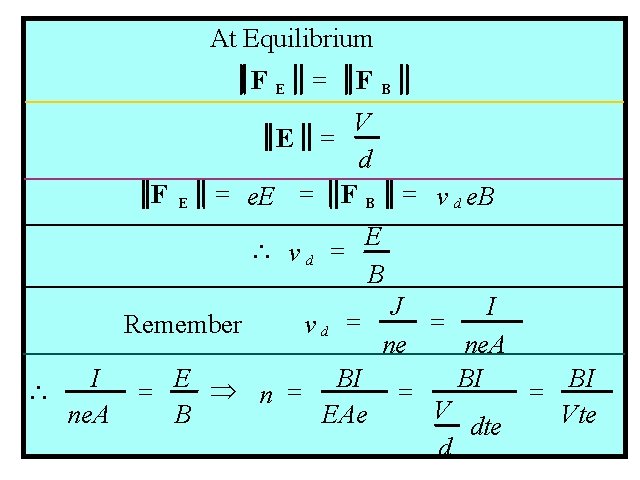
At Equilibrium FE = FB Mathematical analysis F E V E = d = e. E = F B = v d e. B vd = E B J I = Remember vd = ne ne. A I = E Þ BI = BI BI = = n V ne. A B EAe Vte d

Measurement can measure vd by measuring the PD V.
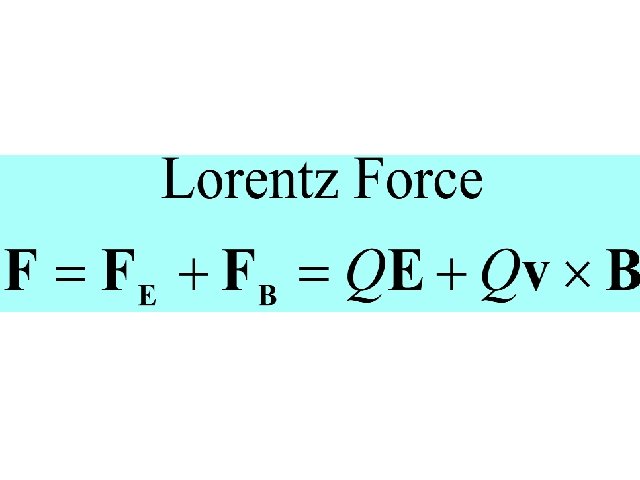
Lorentz Force