Les classifieurs linaires Classifieurs linaires Classifieurs linaires Les

















- Slides: 22

Les classifieurs linéaires

Classifieurs linéaires

Classifieurs linéaires Les fonctions discriminantes peuvent être autres que linéaires (même philosophie) Pourquoi des fonctions discriminantes linéaires ? Modèle simple et facilement solvable analytiquement. Optimale pour les distributions gaussiennes avec une même matrice de covariance (cours précédent) Pas optimale pour d’autres distribution mais relativement efficace. Ne demande pas d’autres types d’information (modèle de probabilités…)

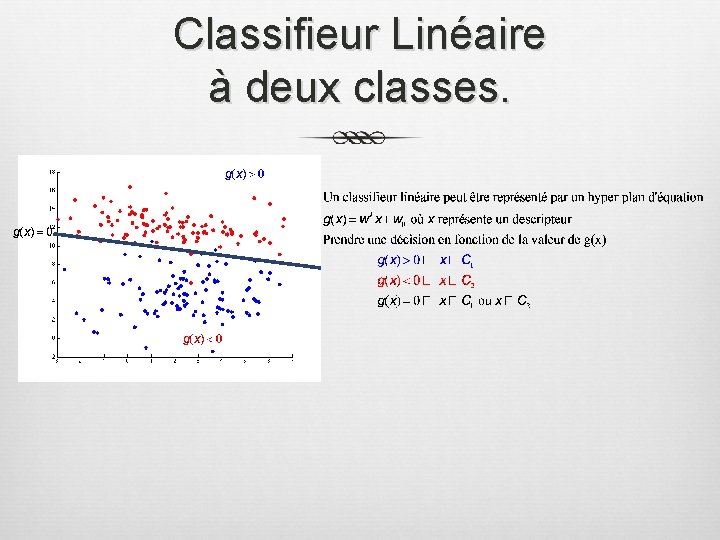
Classifieur Linéaire à deux classes.

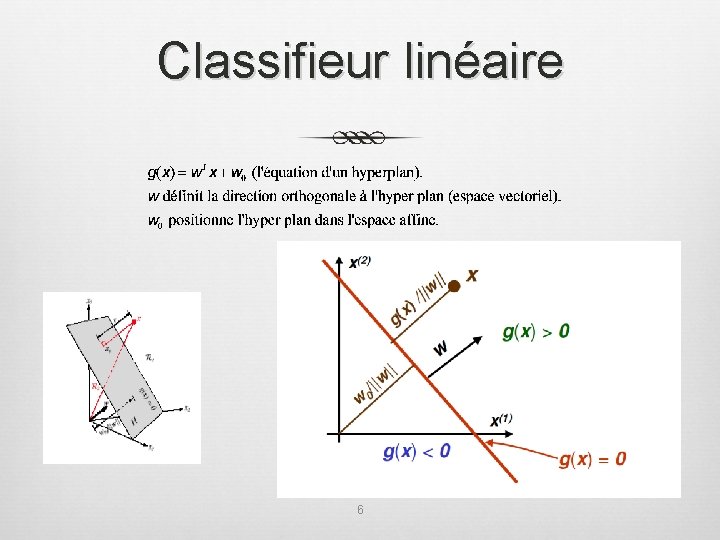
Classifieur linéaire

Classifieur linéaire 6

Classifieurs linéaires

Classifieurs linéaires

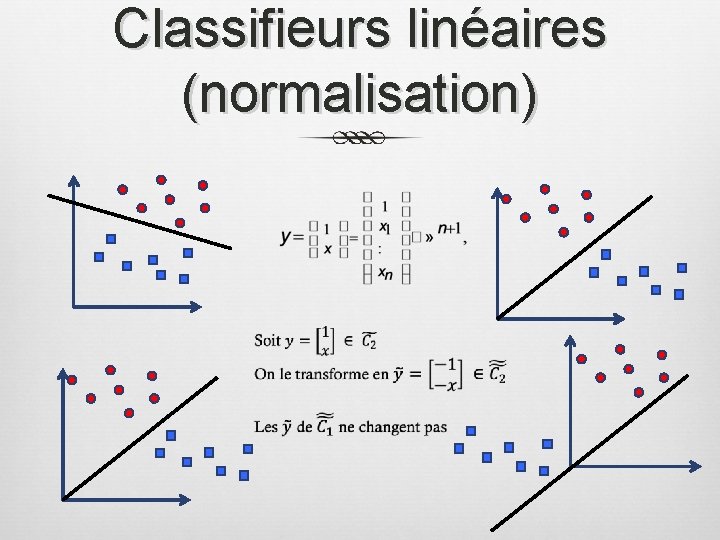
Classifieurs linéaires (normalisation)

Classifieurs linéaires (normalisation) On a les propriétés suivantes :

Classifieurs linéaires (normalisation)

Définir un critére J(W) Les points verts sont mal-classés.

Définir un critére J(W) On peut alors définir l’ensemble des mal classés par W Les points verts sont mal-classés.

Allégement de la notation

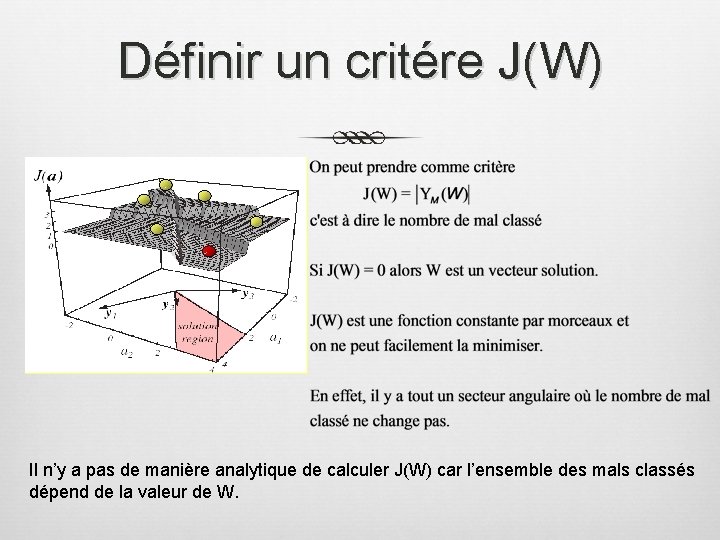
Définir un critére J(W) Il n’y a pas de manière analytique de calculer J(W) car l’ensemble des mals classés dépend de la valeur de W.

Définir un critére J(W)

Perceptron

Perceptron

Fonctionnement du Perceptron Est-ce qu’il faut que la descente de gradient soit amortie ? • Si la descente de gradient est amortie a t-on la bonne solution ? Si le problème n’est pas linéairement séparable que se passe-t-il ? • Si la descente de gradient n’est pas amortie.

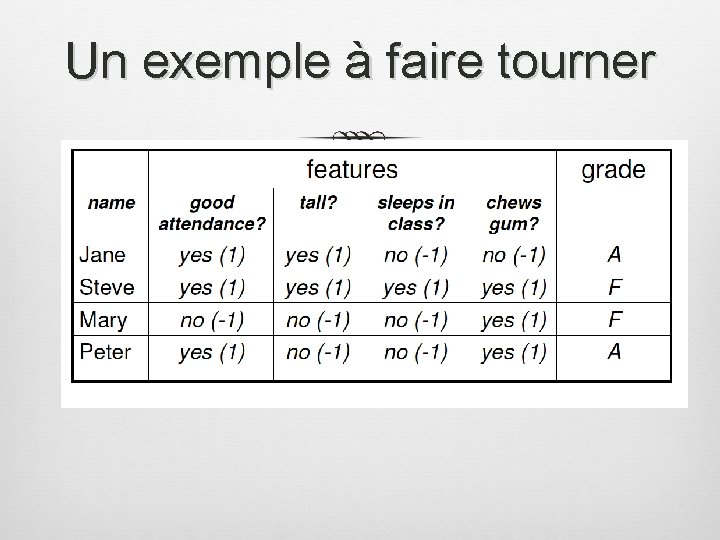
Un exemple à faire tourner


Un autre exemple Une classe d’apprentissage C 1 est représentée par les éléments suivants : { C 11 = (1, 5) ; C 13 = (3, 3) ; } Une classe d’apprentissage C 2 est représentée par les éléments suivants : { C 21=(2, 1) ; C 22 = (3, 2) ; } • • • Expliquer et formaliser la méthode du perceptron sur ces données (équation, propriété de la solution dans le cas d’un problème linéairement séparable, augmentation en dimension des données et modification en fonction de l’appartenance à la classe). Faire tourner l’algorithme jusqu’à convergence, on calculera le gradient en utilisant l’ensemble de tous les mal classés. On initialisera l’algorithme avec le vecteur [-1 ; -4 ; -2]. A quelle classe appartiendra le point C = (6, 4) ? Justifier votre réponse.
 Olivier linaires
Olivier linaires Prix des linaires
Prix des linaires Les trois obstacles et les quatre démons
Les trois obstacles et les quatre démons Les actionneurs et les préactionneurs
Les actionneurs et les préactionneurs Je moi tu toi
Je moi tu toi Les mots qu'on ne dit pas sont les fleurs du silence
Les mots qu'on ne dit pas sont les fleurs du silence Trouvez les réponses. écrivez-les en chiffres (numbers).
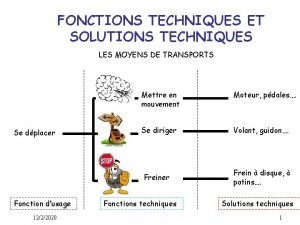
Trouvez les réponses. écrivez-les en chiffres (numbers). Fonctions techniques
Fonctions techniques Le volcan le plus dangereux du monde
Le volcan le plus dangereux du monde Un appel vient pour des soldats
Un appel vient pour des soldats Les parts de les plantes
Les parts de les plantes Pour commencer organisateur textuel
Pour commencer organisateur textuel Les voyages en train grand corps malade explication
Les voyages en train grand corps malade explication Les voitures les plus rapides du monde
Les voitures les plus rapides du monde La ficelle présentation
La ficelle présentation L'horloge stratégique
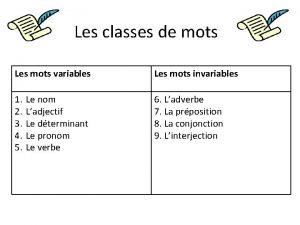
L'horloge stratégique Mots variables et invariables
Mots variables et invariables Parts d'una flor
Parts d'una flor Cestbeaulavie
Cestbeaulavie Allez vous en sur les places
Allez vous en sur les places Les constellations les plus connues
Les constellations les plus connues J'aime les bouches sans venin les cœurs sans stratagème
J'aime les bouches sans venin les cœurs sans stratagème Savantement
Savantement