Lenguaje matemtico El lenguaje de las matemticas es


















- Slides: 20




Lenguaje matemático El lenguaje de las matemáticas es un lenguaje difícil para la persona que no es matemática. Y con mucha frecuencia, incluso para quienes trasmiten el conocimiento matemático, se confunde el algoritmo de un procedimiento matemático con lenguaje matemático. El lenguaje matemático tiene una capacidad de síntesis y de profundo significado que permite el avance de la matemática per se, y permite el avance en el estudio de la naturaleza. El lenguaje, todo lenguaje por lo general, se expresa mediante palabras (lenguaje oral) y mediante símbolos (lenguaje escrito) Este símbolo significa literalmente: “para todo” El lenguaje matemático por símbolos es “casi” universal. Todo matemático traduce inmediatamente este símbolo “ para todo” en la forma correcta, aunque lo pronuncie en polaco, inglés o español.

Lenguaje matemático A menudo leímos o escuchamos el discurso: “…saludamos a todos y cada uno de ustedes…”. Desde el punto de vista formal del lenguaje matemático hay una redundancia en esta expresión. Si el saludo es para todos entonces cada uno lo recibe, y viceversa, si saludamos a cada uno entonces todos reciben el saludo. Con esto queremos ejemplificar que el lenguaje matemático tiene la característica de ser riguroso, esto es no permite la ambigüedad y la redundancia. El lenguaje matemático es, por lo general, incomprensible para quien no haya estudiado la matemática, y esto arrastra una desgracia (para quien no ha aprendido el lenguaje): “la matemática es muy complicada”. Esta notación, que representa un concepto fundamental para el desarrollo de la ciencia fue creada formalmente en 1666 (annus mirabilis de Isaac Newton), y ha sido fundamental para el avance de la humanidad. Cuidado, muchas veces la simbología utilizada en el lenguaje matemático, produce un rechazo y dificulta en el umbral de la enseñanza el aprendizaje de la matemática

Lenguaje matemático Para enseñar matemática no se debe, necesariamente, enseñar desde el principio el lenguaje matemático, y luego entonces la matemática. Debe ser el propio estudiante quien, por la regularidad o patrones inherentes a la mayoría de los procedimientos matemáticos, se de cuenta de la necesidad de un lenguaje propio que debe tener la matemática. Si iniciamos una clase sobre funciones cuadráticas diciendo: “una función cuadrática es una expresión de la forma Ax 2 + Bx + C”, creo que es una vertiente a una enseñanza “conductista” que ha mostrado su fracaso en la enseñanza de la matemática en Chile. Por otro lado, hay un cierto lenguaje matemático que mediante su simbología sencilla, se ha incorporado al lenguaje popular: “hay n cantidad de gente” traduciéndose por “mucha gente”. “Multiplícate por cero”, forma tajante de decir “desaparece de mi vista”. La “corrupción en Chile ha crecido exponencialmente”, entendiendo con esto que el crecimiento exponencial es un crecimiento extremadamente rápido. “No te preocupes el orden de los factores no altera el producto”, utilizando la propiedad conmutativa de la multiplicación para justificar cierta desidia o desorden en el quehacer jerárquico de algún procedimiento casero.

Lenguaje matemático Por otro lado, el propio lenguaje cotidiano ha dado ropaje al lenguaje matemático. Las palabras “cerrado”, “abierto”, “compacto”, “acumulación”, de claro significado en el diccionario, es utilizado, en virtud de la imagen asociadas a esas palabras, conceptos de alta complejidad en la topología, una rama de la matemática. Las lenguas griegas, latinas, árabes, hebreas han hecho su aporte fundamental. En particular el alfabeto griego prácticamente ha prestado todas sus letras para denominar los ángulos de un triángulo, para denotar ciertas funciones muy frecuentes y de alta complejidad en matemáticas. La historia y hechos trágicos en la humanidad han contribuido para formar la simbología del lenguaje en la matemática. El ejemplo paradigmático es la estructura de “Espacio Polaco”, en homenaje a todos los matemáticos polacos perseguidos o asesinados por el régimen Nazi en la segunda Guerra Mundial.

Lenguaje matemático Lo cotidiano y el lenguaje matemático: Usted va en su automóvil y le pregunta a un niño pequeño de 5 o 6 años (su hijo, nieto o sobrino) y le dice: tengo 5 manzanas y me como tres manzanas, ¿cuántas manzanas me quedan? Seguro que después de agregar y quitar dedos dirá: ¡ 2 manzanas! Si usted, al mismo pequeño, le pone en un papel la simbología abstracta: con seguridad no sabrá que responder… ¡Sabe restar pero no sabe el lenguaje matemático ! Ni soñar con esperar la respuesta al problema en lenguaje matemático: A los doce o trece años, este chico con seguridad dará la respuesta y dirá: 3 m Pero existe el riesgo de que olvide que m representa manzanas, o cualquiera otra unidad física…

Lenguaje matemático La anécdota anterior no es trivial. A menudo nos preocupamos en exceso en la operación algebraica simbólica olvidando el contexto: “Si tengo cinco manzanas y me como dos…” Vamos a insistir en este exceso… El cuadrado de un binomio Se haya o no verificado que el alumno rezará este hermosísima expresión como un “credo”: El cuadrado de un binomio es igual al cuadrado del primer término, más el doble del primero por el segundo, y más el cuadrado del segundo término.

Lenguaje matemático Será complicado para un profesor dar una aplicación de esta fórmula mediante “manzanas”. Incluso si se le pudiera ocurrir decir que si a = 5 y b =2 entonces cuanto vale (a + b)2, toda vez que con seguridad más de un alumno aplicará la ley del mínimo esfuerzo y sumará 5 + 2 que es 7 y luego dará con la respuesta: ¡ 49! Con seguridad, continuará con problemas consistente en entregar una ristra de letras donde el estudiante deberá tener la habilidad de encontrar, al igual que en un puzle de letras, otra ristra de letras que se puedan compactar a la expresión de un binomio al cuadrado o en algún otro “producto notable” Si los alumnos pasan esta prueba, entonces aparecerán ingeniosas operaciones para mezclar el cuadrado del binomio con otras potencias, como por ejemplo,

Lenguaje matemático Sea como sea, las dos clases de ejercicios anteriores no han dado respuesta a la pregunta ¿para qué sirve el cuadrado de un binomio? El cuadrado de un binomio, ejemplo de belleza en el lenguaje de la matemática El cuadrado rojo es de lado a, y el cuadrado azul es de lado b. ¿Cuánto vale el área de la superficie encerrada en verde?

Lenguaje matemático El cuadrado rojo es de lado a, y el cuadrado azul es de lado b. ¿Cuánto vale el área de la superficie encerrada en verde? Con estos ejemplos queremos decir que el inicio de la enseñanza del lenguaje matemático debería ir acompañado de modelos didácticos que refuercen y permitan entender este lenguaje. Un lenguaje tipo “Bourbaki” es dañino para la enseñanza de la matemática en los primeros años de escolaridad (K-10)

Lenguaje matemático El cuadrado del Binomio y el cuadrado de 1: una belleza práctica p q p p 2 pq q 2 ½ ½ ½ ¼ ¼ 1/3 2/3 1/9 2/3 2/9 4/9

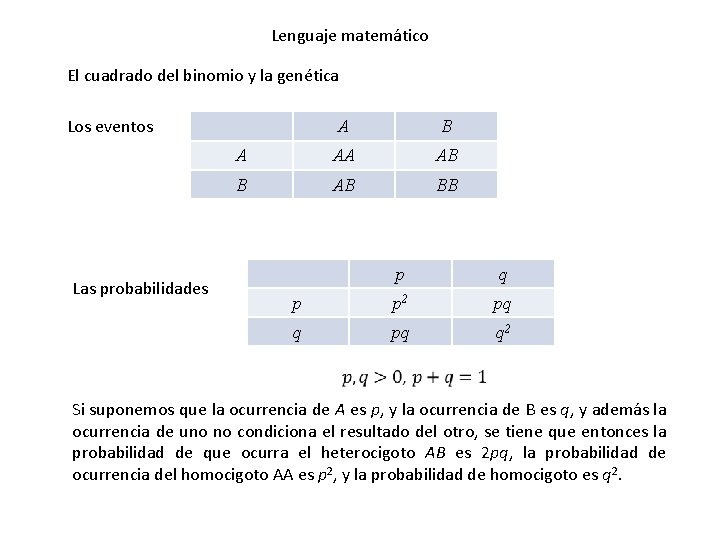
Lenguaje matemático El cuadrado del binomio y la genética Los eventos Las probabilidades A B A AA AB BB p q p p 2 pq q 2 Si suponemos que la ocurrencia de A es p, y la ocurrencia de B es q, y además la ocurrencia de uno no condiciona el resultado del otro, se tiene que entonces la probabilidad de que ocurra el heterocigoto AB es 2 pq, la probabilidad de ocurrencia del homocigoto AA es p 2, y la probabilidad de homocigoto es q 2.

Lenguaje matemático Con los modelos didácticos anteriores para (a + b)2 queremos hacer énfasis que el lenguaje matemático debe estar adherido a un contexto, y que el lenguaje matemático sirve para la construcción de modelos matemáticos. En nuestro caso, el cuadrado del binomio nos ha servido para explicar prácticamente las Leyes de la Genética, con el equilibrio Weinberg-Hardy incluido. Y además se le ha dado un sentido geométrico a la expresión (a + b)2 asociado al cálculo de áreas de superficies, así como la descomposición del 1 en factores positivos que serán de gran aplicación en la teoría de la probabilidad elemental en los últimos dos años del sistema K-12. Un lenguaje, cualquiera que sea, por muy riguroso y formal que sea a veces no puede escapar de una mala interpretación. Veremos un ejemplo de interpretación que puede acarrear ciertas dificultades en el aprendizaje de la matemática que aprenden los pequeños de sistema K-6, la tabla de multiplicar

Lenguaje matemático: La Tabla de Multiplicar En CHile, Holanda, E: E: UU: la tabla de multiplicar es… A esta tabla la llamaremos tabla(3)-1

A esta tabla la llamaremos tabla(3)-2

Lenguaje matemático: La Tabla de Multiplicar Si a un pequeño le “ayudamos” a que recuerde la tabla del 3 diciéndole: “si sabes que 3 x 2 es 6, entonces 3 x 3 es el mismo resultado anterior pero le sumas 3, esto es 3 x 3 = 9, y en consecuencia si quieres saber cuanto es 3 x 4, al resultado anterior le sumas 3, y entonces obtendrás que 3 x 4 = 12… La pregunta que surge, entonces… el lenguaje descrito en la tabla(3)-1 ¿es concomitante con el razonamiento anterior? La respuesta será negativa, y para hacerla positiva debemos escudarnos en la “conmutatividad del producto”. Sin embargo, la enseñanza de la “conmutatividad del producto” arrastra otro problema epistemológico, puesto que la definición de m x n = n +. . . + n (m sumandos) adoptada por Chile, o la adoptada por Japón m x n = m + … + m (n sumandos) en un contexto didáctico no es tan trivial la conmutatividad, salvo que utilicemos la técnica de “a fortiori” (es así porque es así)

tabla(3)-1 En esta tabla no se suma 3, la tabla de multiplicar chilena tabla(3)-2 En esta tabla se suma 3, la tabla de multiplicar japonesa

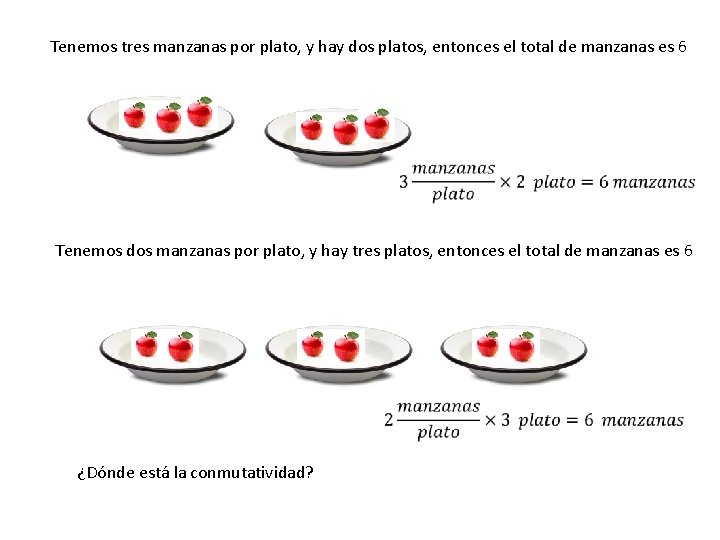
Tenemos tres manzanas por plato, y hay dos platos, entonces el total de manzanas es 6 Tenemos dos manzanas por plato, y hay tres platos, entonces el total de manzanas es 6 ¿Dónde está la conmutatividad?
 Jose uno de los operarios registro adicionalmente
Jose uno de los operarios registro adicionalmente Matemticas
Matemticas Lenguaje ordinario y lenguaje algebraico ejemplos
Lenguaje ordinario y lenguaje algebraico ejemplos Lenguaje algebraico ejemplos
Lenguaje algebraico ejemplos (a-b)^2 lenguaje verbal
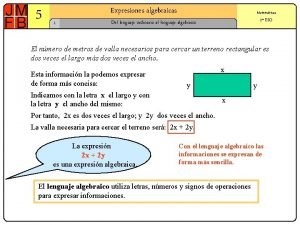
(a-b)^2 lenguaje verbal Tema 5 expresiones algebraicas 2 eso
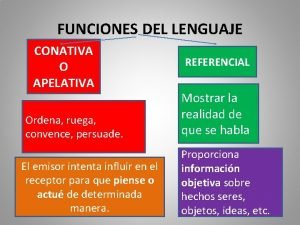
Tema 5 expresiones algebraicas 2 eso Funciones del lenguaje
Funciones del lenguaje Funcion referencial comentario de texto
Funcion referencial comentario de texto Metalinguistica
Metalinguistica Lengua de la mariposa
Lengua de la mariposa Proposiciones de lenguaje
Proposiciones de lenguaje Cuadro sinoptico de las funciones del lenguaje
Cuadro sinoptico de las funciones del lenguaje El lenguaje complementario de las palabras es
El lenguaje complementario de las palabras es Cuaderno en cuantas silabas se divide
Cuaderno en cuantas silabas se divide Cuadro comparativo entre las niif plenas y las niif pymes
Cuadro comparativo entre las niif plenas y las niif pymes Tamaño de celulas
Tamaño de celulas Linea de tiempo de las generaciones de las computadoras
Linea de tiempo de las generaciones de las computadoras Dicen que las palabras se las lleva el viento
Dicen que las palabras se las lleva el viento Las misiones se hacen
Las misiones se hacen Generacion de computadoras
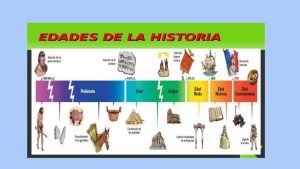
Generacion de computadoras Las edades de la historia
Las edades de la historia