Lecture 3 Vector fields Phasors and why we








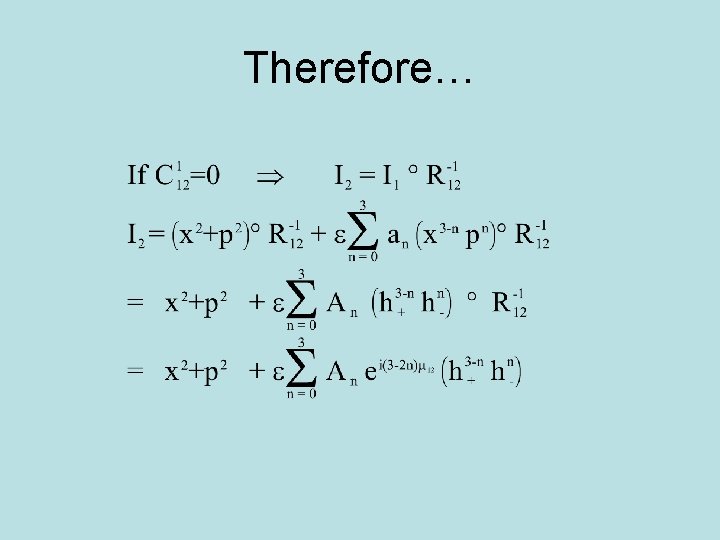




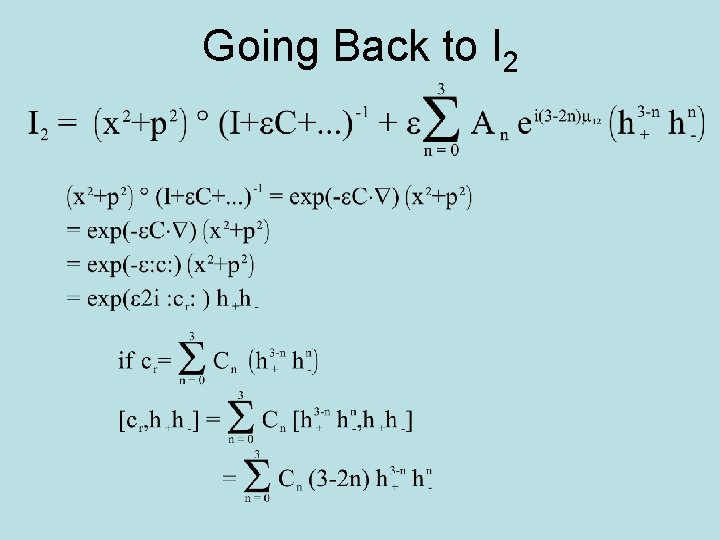






- Slides: 24

Lecture 3 Vector fields, Phasors and why we care! a. Description of our goals

Question • What was the quintessential (典型的な{て んけいてき ) message of Lecture 2?

Exercise Of Lectures 1 1. 2. 3. 4. Use Complex Taylor series! Use the anti-derivative Use an inverse DAMAP and compute it with a vector field!

What is our practical goal? • We can turn phase plots into circles exactly in the linear case • We can turn phase plot formally in the nonlinear case • In the linear case, we saw how this gives us a method to compute Lattice functions • BIG QUESTION: Even if we could make circles in the nonlinear case, is that what accelerator physics is all about? Turning ellipses, Lissajou figures and other oddities into circles?

If we were mathematicians? • Yes, if we were mathematicians, turning a complex phase plot into a circle would be an end into itself! Mathematicians would declare our system “integrable” and “uninteresting”! • But we are not mathematicians! Many lattices which can be made into circles or other simple normal forms maybe unacceptable to us!

Goal: Understanding the Defects of a Lattice • For example, a lattice may be perfect (according to design), as far as the linear properties are concerned. • But, the aperture is small and the phase space deformed because of nonlinearities • What is a good way to look at this?

Answer: Normalize the part we already understand like • Transform lattice by the linear A • The normalized data is a circle if linear • Deviation from circularity is the result of an annoying nonlinearity • Study these troubling distortions: how do they propagate and how can they be erased

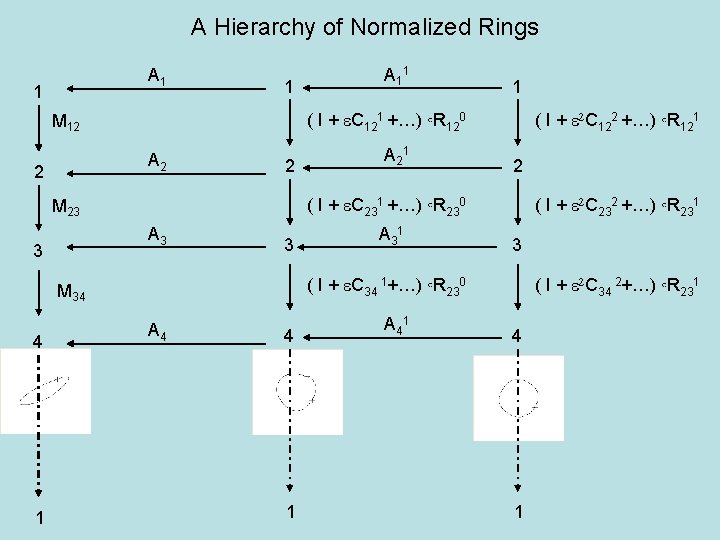
A Hierarchy of Normalized Rings A 1 1 1 A 2 2 A 3 3 1 2 A 31 ( I + e 2 C 232 +…) ◦R 231 3 ( I + e. C 34 1+…) ◦R 230 M 34 4 A 21 ( I + e 2 C 122 +…) ◦R 121 ( I + e. C 231 +…) ◦R 230 M 23 3 1 ( I + e. C 121 +…) ◦R 120 M 12 2 A 11 A 4 4 1 A 41 ( I + e 2 C 34 2+…) ◦R 231 4 1

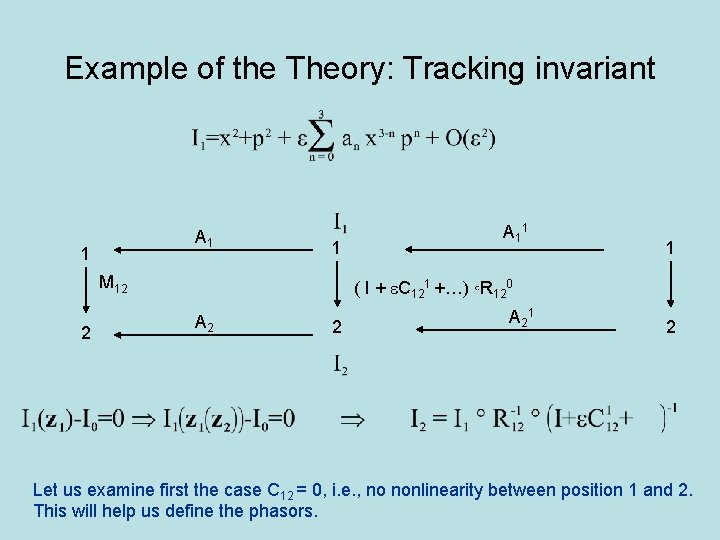
Example of the Theory: Tracking invariant A 1 1 1 M 12 2 A 11 1 ( I + e. C 121 +…) ◦R 120 A 2 2 A 21 2 Let us examine first the case C 12 = 0, i. e. , no nonlinearity between position 1 and 2. This will help us define the phasors.

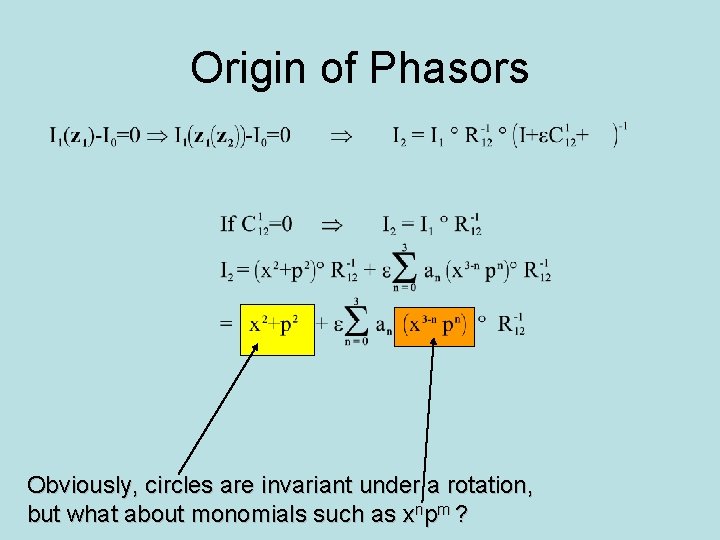
Origin of Phasors Obviously, circles are invariant under a rotation, but what about monomials such as xnpm ?

Phasor Definition

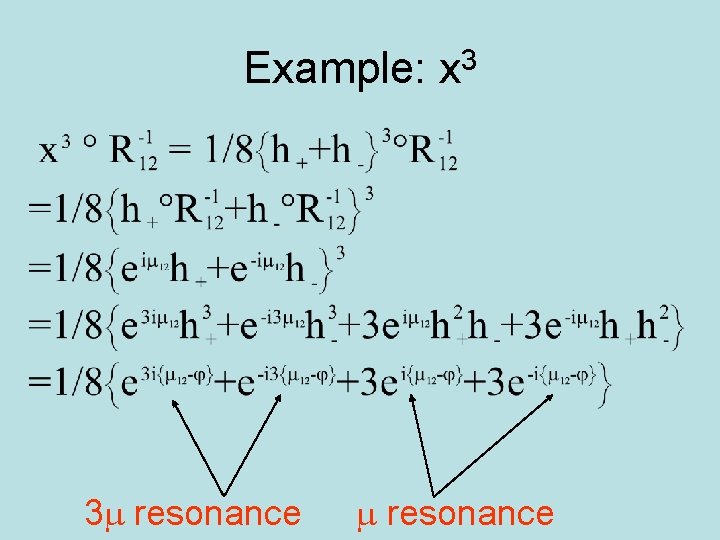
Example: x 3 3 m resonance
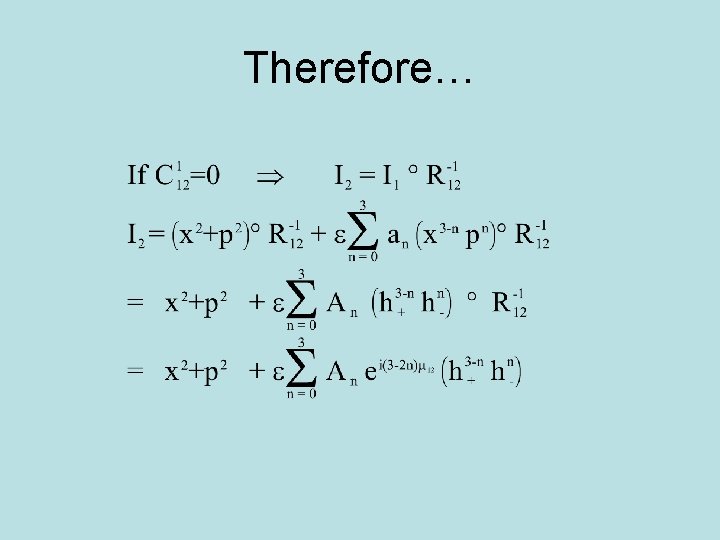
Therefore…

The other term: C 121≠ 0 • For any map near the identity map, such as M=I+εC, the substitution operation into a function f defined as: • Mf ≡ f ◦ M can be rewritten as Mf = exp(εĈ • ∇) f Where Ĉ=C+O(ε 2)

Hamiltonian Case • If the map M=I+εC is derived from a Hamiltonian, then: Mf = exp(εĈ • ∇) f = exp(ε: c: ) f Where c is a function of x and p and : c: acts on an arbitrary function f as by taking a Poisson Bracket: : c: f = [c, f] = ∂x c ∂p f - ∂p c ∂x f or Ĉ = (- ∂p c , ∂x c )

Simple Examples • Translation: T= exp(: w: )= exp(W • ∇) w=-tx p + tp x ; W = (tx, tp ) • • • Linear part of Drift : D= exp(: d: )= exp(D • ∇) d= -L p 2/2 D=(Lp, 0) Sextupole Kick : S= exp(: s: )= exp(S • ∇) s=-ks L x 3 ; S = (0, - ks L x 2) Rotation of angle μ: R = exp(-μ: c: ) c= (x 2+p 2)/2 and Ĉ= (-p, x) Courant-Snyder Matrix c= (γ x 2+2αxp+βp 2)/2 Damping Map: Xnew = (ea X, ea P) D = exp(D • ∇) D= (a, a) : d: does not exist NOT HAMILTONIAN MAP Integer resonance unstable fixed point Xnew = (ea X, e-a P) D= (a, -a) d= -a xp

Rotation is Easy in Terms of Phasors • Application of Phasors: Notice that [h+ , h-] =-2 i. Thus in phasor space, the Poisson Bracket of two functions f ang g is given by {f , g} = -2 i (∂+ f ∂- g - ∂- f ∂+ g) = -2 i [f , g] R = exp( iμ: h+h-: )
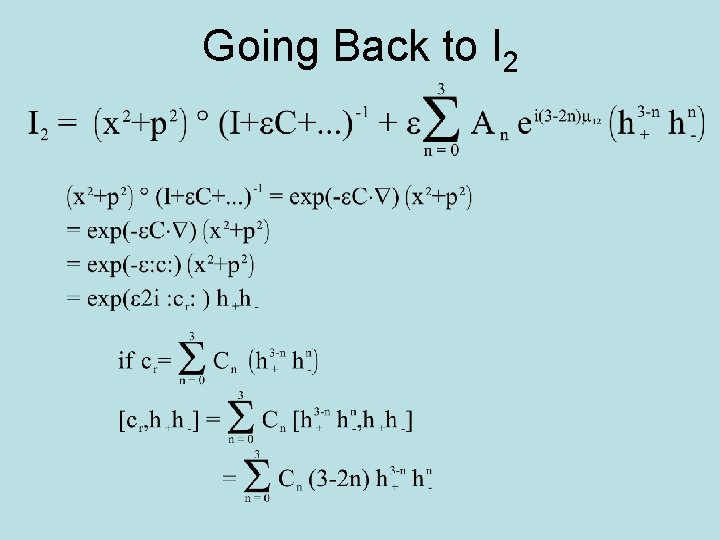
Going Back to I 2

Final Expression

1 ( I + e. C 12 1 +…) ◦R 12 0 Now we can construct one turn map in the first Floquet ring 2 ( I + e. C 231 +…) ◦R 230 3 ( I + e. C 34 1+…) ◦R 230 4 M 11=…( I + e. C 34 1+…) ◦R 230 ◦ ( I + e. C 231 +…) ◦R 230 ◦ ( I + e. C 121 +…) ◦R 120 M 11 = R 120 exp( e. C 121 • ∇) R 230 exp( e. C 231 • ∇) R 340 exp( e. C 341 • ∇)… 1 M 11 = exp( e (R 120 C 121+ R 130 C 231+…) • ∇) R 0

Resonances and Distortions • A resonance is an abnormality of phase space. • A distortion is an unacceptable deviation from linearity (or mid-plane symmetry) but the map is still a rotation in disguise.

Pictures Resonance: in blue Distortion

Start with Resonance • Globally Ms=As◦R◦As-1 is impossible. • Globally Ms=As◦N◦As-1 such that N=R 2 p/3◦N◦R 2 p/3 -1 is possible.

One-Resonance Normalization
 Red fields
Red fields Adding phasors
Adding phasors Addition and subtraction of phasors
Addition and subtraction of phasors Phasor notation
Phasor notation Vector resolution
Vector resolution Hey hey bye bye
Hey hey bye bye Dividing phasors
Dividing phasors Phasors electrical engineering
Phasors electrical engineering Steady state sinusoidal analysis using phasors
Steady state sinusoidal analysis using phasors Phasor notation
Phasor notation 01:640:244 lecture notes - lecture 15: plat, idah, farad
01:640:244 lecture notes - lecture 15: plat, idah, farad Formula for partitioning a line segment
Formula for partitioning a line segment Vector unitario de un vector
Vector unitario de un vector Is position vector
Is position vector Don't ask why why why
Don't ask why why why Electric forces and fields concept review
Electric forces and fields concept review We plough the fields and scatter modern version
We plough the fields and scatter modern version Rodan and fields tax write offs
Rodan and fields tax write offs Learning: module 26: magnetic forces and fields
Learning: module 26: magnetic forces and fields Magnets and magnetic fields lesson 1 answer key
Magnets and magnetic fields lesson 1 answer key Chapter 16: electric forces and fields answers
Chapter 16: electric forces and fields answers Solve the following riddles
Solve the following riddles Maxwell equations for time varying fields
Maxwell equations for time varying fields 3 branches of psychology
3 branches of psychology Conceptual physics chapter 33
Conceptual physics chapter 33