Instituto Tecnolgico do Sudoeste Paulista Faculdade de Engenharia

Instituto Tecnológico do Sudoeste Paulista Faculdade de Engenharia Elétrica – FEE Bacharelado em Engenharia Elétrica Aula 1 Equilíbrio Mecânico de Corpos Rígidos Física Geral e Experimental II Prof. Ms. Alysson Cristiano Beneti IPAUSSU-SP 2012

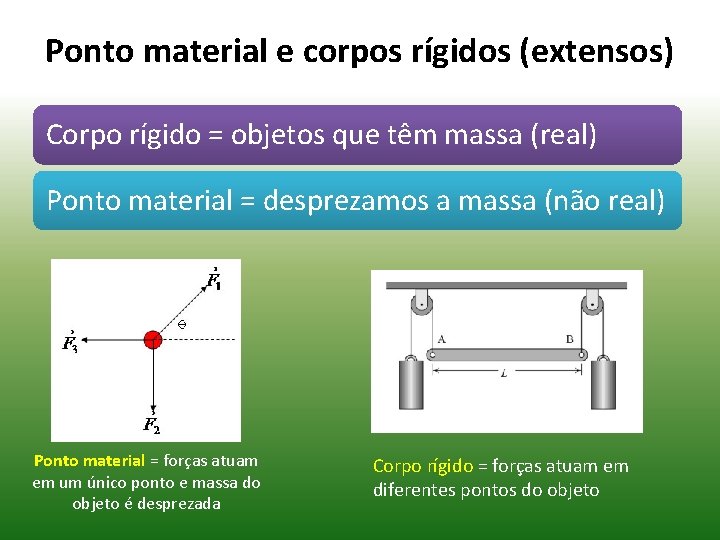
Ponto material e corpos rígidos (extensos) Corpo rígido = objetos que têm massa (real) Ponto material = desprezamos a massa (não real) Ponto material = forças atuam em um único ponto e massa do objeto é desprezada Corpo rígido = forças atuam em diferentes pontos do objeto

Tipos de movimento Translação = movimentos em linha reta ou aproximadamente reta (curvas suaves). Ex: carro em movimento, tiro (projétil em movimento), Terra em torno do Sol. . . Rotação = movimentos em torno de um eixo que está localizado no objeto. Ex: carrossel, rotação da Terra, disco de vinil e CD, roda da bicicleta. . .

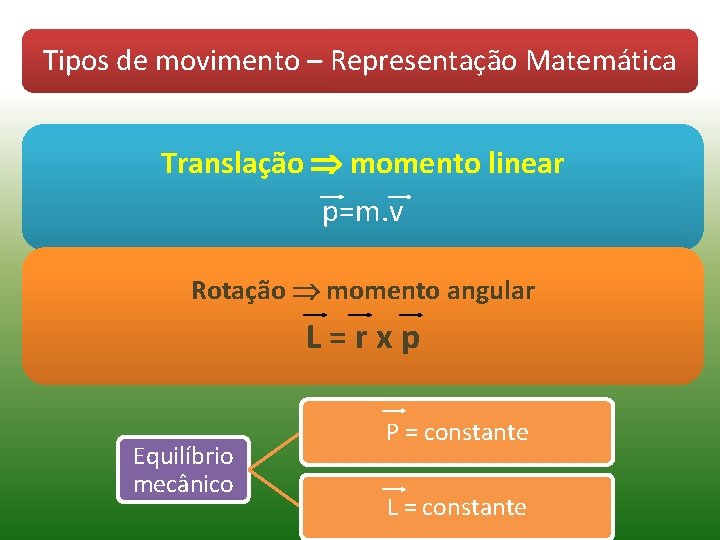
Tipos de movimento – Representação Matemática Translação momento linear p=m. v Rotação momento angular L=rxp Equilíbrio mecânico P = constante L = constante

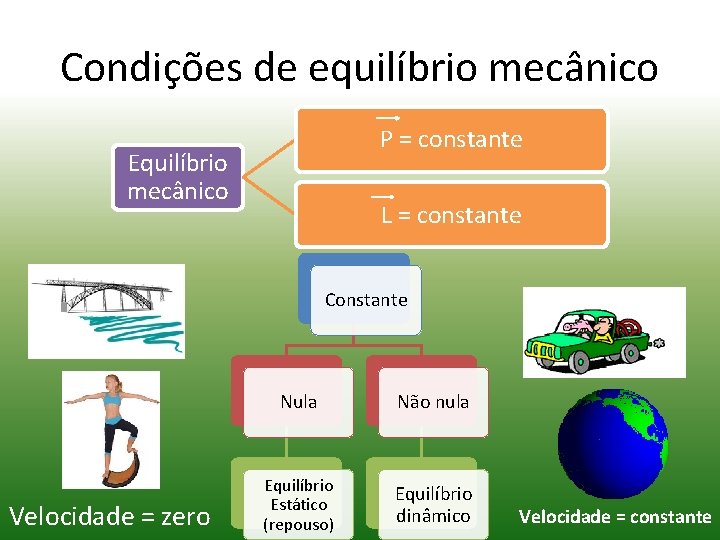
Condições de equilíbrio mecânico P = constante Equilíbrio mecânico L = constante Constante Velocidade = zero Nula Não nula Equilíbrio Estático (repouso) Equilíbrio dinâmico Velocidade = constante

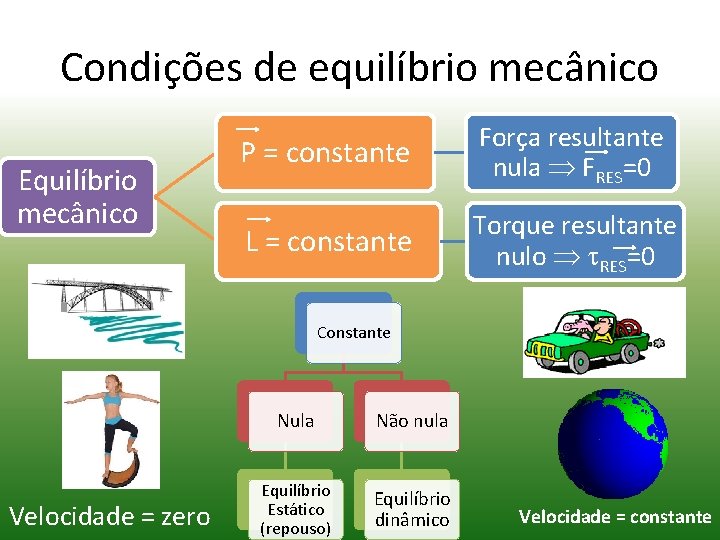
Condições de equilíbrio mecânico Equilíbrio mecânico P = constante Força resultante nula FRES=0 L = constante Torque resultante nulo RES=0 Constante Velocidade = zero Nula Não nula Equilíbrio Estático (repouso) Equilíbrio dinâmico Velocidade = constante

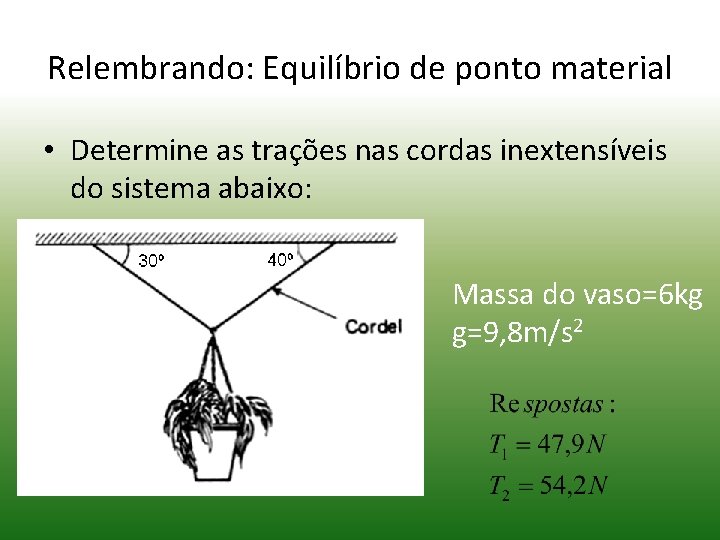
Relembrando: Equilíbrio de ponto material • Determine as trações nas cordas inextensíveis do sistema abaixo: Massa do vaso=6 kg g=9, 8 m/s 2

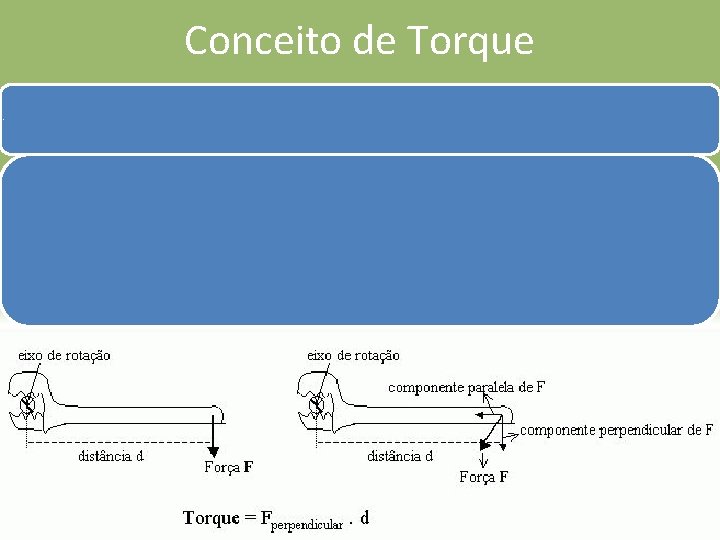
Conceito de Torque (táu) representa torque. É uma grandeza vetorial É uma grandeza que representa a rotação de um objeto (ou sistema) em torno do seu próprio eixo, considerando sua massa e a distância de aplicação da força em relação ao eixo.

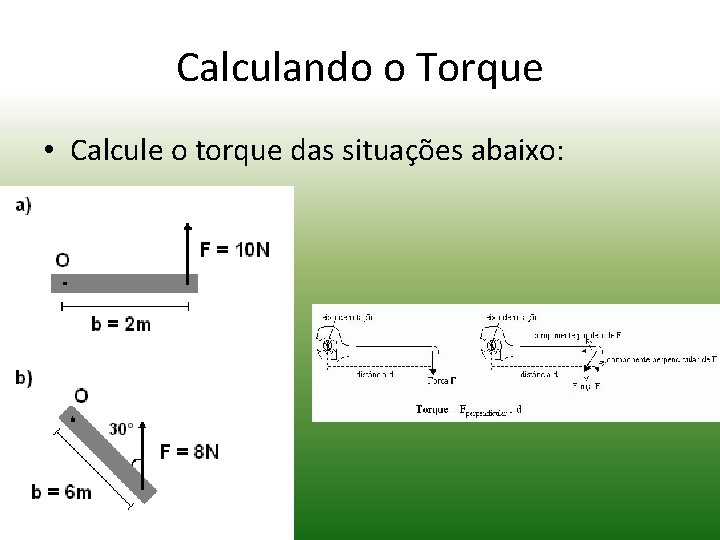
Calculando o Torque • Calcule o torque das situações abaixo:

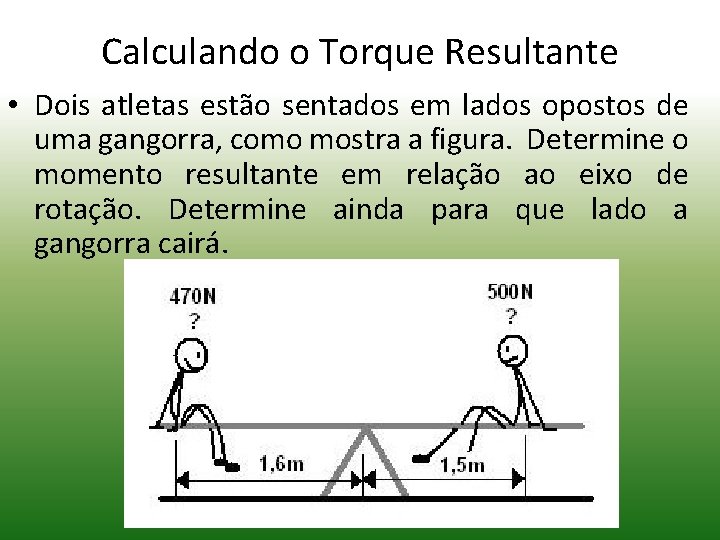
Calculando o Torque Resultante • Dois atletas estão sentados em lados opostos de uma gangorra, como mostra a figura. Determine o momento resultante em relação ao eixo de rotação. Determine ainda para que lado a gangorra cairá.