I Previously on IET Complex Exponential Function ImAxis


- Slides: 23

I. Previously on IET

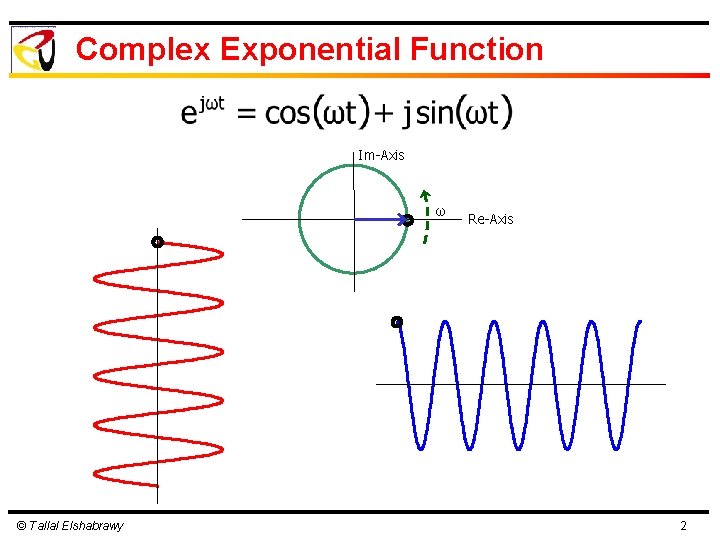
Complex Exponential Function Im-Axis ω © Tallal Elshabrawy Re-Axis 2

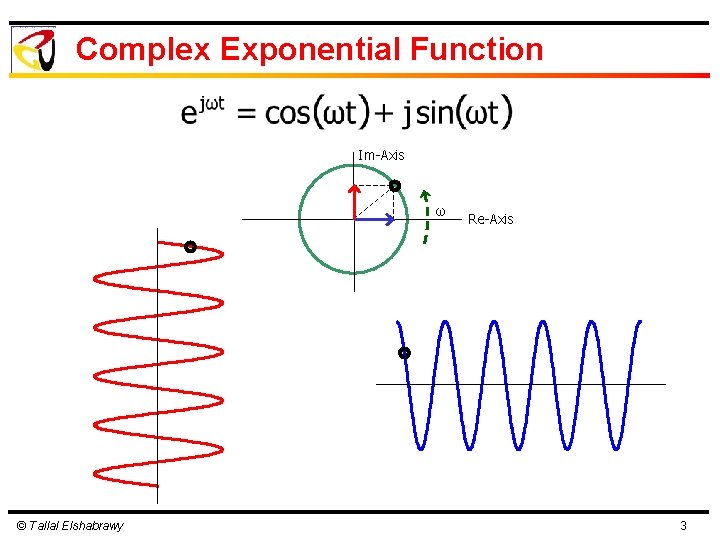
Complex Exponential Function Im-Axis ω © Tallal Elshabrawy Re-Axis 3

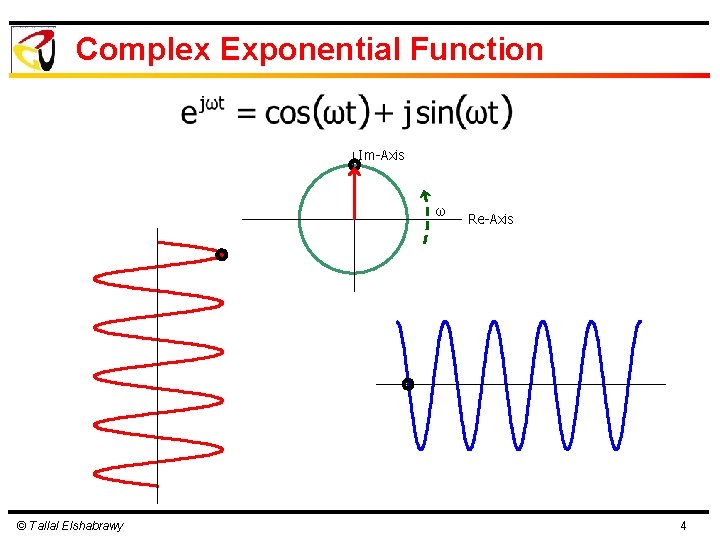
Complex Exponential Function Im-Axis ω © Tallal Elshabrawy Re-Axis 4

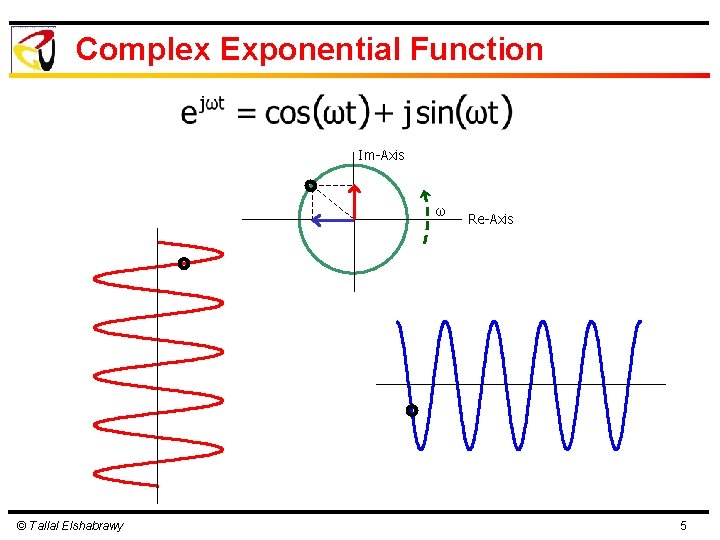
Complex Exponential Function Im-Axis ω © Tallal Elshabrawy Re-Axis 5

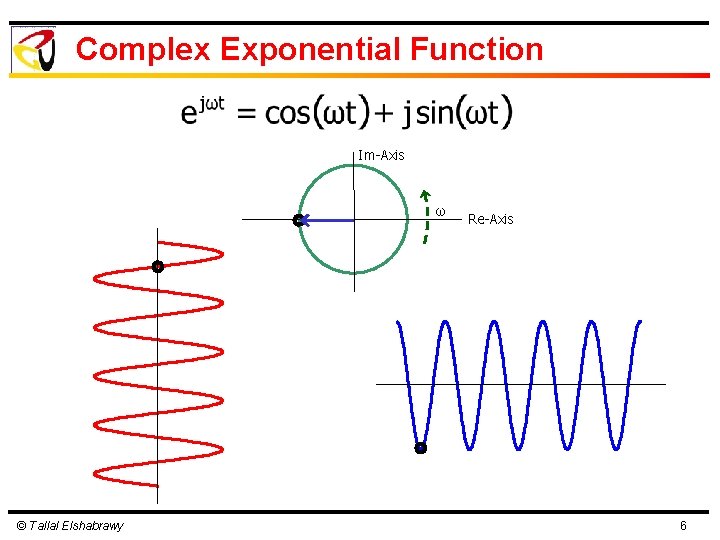
Complex Exponential Function Im-Axis ω © Tallal Elshabrawy Re-Axis 6

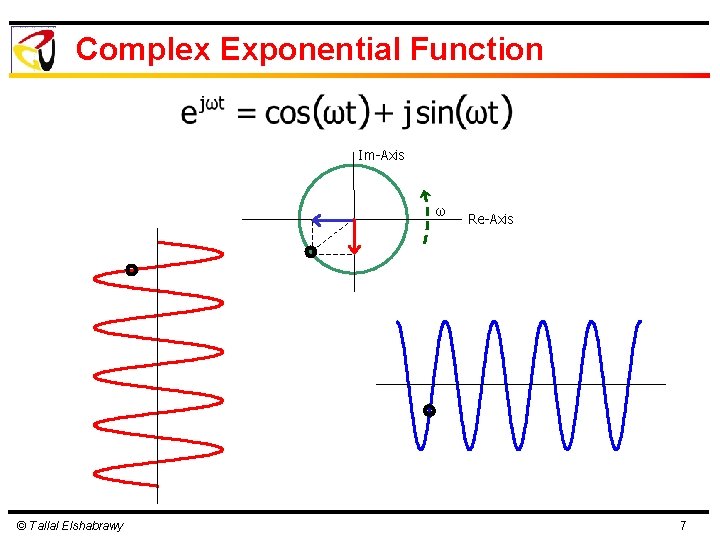
Complex Exponential Function Im-Axis ω © Tallal Elshabrawy Re-Axis 7

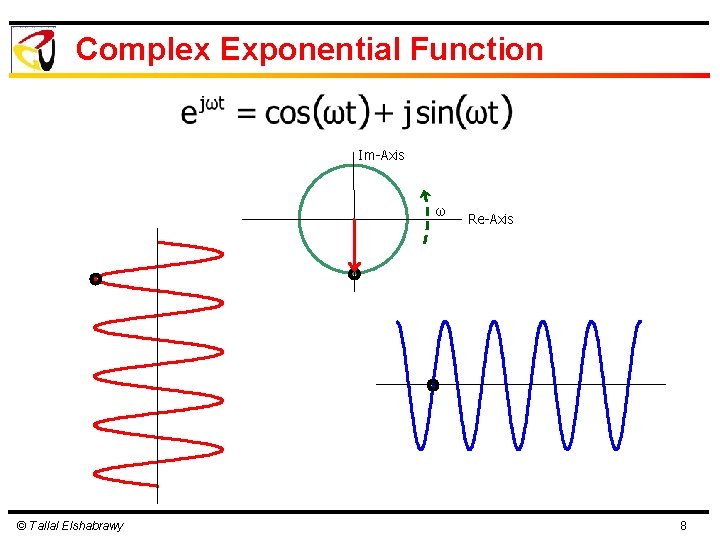
Complex Exponential Function Im-Axis ω © Tallal Elshabrawy Re-Axis 8

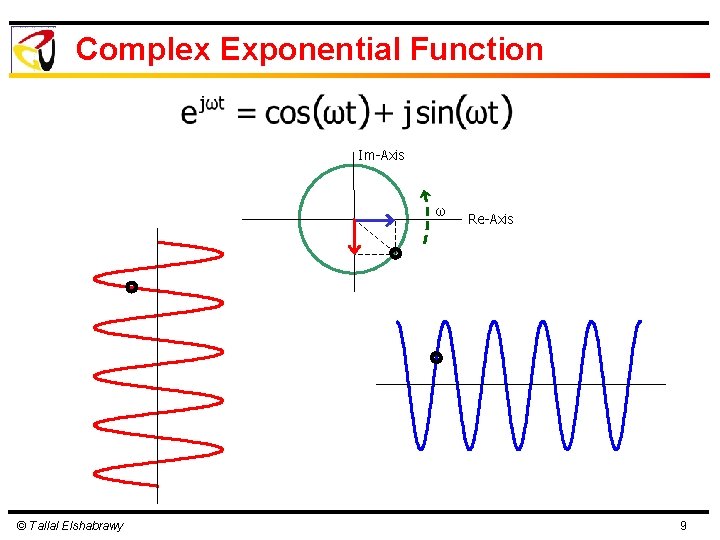
Complex Exponential Function Im-Axis ω © Tallal Elshabrawy Re-Axis 9

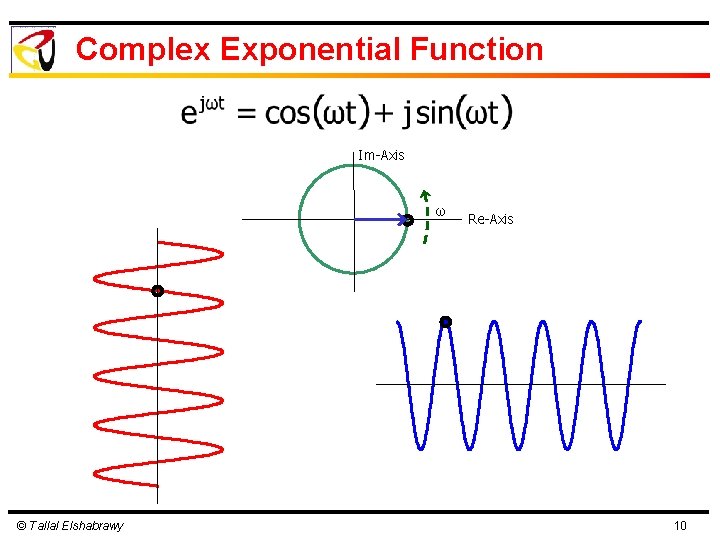
Complex Exponential Function Im-Axis ω © Tallal Elshabrawy Re-Axis 10

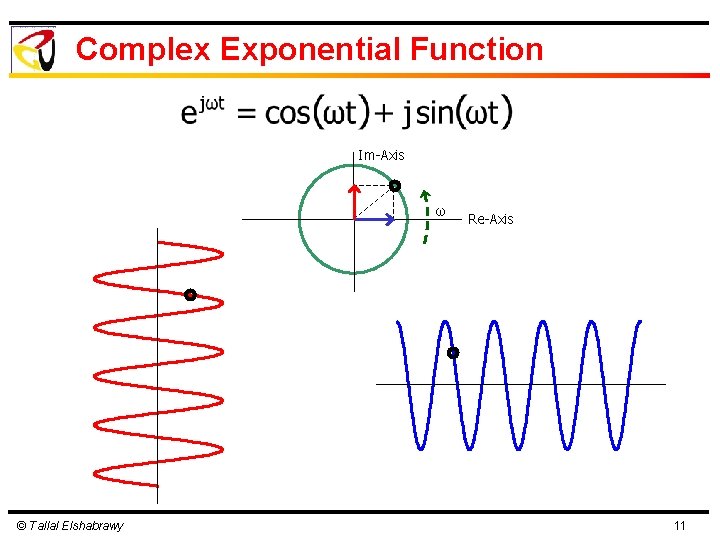
Complex Exponential Function Im-Axis ω © Tallal Elshabrawy Re-Axis 11

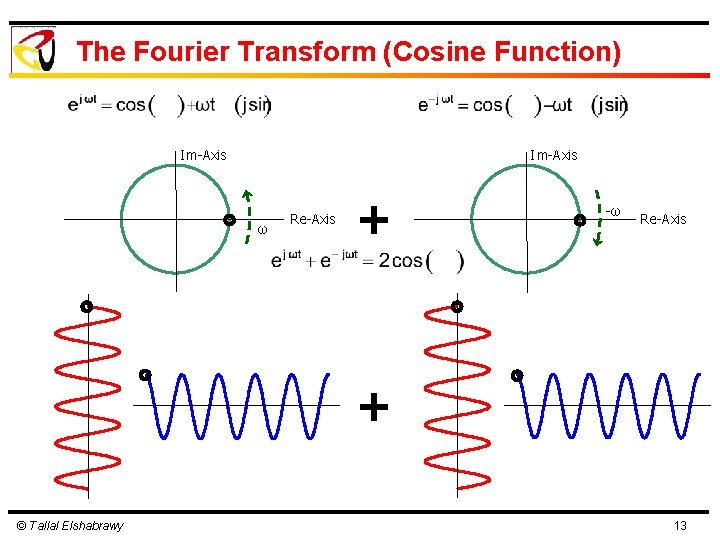
The Fourier Transform Representing functions in terms of complex exponentials with different frequencies © Tallal Elshabrawy 12

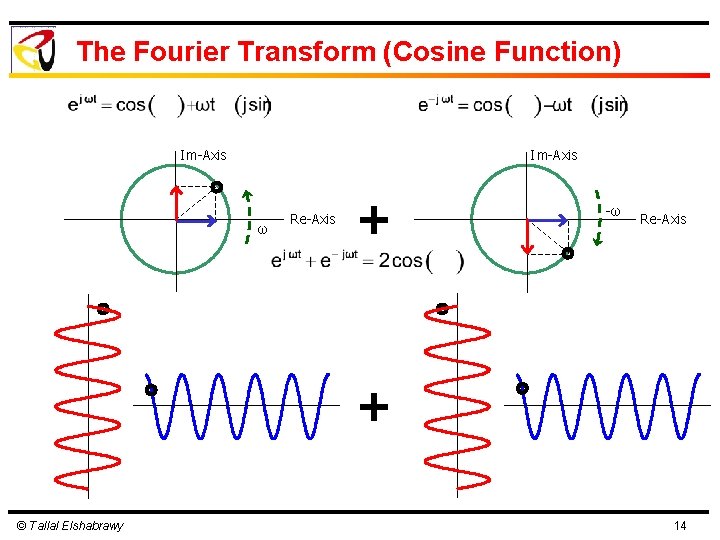
The Fourier Transform (Cosine Function) Im-Axis ω Re-Axis + -ω Re-Axis + © Tallal Elshabrawy 13

The Fourier Transform (Cosine Function) Im-Axis ω Re-Axis + -ω Re-Axis + © Tallal Elshabrawy 14

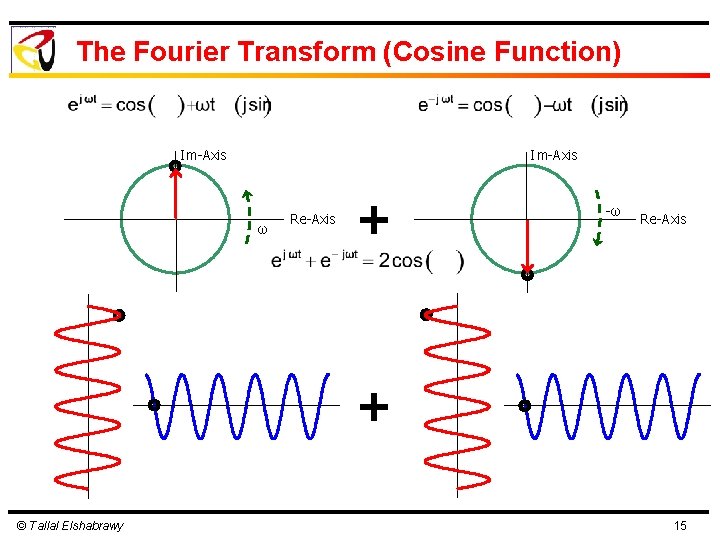
The Fourier Transform (Cosine Function) Im-Axis ω Re-Axis + -ω Re-Axis + © Tallal Elshabrawy 15

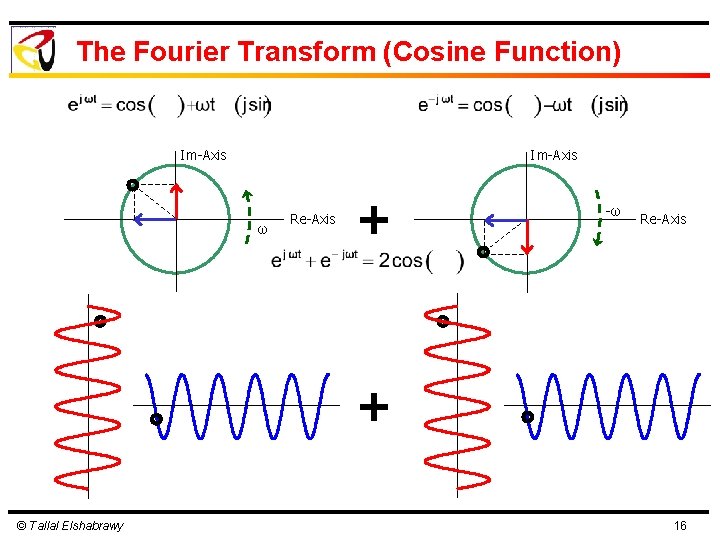
The Fourier Transform (Cosine Function) Im-Axis ω Re-Axis + -ω Re-Axis + © Tallal Elshabrawy 16

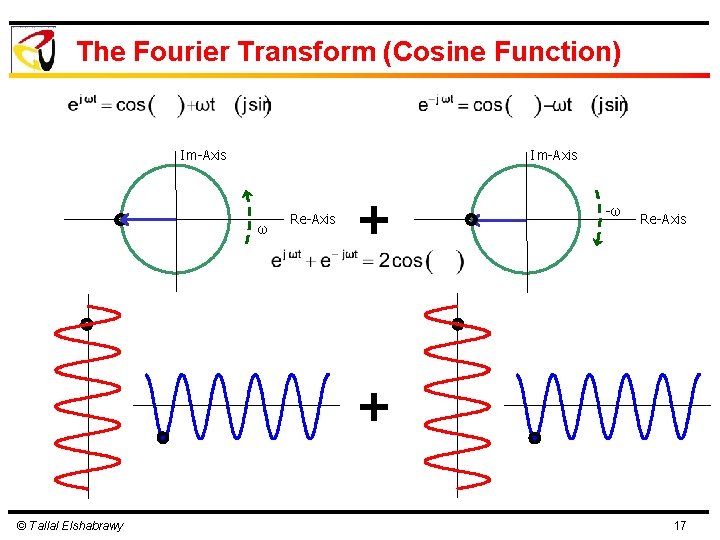
The Fourier Transform (Cosine Function) Im-Axis ω Re-Axis + -ω Re-Axis + © Tallal Elshabrawy 17

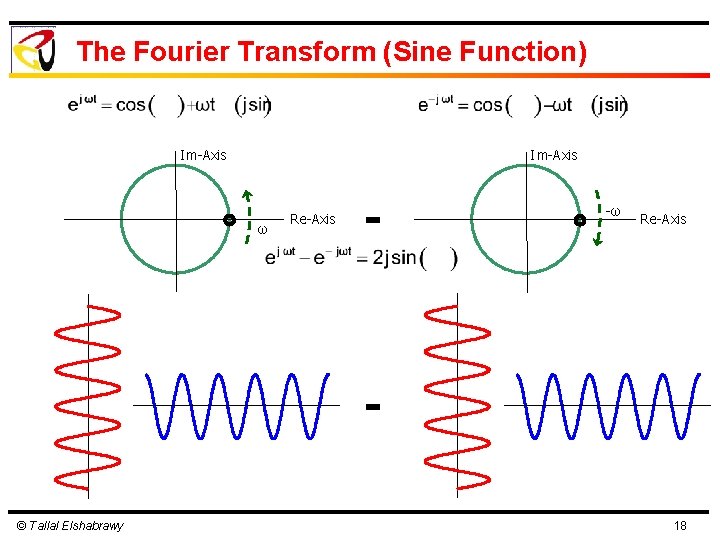
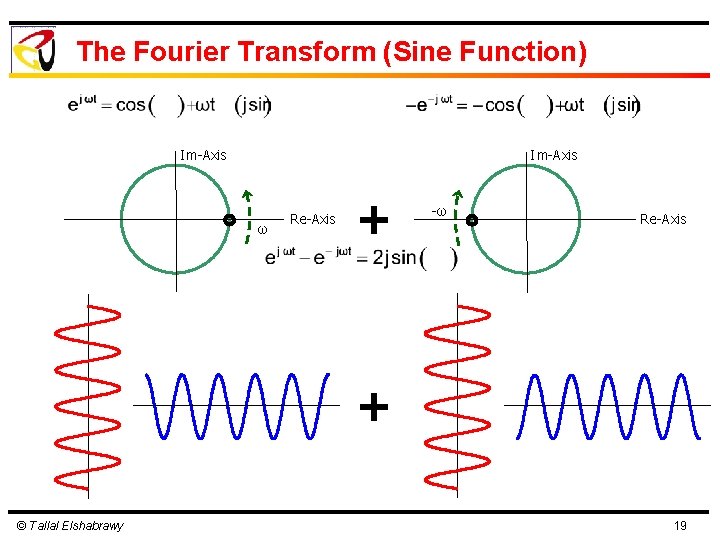
The Fourier Transform (Sine Function) Im-Axis ω Re-Axis - -ω Re-Axis © Tallal Elshabrawy 18

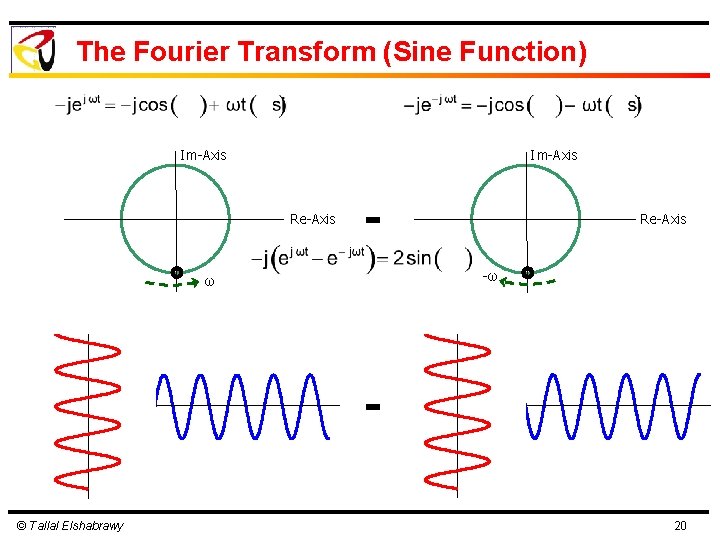
The Fourier Transform (Sine Function) Im-Axis ω Re-Axis + -ω Re-Axis + © Tallal Elshabrawy 19

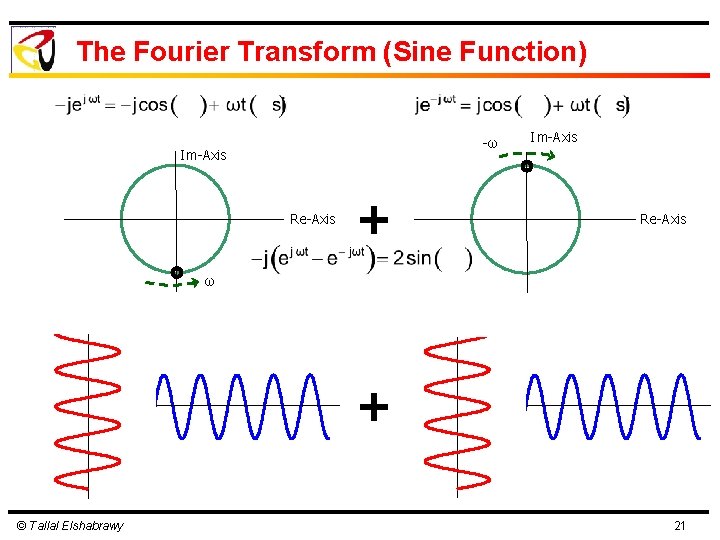
The Fourier Transform (Sine Function) Im-Axis Re-Axis -ω ω © Tallal Elshabrawy 20

The Fourier Transform (Sine Function) -ω Im-Axis Re-Axis + Im-Axis Re-Axis ω + © Tallal Elshabrawy 21

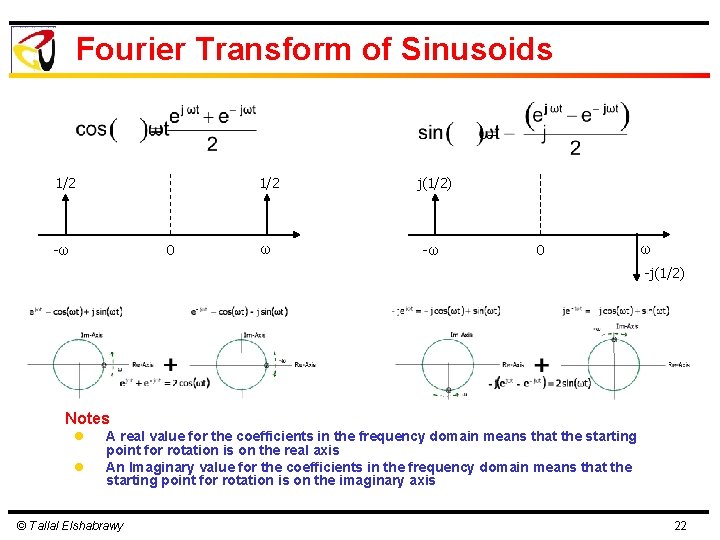
Fourier Transform of Sinusoids 1/2 -ω 0 1/2 j(1/2) ω -ω 0 ω -j(1/2) Notes l l A real value for the coefficients in the frequency domain means that the starting point for rotation is on the real axis An Imaginary value for the coefficients in the frequency domain means that the starting point for rotation is on the imaginary axis © Tallal Elshabrawy 22

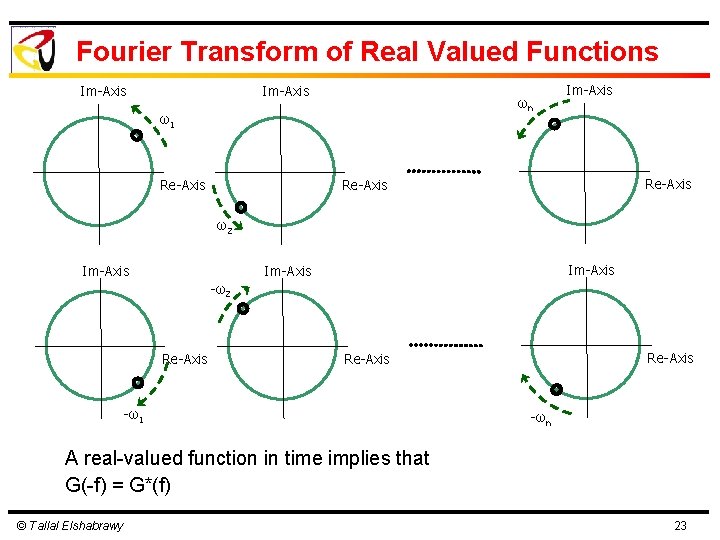
Fourier Transform of Real Valued Functions Im-Axis ωn ω1 Im-Axis Re-Axis ω2 Im-Axis -ω2 Re-Axis -ω1 -ωn A real-valued function in time implies that G(-f) = G*(f) © Tallal Elshabrawy 23
 Iet600
Iet600 Iet electronics letters
Iet electronics letters Complex exponential function graph
Complex exponential function graph Exponential function parent
Exponential function parent Inverse functions logarithmic and exponential
Inverse functions logarithmic and exponential Functions and inverses
Functions and inverses Kingdom archaebacteria (previously monera) cell number
Kingdom archaebacteria (previously monera) cell number Mariam savabi
Mariam savabi Previously approved waivers ncaa
Previously approved waivers ncaa Mse 227 csun
Mse 227 csun Rectangular form complex numbers
Rectangular form complex numbers Real exponential sequence
Real exponential sequence Pauline and bruno have a big argument
Pauline and bruno have a big argument Miliary tb
Miliary tb Simple compound complex quiz
Simple compound complex quiz The electra complex
The electra complex Psychodynamic perspective
Psychodynamic perspective Sublimation in psychology
Sublimation in psychology Constant ratio example
Constant ratio example Exponential functions formula
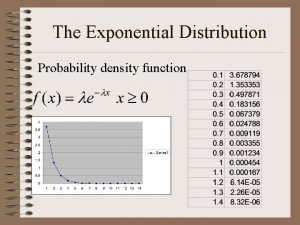
Exponential functions formula Exponential distribution function
Exponential distribution function Exponential table of values
Exponential table of values Decay constant from half life
Decay constant from half life Rational function parent function
Rational function parent function