Huffman Coding The most for the least Design

Huffman Coding The most for the least

Design Goals l l Encode messages parsimoniously No character code can be the prefix for another

Requirements l l Message statistics Data structures to create and store new codes

Conventional Encoding Schemes l Fixed length codes – l l E. g. , Unicode, ASCII, rgb Sample data Optimal code length (in bits) is given by the entropy E: Freq Log 2(Freq) -Product A 0. 13 -2. 9434165 0. 382644 B 0. 27 -1. 8889687 0. 510022 C 0. 35 -1. 5145732 0. 530101 D 0. 17 -2. 5563933 0. 434587 E 0. 08 -3. 6438562 0. 291508 Entropy=> 2. 148862

Huffman Algorithm l While (two or more trees in the Forest) – – Find the two least weight trees i and j Create a code Tree node whose left child is the root of tree i and right child is the root of tree j Join the two least weight trees and replace tree i Delete tree j

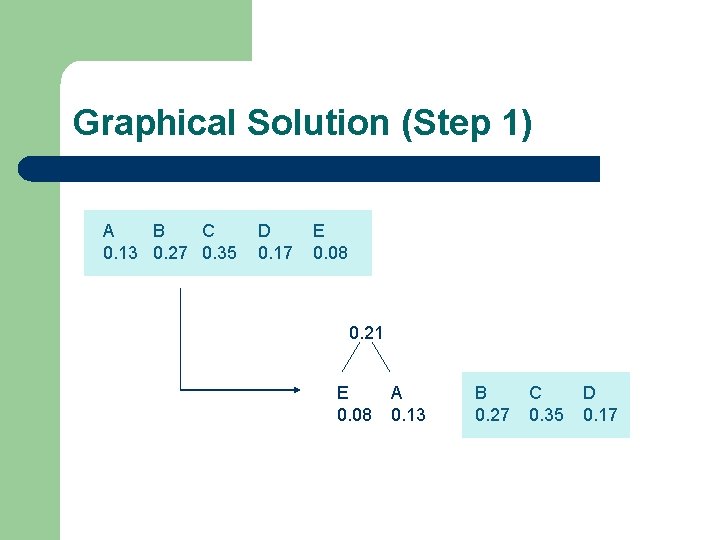
Graphical Solution (Step 1) A B C 0. 13 0. 27 0. 35 D 0. 17 E 0. 08 0. 21 E 0. 08 A 0. 13 B 0. 27 C 0. 35 D 0. 17

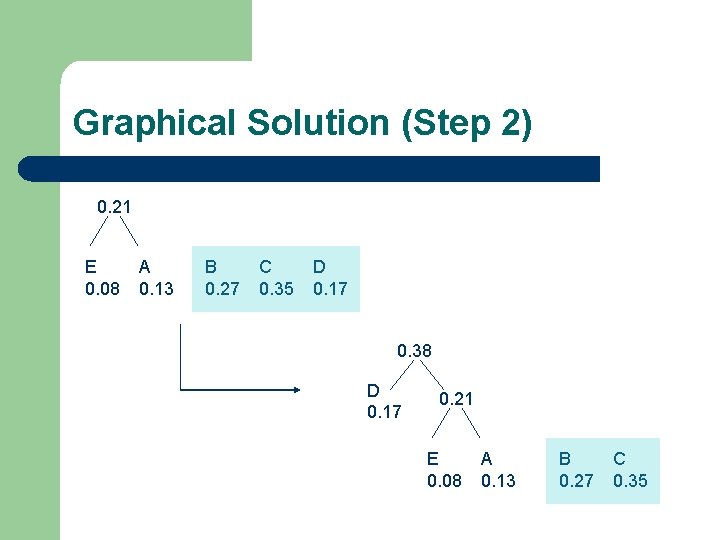
Graphical Solution (Step 2) 0. 21 E 0. 08 A 0. 13 B 0. 27 C 0. 35 D 0. 17 0. 38 D 0. 17 0. 21 E 0. 08 A 0. 13 B 0. 27 C 0. 35

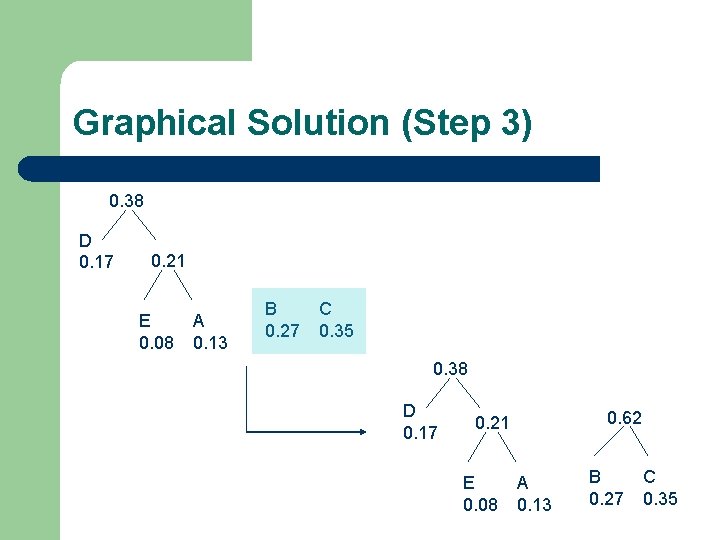
Graphical Solution (Step 3) 0. 38 D 0. 17 0. 21 E 0. 08 A 0. 13 B 0. 27 C 0. 35 0. 38 D 0. 17 0. 62 0. 21 E 0. 08 A 0. 13 B 0. 27 C 0. 35

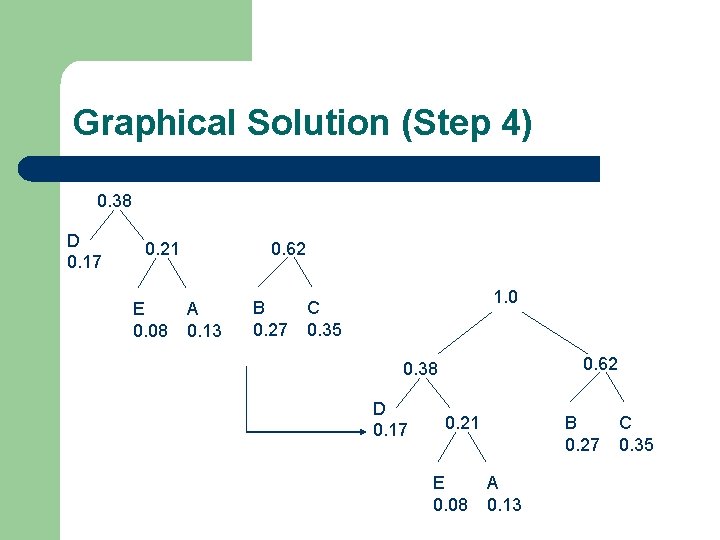
Graphical Solution (Step 4) 0. 38 D 0. 17 0. 62 0. 21 E 0. 08 A 0. 13 B 0. 27 1. 0 C 0. 35 0. 62 0. 38 D 0. 17 B 0. 27 0. 21 E 0. 08 A 0. 13 C 0. 35

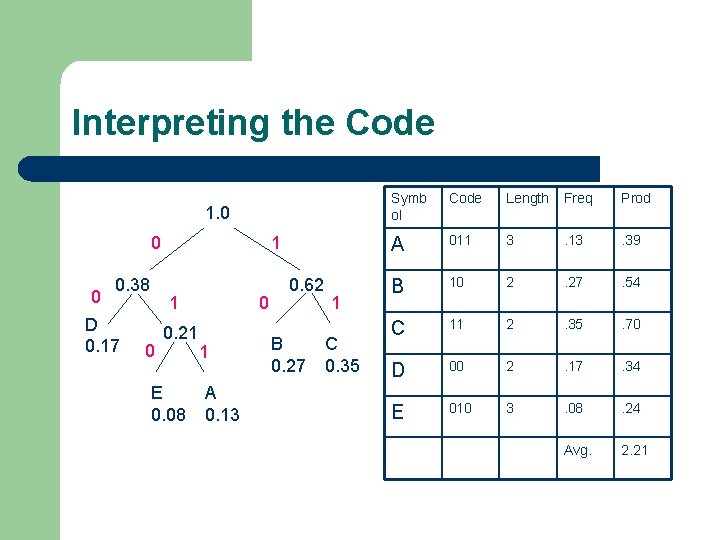
Interpreting the Code 1. 0 0. 38 D 0. 17 1 1 0 0. 21 E 0. 08 0 1 A 0. 13 0. 62 B 0. 27 1 C 0. 35 Symb ol Code Length Freq Prod A 011 3 . 13 . 39 B 10 2 . 27 . 54 C 11 2 . 35 . 70 D 00 2 . 17 . 34 E 010 3 . 08 . 24 Avg. 2. 21

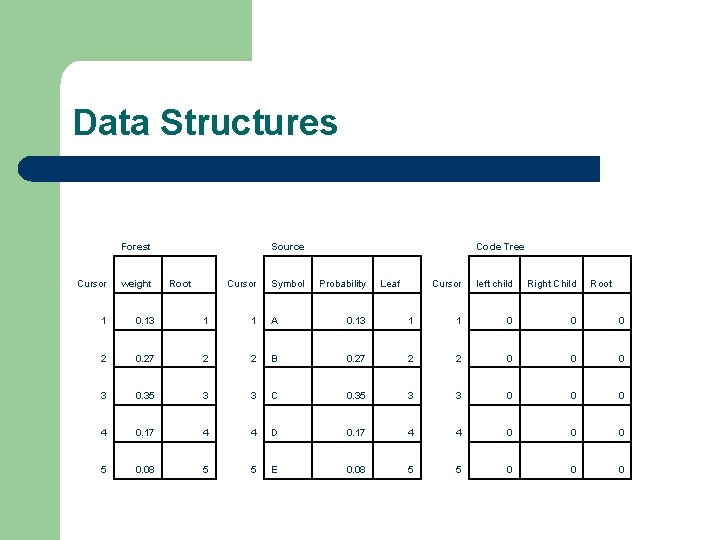
Data Structures Forest Source Root Cursor Symbol Code Tree Cursor weight Probability 1 0. 13 1 1 A 0. 13 2 0. 27 2 2 B 3 0. 35 3 3 4 0. 17 4 5 0. 08 5 Leaf Cursor left child Right Child Root 1 1 0 0. 27 2 2 0 0 0 C 0. 35 3 3 0 0 0 4 D 0. 17 4 4 0 0 0 5 E 0. 08 5 5 0 0 0

Step 1 Forest Source Root Cursor Symbol Code Tree Cursor weight Probability 1 0. 13 1 1 A 0. 13 2 0. 27 2 2 B 3 0. 35 3 3 4 0. 17 4 5 0. 08 5 Leaf Cursor left child Right Child Root 1 1 0 0. 27 2 2 0 0 0 C 0. 35 3 3 0 0 0 4 D 0. 17 4 4 0 0 0 5 E 0. 08 5 5 0 0 0

Step 2 Forest Source Root Cursor Symbol Code Tree Cursor weight Probability 1 0. 21 6 1 A 0. 13 2 0. 27 2 2 B 3 0. 35 3 3 4 0. 17 4 Leaf Cursor left child Right Child Root 1 1 0 0 6 0. 27 2 2 0 0 0 C 0. 35 3 3 0 0 0 4 D 0. 17 4 4 0 0 0 5 E 0. 08 5 5 0 0 6 6 5 1 0

Step 3 Forest Source Root Cursor Symbol Code Tree Cursor weight Probability 1 0. 38 7 1 A 0. 13 2 0. 27 2 2 B 3 0. 35 3 3 Leaf Cursor left child Right Child Root 1 1 0 0 6 0. 27 2 2 0 0 0 C 0. 35 3 3 0 0 0 4 D 0. 17 4 4 0 0 7 5 E 0. 08 5 5 0 0 6 6 5 1 7 7 4 6 0

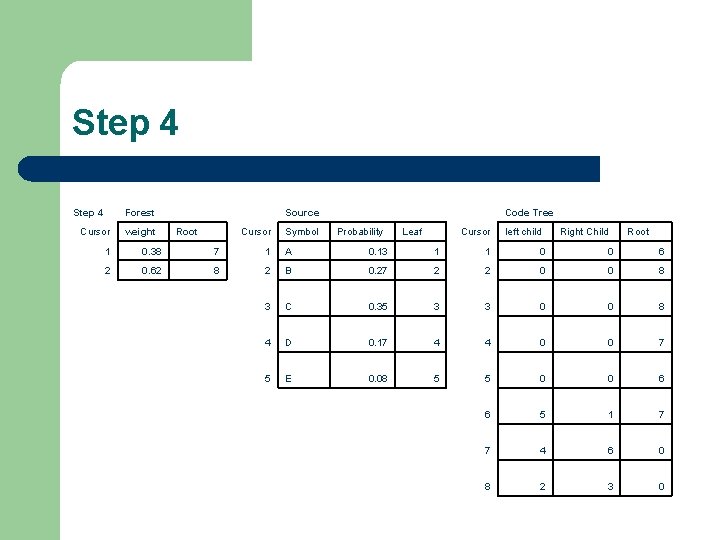
Step 4 Forest Cursor weight Source Root Cursor Symbol Code Tree Probability Leaf Cursor left child Right Child Root 1 0. 38 7 1 A 0. 13 1 1 0 0 6 2 0. 62 8 2 B 0. 27 2 2 0 0 8 3 C 0. 35 3 3 0 0 8 4 D 0. 17 4 4 0 0 7 5 E 0. 08 5 5 0 0 6 6 5 1 7 7 4 6 0 8 2 3 0

Step 5 Forest Cursor 1 Source weight 1 Root Cursor 9 Symbol Code Tree Probability Leaf Cursor left child Right Child Root 1 A 0. 13 1 1 0 0 6 2 B 0. 27 2 2 0 0 8 3 C 0. 35 3 3 0 0 8 4 D 0. 17 4 4 0 0 7 5 E 0. 08 5 5 0 0 6 6 5 1 7 7 4 6 9 8 2 3 9 9 7 8 0