Image Compression CS 474674 Prof Bebis Chapter 8

Image Compression CS 474/674 – Prof. Bebis Chapter 8 (except Sections 8. 10 -8. 12)

Image Compression • The goal of image compression is to reduce the amount of data required to represent a digital image.

Image Compression (cont’d) • Lossless – Information preserving – Low compression ratios • Lossy – Information loss – High compression ratios Trade-off: information loss vs compression ratio

Data ≠ Information • Data and information are not synonymous terms! • Data is the means by which information is conveyed. Goal of data compression Reduce the amount of data while preserving as much information as possible!

Data vs Information (cont’d) • The same information can be represented by different amount of data – for example: Ex 1: Your wife, Helen, will meet you at Logan Airport in Boston at 5 minutes past 6: 00 pm tomorrow night Ex 2: Your wife will meet you at Logan Airport at 5 minutes past 6: 00 pm tomorrow night Ex 3: Helen will meet you at Logan at 6: 00 pm tomorrow night

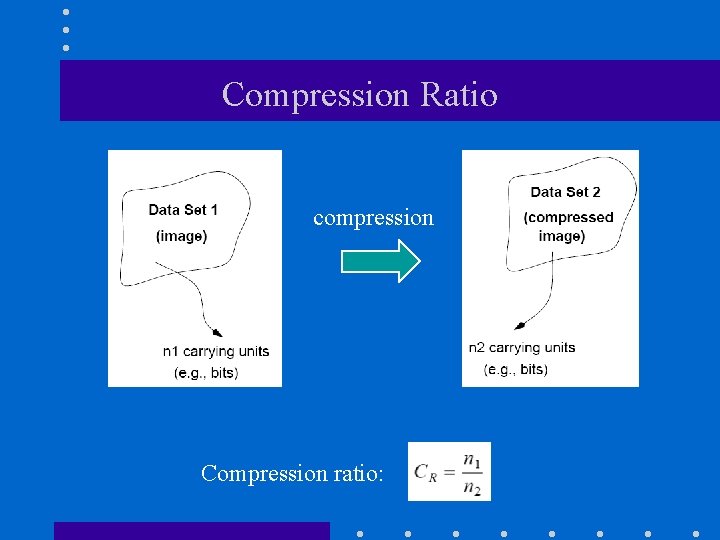
Compression Ratio compression Compression ratio:

Relevant Data Redundancy Example:

Types of Data Redundancy (1) Coding Redundancy (2) Interpixel Redundancy (3) Psychovisual Redundancy • Data compression attempts to reduce one or more of these redundancy types.

Coding Redundancy To reduce coding redundancy, we need efficient coding schemes! • Code: a list of symbols (letters, numbers, bits etc. ) • Code word: a sequence of symbols used to represent some information (e. g. , gray levels). • Code word length: number of symbols in a code word. – Could be fixed or variable

Coding Redundancy (cont’d) • To compare the efficiency of different coding schemes, we need to compute the average number of symbols Lavg per code word. Example: Average Image Size: N x M image rk: k-th gray level l(rk): # of bits for rk P(rk): probability of rk

Coding Redundancy (cont’d) • Case 1: l(rk) = fixed length (code 1) Example:

Coding Redundancy (cont’d) • Case 2: l(rk) = variable length (code 2 – Huffman code) Total number of bits: 2. 7 NM

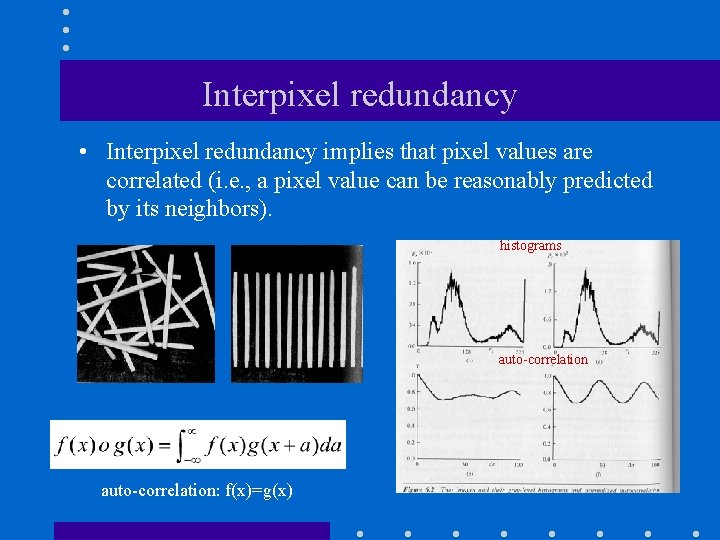
Interpixel redundancy • Interpixel redundancy implies that pixel values are correlated (i. e. , a pixel value can be reasonably predicted by its neighbors). histograms auto-correlation: f(x)=g(x)

Interpixel redundancy (cont’d) • To reduce interpixel redundancy, some kind of a transformation must be applied on the data. Example Original Additional savings using run-length coding threshold 11 …………… 0000…………. . 11…. . 000…. . Binary image (1+10) bits/pair

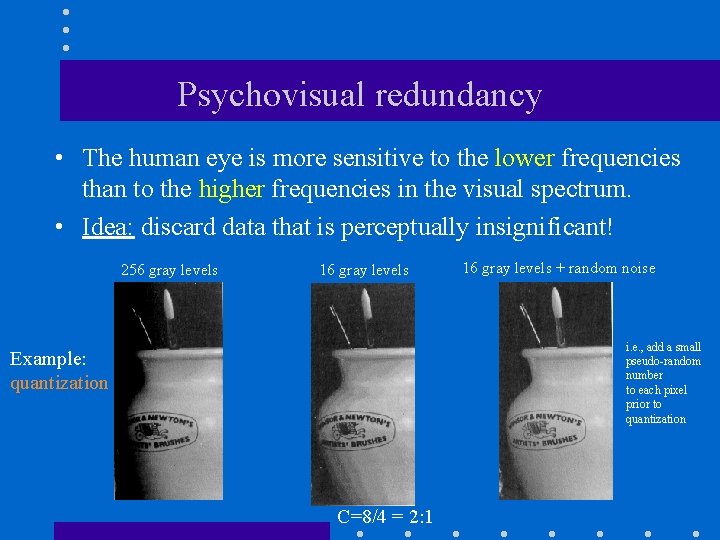
Psychovisual redundancy • The human eye is more sensitive to the lower frequencies than to the higher frequencies in the visual spectrum. • Idea: discard data that is perceptually insignificant! 256 gray levels 16 gray levels + random noise i. e. , add a small pseudo-random number to each pixel prior to quantization Example: quantization C=8/4 = 2: 1

Measuring Information • The key question in image compression is: “What is the minimum amount of data that is sufficient to describe completely an image without loss of information? ” • How do we measure the information content of an image?

Measuring Information (cont’d) • We assume that information generation is a probabilistic process. • Associate information with probability! A random event E with probability P(E) contains: Note: I(E)=0 when P(E)=1

How much information does a pixel value contain? • Suppose that gray level values are generated by a random process, then rk contains: units of information! (assuming statistically independent random events)

How much information does an image contain? • Average information content of an image: using Entropy: units/pixel (e. g. , bits/pixel)

Redundancy • Redundancy: (data vs info) where: Note: if Lavg= H, then R=0 (no redundancy)

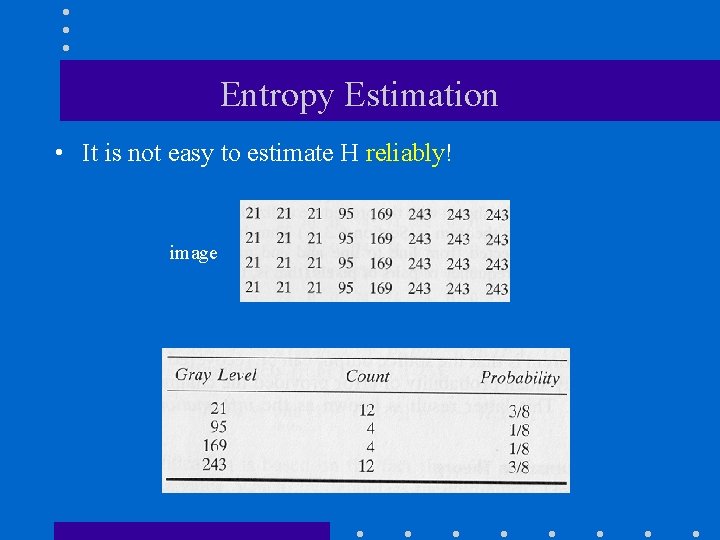
Entropy Estimation • It is not easy to estimate H reliably! image

Entropy Estimation (cont’d) • First order estimate of H: • What is the redundancy? R= Lavg- H where Lavg = 8 bits/pixel R= 6. 19 bits/pixel

Estimating Entropy (cont’d) • Second order estimate of H: – Use relative frequencies of pixel blocks : image

Estimating Entropy (cont’d) • What does it mean that the first- and second-order entropies are different? • In general, differences between first-order and higher-order entropy estimates indicate the presence of interpixel redundancy (i. e. , need to apply some transformation).

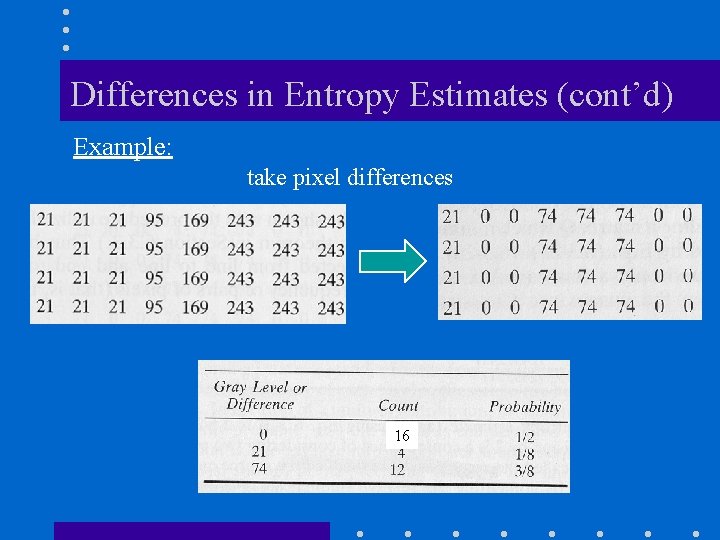
Differences in Entropy Estimates (cont’d) Example: take pixel differences 16

Differences in Entropy Estimates (cont’d) Example (cont’d): – What is the entropy of the pixel differences image? (better than the entropy of the original image H=1. 81) – An even better transformation should be possible since the second order entropy estimate is lower:

Image Compression Model We will focus on the Source Encoder/Decoder only.

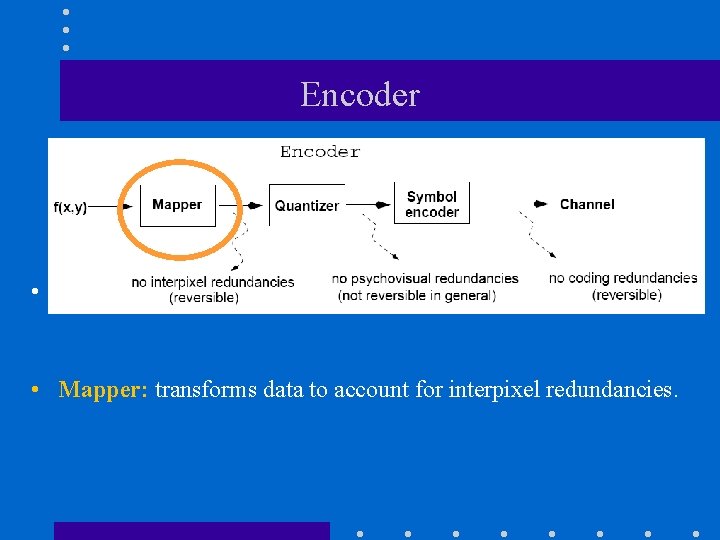
Encoder • • Mapper: transforms data to account for interpixel redundancies.

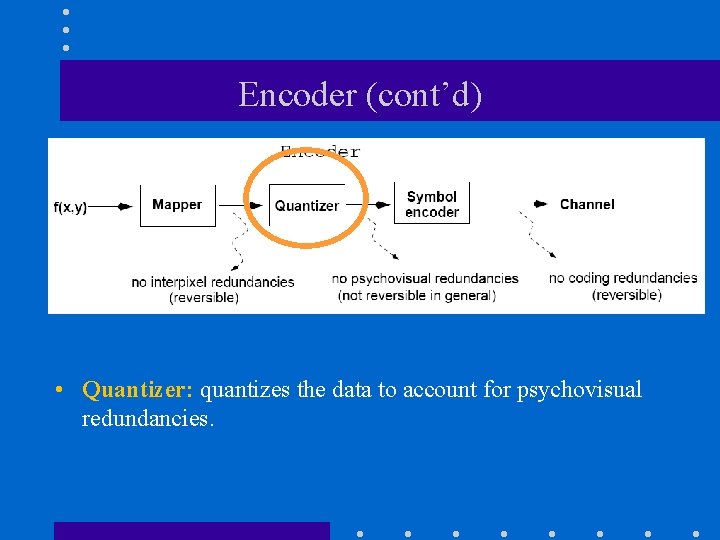
Encoder (cont’d) • • Quantizer: quantizes the data to account for psychovisual redundancies.

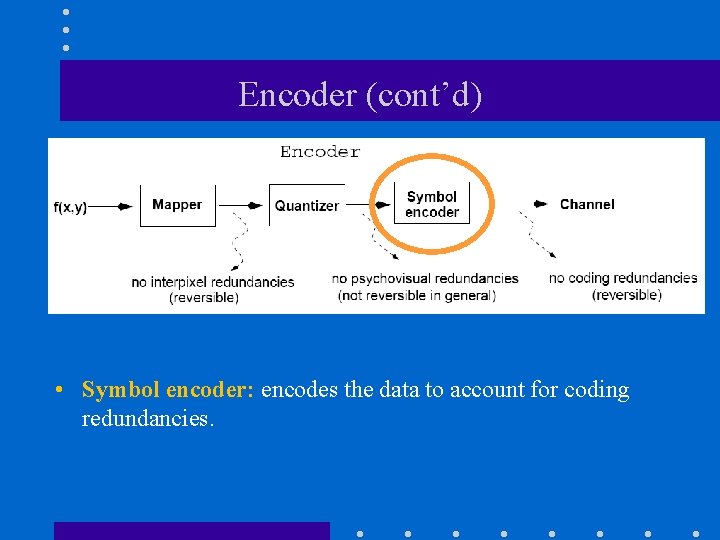
Encoder (cont’d) • • Symbol encoder: encodes the data to account for coding redundancies.

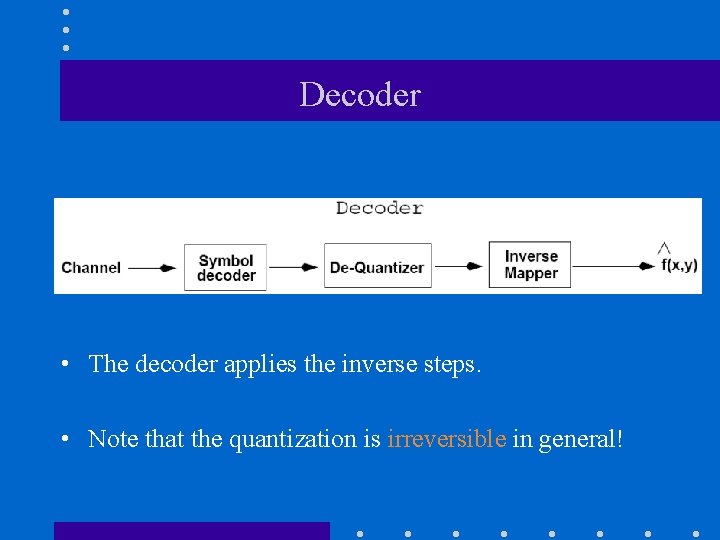
Decoder • The decoder applies the inverse steps. • Note that the quantization is irreversible in general!

Fidelity Criteria • How close is to ? • Criteria – Subjective: based on human observers – Objective: mathematically defined criteria

Subjective Fidelity Criteria

Objective Fidelity Criteria • Root mean square error (RMS) • Mean-square signal-to-noise ratio (SNR)

Lossless Compression

Taxonomy of Lossless Methods (Run-length encoding) (see “Image Compression Techniques” paper)

Huffman Coding (addresses coding redundancy) • A variable-length coding technique. • Source symbols are encoded one at a time! • There is a one-to-one correspondence between source symbols and code words. • Optimal code - minimizes code word length per source symbol.

Huffman Coding (cont’d) • Forward Pass 1. Sort probabilities per symbol 2. Combine the lowest two probabilities 3. Repeat Step 2 until only two probabilities remain.

Huffman Coding (cont’d) • Backward Pass Assign code symbols going backwards

Huffman Coding (cont’d) • Lavg assuming binary coding: • Lavg assuming Huffman coding:

Huffman Coding-Decoding • Both coding and decoding can be implemented using a look-up table. • Note that decoding can be done unambiguously.

Arithmetic (or Range) Coding (addresses coding redundancy) • Huffman coding encodes source symbols one at a time which might not be efficient. • Arithmetic coding encodes sequences of source symbols to variable length code words. – There is no one-to-one correspondence between source symbols and code words. – Slower than Huffman coding but can achieve better compression.

Arithmetic Coding (cont’d) • Main idea: – Map a sequence of symbols to a number (arithmetic code) in the interval [0, 1). – Encoding the arithmetic code is more efficient. α 1 α 2 α 3 α 4 – The mapping depends on the probabilities of the symbols. – The mapping is built as each symbol arrives.

Arithmetic Coding (cont’d) • Main idea: α 1 α 2 α 3 α 4 – Start with the interval [0, 1) 0 1 – A sub-interval of [0, 1) is chosen to represent the first symbol (based on its probability of occurrence). 0 1 – As more symbols are encoded, the sub-interval gets smaller and smaller. 0 1 – At the end, the symbol sequence is encoded by a number within the final interval.

Example Encode α 1 α 2 α 3 α 4 [0. 06752, 0. 0688) code: 0. 068 (any number within sub-interval) 0. 8 0. 4 0. 2 Warning: finite precision arithmetic might cause problems due to truncations!

Example (cont’d) • The arithmetic code 0. 068 can be encoded using Binary Fraction: 0. 0068 ≈ 0. 00011 (9 bits) (subject to conversion error; exact value is 0. 068359375) • Huffman Code: 0100011001 (10 bits) • Fixed Binary Code: 5 x 8 bits/symbol = 40 bits α 1 α 2 α 3 α 4

Arithmetic Decoding 1. 0 0. 8 0. 72 0. 592 0. 5728 0. 72 0. 688 0. 5856 0. 57152 α 4 Decode 0. 572 α 3 0. 4 0. 56 0. 624 0. 5728 0. 56896 α 2 α 3 α 1 α 2 α 4 0. 2 0. 48 0. 592 0. 5664 0. 56768 α 1 0. 0 0. 4 0. 5664

LZW Coding (addresses interpixel redundancy) • Requires no prior knowledge of symbol probabilities. • Assigns sequences of source symbols to fixed length code words. – There is no one-to-one correspondence between source symbols and code words. • Included in GIF, TIFF and PDF file formats

LZW Coding • A codebook (or dictionary) needs to be constructed. • Initially, the first 256 entries of the dictionary are assigned to the gray levels 0, 1, 2, . . , 255 (i. e. , assuming 8 bits/pixel) Initial Dictionary Location Entry 0 1. 255 256 0 1. 255 - 511 -

LZW Coding (cont’d) 39 39 Example: 39 126 126 Dictionary Location As the encoder examines image pixels, gray level sequences (i. e. , blocks) that are not in the dictionary are assigned to a new entry. Entry 0 1. 255 256 0 1. 255 39 -39 511 - - Is 39 in the dictionary……. . Yes - What about 39 -39…………. No * Add 39 -39 at location 256

Example 39 39 126 126 Concatenated Sequence: CS = CR + P (CR) (P) CR = empty repeat P=next pixel CS=CR + P If CS is found: (1) No Output (2) CR=CS else: (1) Output D(CR) (2) Add CS to D (3) CR=P 10 x 9 bits/symbol = 90 bits vs 16 x 8 bits/symbol = 128 bits

Decoding LZW • Decoding can be done using the dictionary again. • No need to transmit the dictionary for decoding; it can be built on the “fly” by the decoder as it reads the received code words.

Run-length coding (RLC) (addresses interpixel redundancy) • Reduce the size of a repeating string of symbols (i. e. , runs): 1 1 1 0 0 0 1 (1, 5) (0, 6) (1, 1) a a a b b b c c (a, 3) (b, 6) (c, 2) • • Encodes a run of symbols into two bytes: (symbol, count) Can compress any type of data but cannot achieve high compression ratios compared to other compression methods.

Combining Huffman Coding with Run-length Coding • Assuming that a message has been encoded using Huffman coding, additional compression can be achieved using run-length coding. e. g. , (0, 1)(1, 1)(0, 1)(1, 0)(0, 2)(1, 4)(0, 2)

Bit-plane coding (addresses interpixel redundancy) • Process each bit plane individually. (1) Decompose an image into a series of binary images. (2) Compress each binary image (e. g. , using run-length coding)

Lossy Methods - Taxonomy (see “Image Compression Techniques” paper)

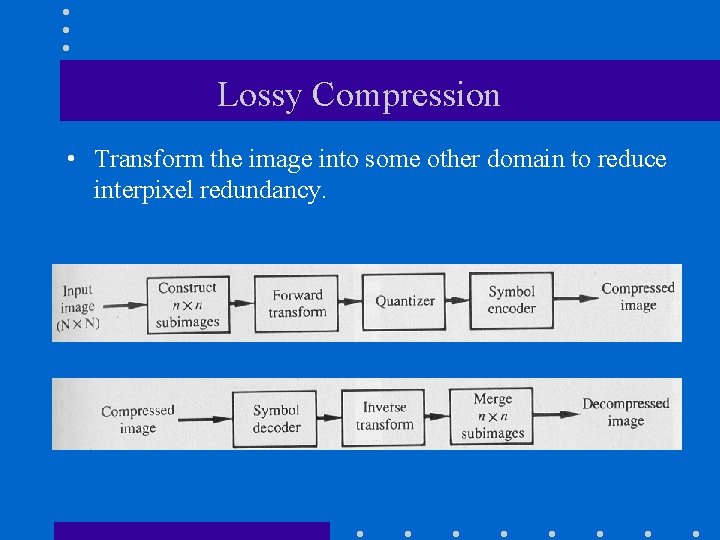
Lossy Compression • Transform the image into some other domain to reduce interpixel redundancy.

Example: Fourier Transform Note that the magnitude of the FT decreases, as u, v increase! K << N K-1

Transform Selection • T(u, v) can be computed using various transformations, for example: – DFT – DCT (Discrete Cosine Transform) – KLT (Karhunen-Loeve Transformation) or Principal Component Analysis (PCA) • JPEG uses DCT for handling interpixel redundancy.

DCT (Discrete Cosine Transform) Forward: Inverse: if u=0 if u>0 if v=0 if v>0

DCT (cont’d) • Basis functions for a 4 x 4 image (i. e. , cosines of different frequencies).

DCT (cont’d) DFT WHT DCT Using 8 x 8 sub-images yields 64 coefficients per sub-image. Reconstructed images by truncating 50% of the coefficients DCT is a more compact transformation! RMS error: 2. 32 1. 78 1. 13

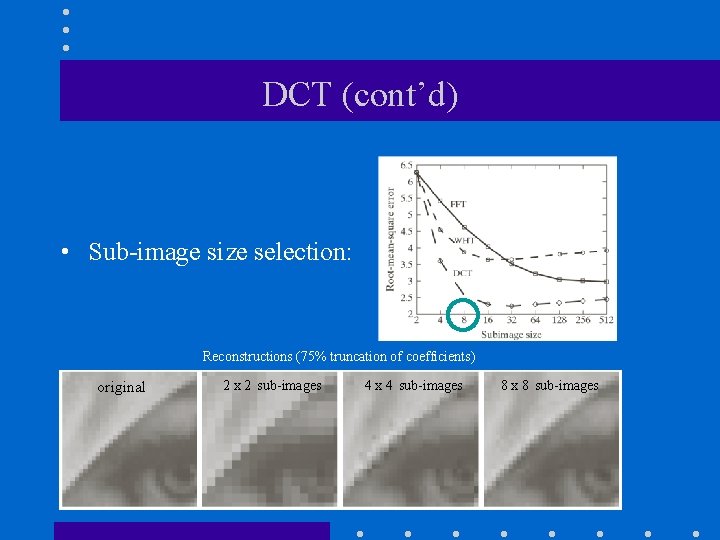
DCT (cont’d) • Sub-image size selection: Reconstructions (75% truncation of coefficients) original 2 x 2 sub-images 4 x 4 sub-images 8 x 8 sub-images

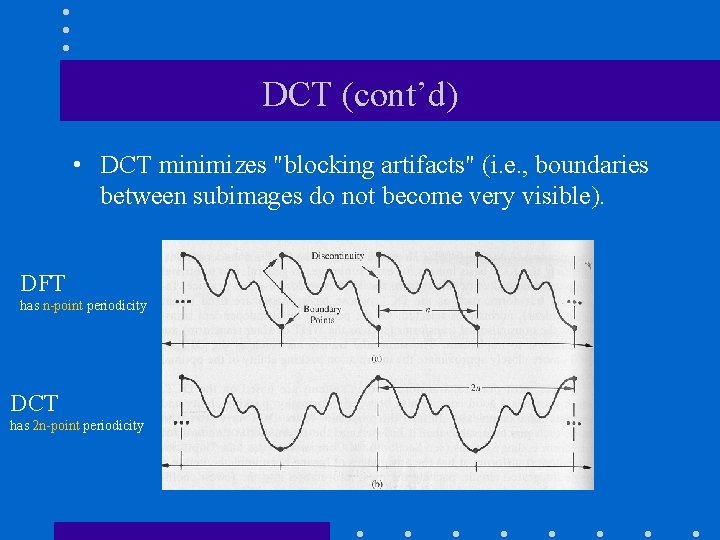
DCT (cont’d) • DCT minimizes "blocking artifacts" (i. e. , boundaries between subimages do not become very visible). DFT has n-point periodicity DCT has 2 n-point periodicity

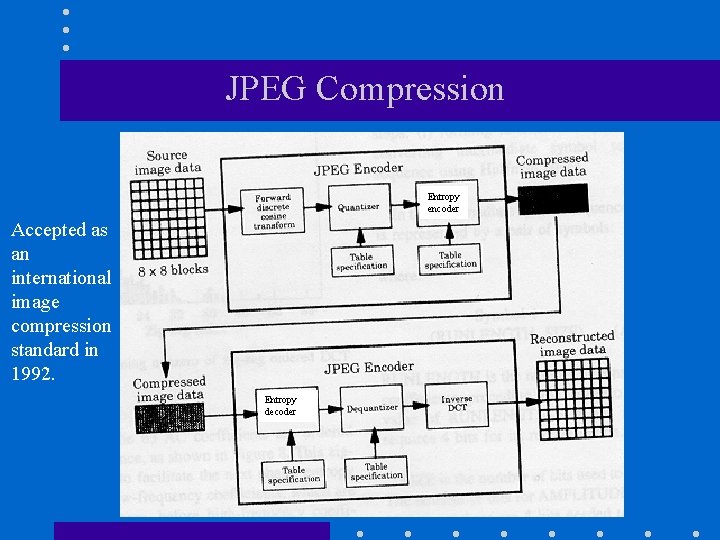
JPEG Compression Entropy encoder Accepted as an international image compression standard in 1992. Entropy decoder

JPEG - Steps 1. Divide image into 8 x 8 subimages. For each subimage do: 2. Shift the gray-levels in the range [-128, 127] 3. Apply DCT 64 coefficients 1 DC coefficient: F(0, 0) 63 AC coefficients: F(u, v)

Example [-128, 127] (DCT spectrum) The low frequency components are around the upper-left corner of the spectrum.

JPEG Steps 4. Quantize the coefficients (i. e. , reduce the amplitude of coefficients that do not contribute a lot). Q(u, v): quantization table

Example • Quantization Table Q[i][j]

Example (cont’d) Quantization

JPEG Steps (cont’d) 5. Order the coefficients using zig-zag ordering - Creates long runs of zeros (i. e. , ideal for run-length encoding)

JPEG Steps (cont’d) 6. Encode coefficients: 6. 1 Form “intermediate” symbol sequence. 6. 2 Encode “intermediate” symbol sequence into a binary sequence. Note: DC coefficient is encoded differently from AC coefficients

Intermediate Symbol Sequence – DC coeff symbol_1 (SIZE) (6) SIZE: # bits need to encode the coefficient symbol_2 (AMPLITUDE) (61)

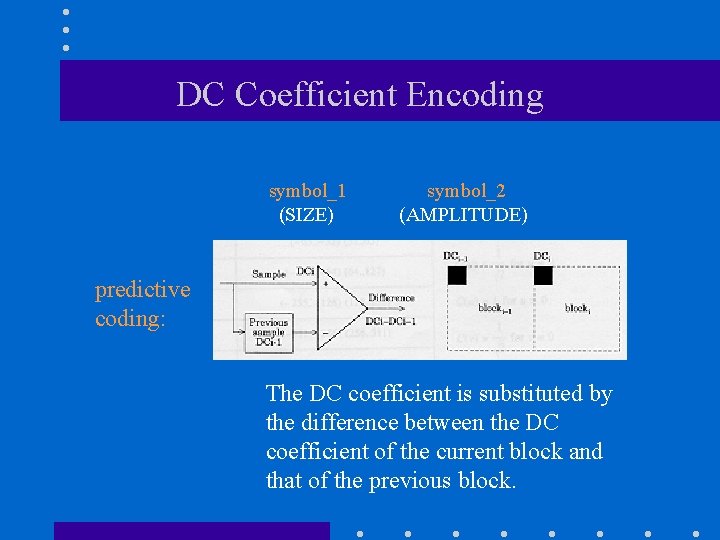
DC Coefficient Encoding symbol_1 (SIZE) symbol_2 (AMPLITUDE) predictive coding: The DC coefficient is substituted by the difference between the DC coefficient of the current block and that of the previous block.

Intermediate Symbol Sequence – AC coeff symbol_1 (RUN-LENGTH, SIZE) symbol_2 (AMPLITUDE) end of block RUN-LENGTH: run of zeros preceding coefficient SIZE: # bits for encoding the amplitude of coefficient Note: If RUN-LENGTH > 15, use symbol (15, 0) ,

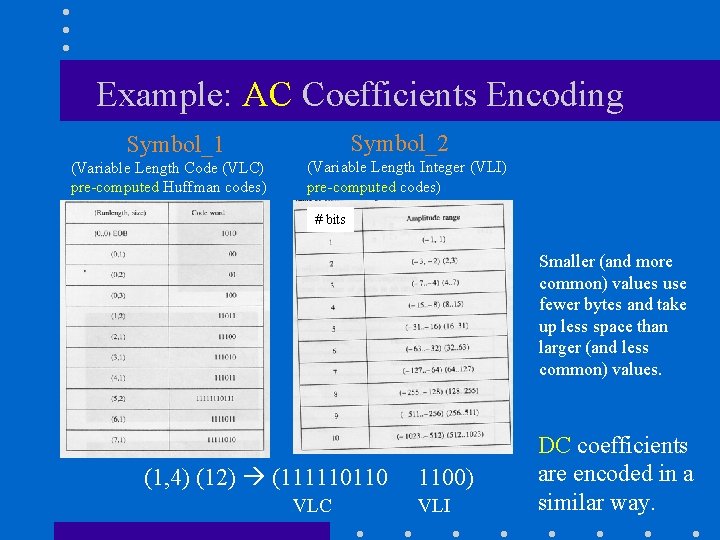
Example: AC Coefficients Encoding Symbol_2 Symbol_1 (Variable Length Code (VLC) pre-computed Huffman codes) (Variable Length Integer (VLI) pre-computed codes) # bits Smaller (and more common) values use fewer bytes and take up less space than larger (and less common) values. (1, 4) (12) (111110110 VLC 1100) VLI DC coefficients are encoded in a similar way.

Final Symbol Sequence

What is the effect of the “Quality” parameter? (58 k bytes) lower compression (21 k bytes) (8 k bytes) higher compression

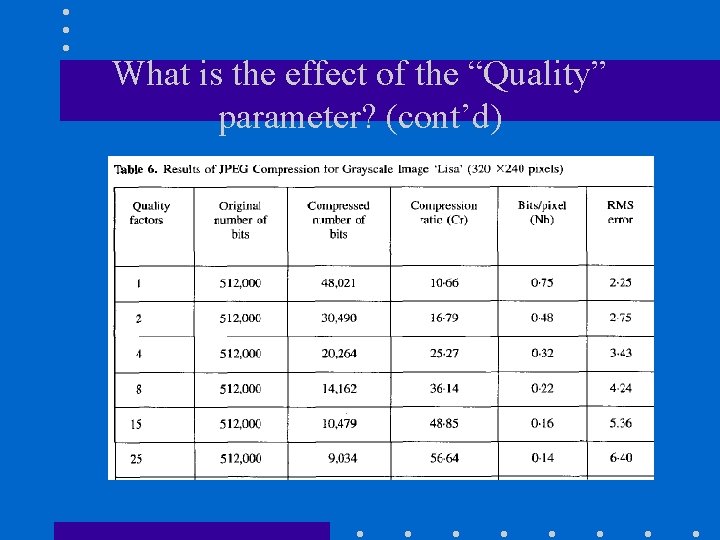
What is the effect of the “Quality” parameter? (cont’d)

Effect of Quantization: homogeneous 8 x 8 block

Effect of Quantization: homogeneous 8 x 8 block (cont’d) Quantized coeff De-quantized coeff

Effect of Quantization: homogeneous 8 x 8 block (cont’d) Reconstructed Error is low! Original

Effect of Quantization: non-homogeneous 8 x 8 block

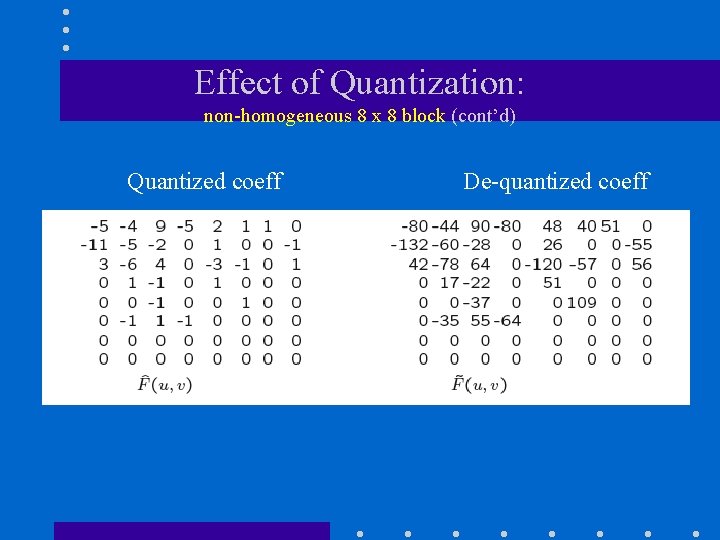
Effect of Quantization: non-homogeneous 8 x 8 block (cont’d) Quantized coeff De-quantized coeff

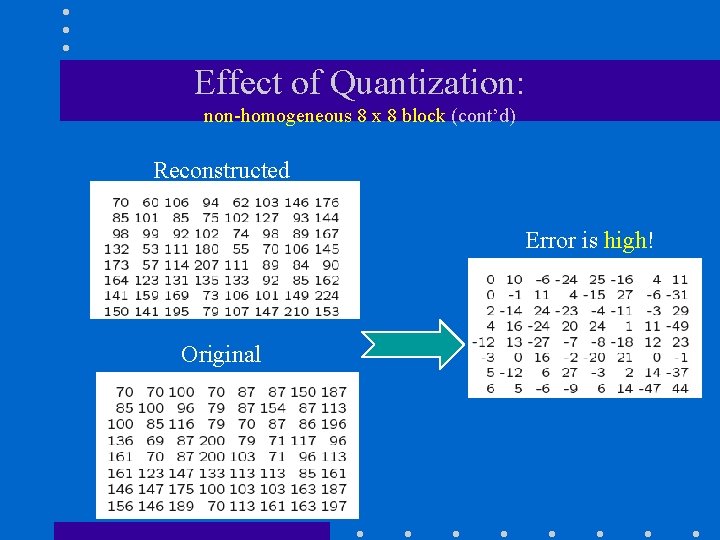
Effect of Quantization: non-homogeneous 8 x 8 block (cont’d) Reconstructed Error is high! Original

Case Study: Fingerprint Compression • FBI is digitizing fingerprints at 500 dots per inch with 8 bits of grayscale resolution. • A single fingerprint card turns into about 10 MB of data! A sample fingerprint image 768 x 768 pixels =589, 824 bytes

WSQ Fingerprint Compression • An image coding standard for digitized fingerprints employing the Discrete Wavelet Transform (Wavelet/Scalar Quantization or WSQ). • Developed and maintained by: – FBI – Los Alamos National Lab (LANL) – National Institute for Standards and Technology (NIST)

Need to Preserve Fingerprint Details The "white" spots in the middle of the black ridges are sweat pores and they are admissible points of identification in court. These details are just a couple pixels wide!

What compression scheme should be used? • Lossless or lossy compression? • In practice lossless compression methods haven’t done better than 2: 1 on fingerprints! • Does JPEG work well for fingerprint compression?

Results using JPEG compression file size 45853 bytes compression ratio: 12. 9 Fine details have been lost. Image has an artificial ‘‘blocky’’ pattern superimposed on it. Artifacts will affect the performance of fingerprint recognition.

Results using WSQ compression file size 45621 bytes compression ratio: 12. 9 Fine details are better preserved. No “blocky” artifacts.

WSQ Algorithm Target bit rate can set via a parameter, similar to the "quality" parameter in JPEG.

Compression ratio • FBI’s target bit rate is around 0. 75 bits per pixel (bpp) • This corresponds to a compression ratio of 8/0. 75=10. 7 • Let’s compare WSQ with JPEG …

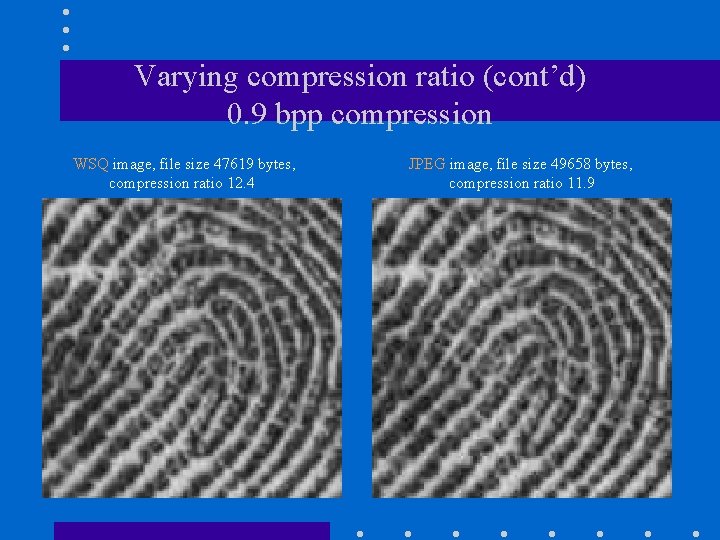
Varying compression ratio (cont’d) 0. 9 bpp compression WSQ image, file size 47619 bytes, compression ratio 12. 4 JPEG image, file size 49658 bytes, compression ratio 11. 9

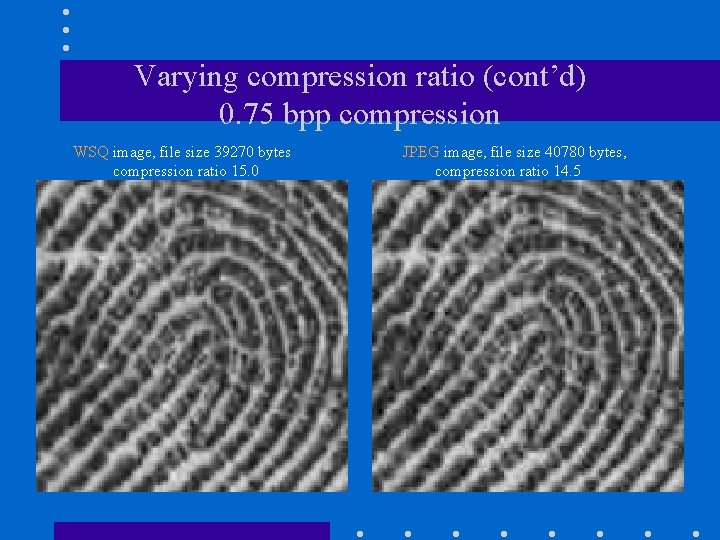
Varying compression ratio (cont’d) 0. 75 bpp compression WSQ image, file size 39270 bytes compression ratio 15. 0 JPEG image, file size 40780 bytes, compression ratio 14. 5

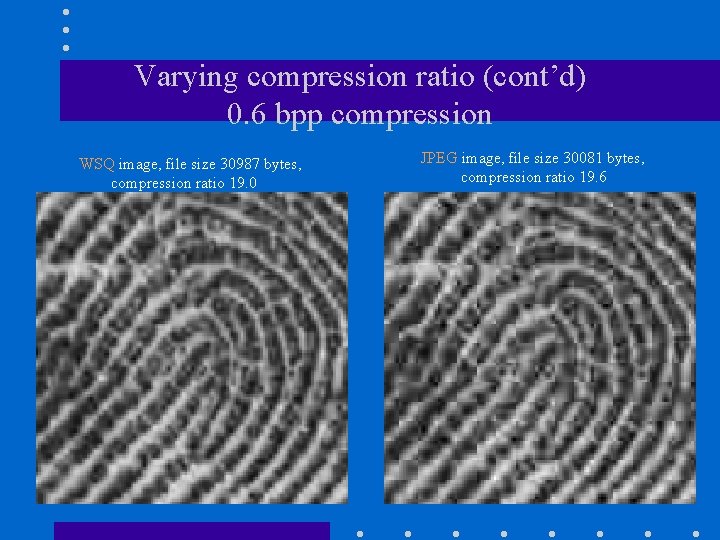
Varying compression ratio (cont’d) 0. 6 bpp compression WSQ image, file size 30987 bytes, compression ratio 19. 0 JPEG image, file size 30081 bytes, compression ratio 19. 6

JPEG Modes • JPEG supports several different modes – – Sequential Mode Progressive Mode Hierarchical Mode Lossless Mode • The default mode is “sequential” – Image is encoded in a single scan (left-to-right, top-tobottom). (see “Survey” paper)

Progressive JPEG • Image is encoded in multiple scans. • Produce a quick, roughly decoded image when transmission time is long. Sequential Progressive

Progressive JPEG (cont’d) • We’ll examine the following algorithms: (1) Progressive spectral selection algorithm (2) Progressive successive approximation algorithm (3) Hybrid progressive algorithm

Progressive JPEG (cont’d) (1) Progressive spectral selection algorithm – Group DCT coefficients into several spectral bands – Send low-frequency DCT coefficients first – Send higher-frequency DCT coefficients next

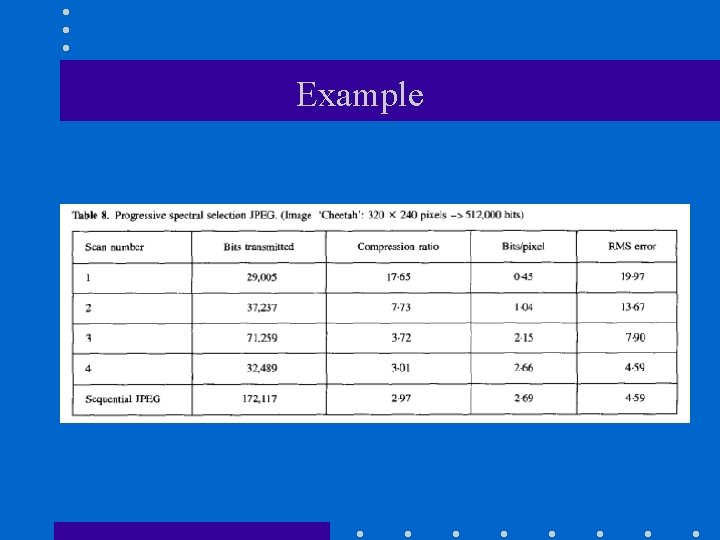
Example

Progressive JPEG (cont’d) (2) Progressive successive approximation algorithm – Send all DCT coefficients but with lower precision. – Refine DCT coefficients in later scans.

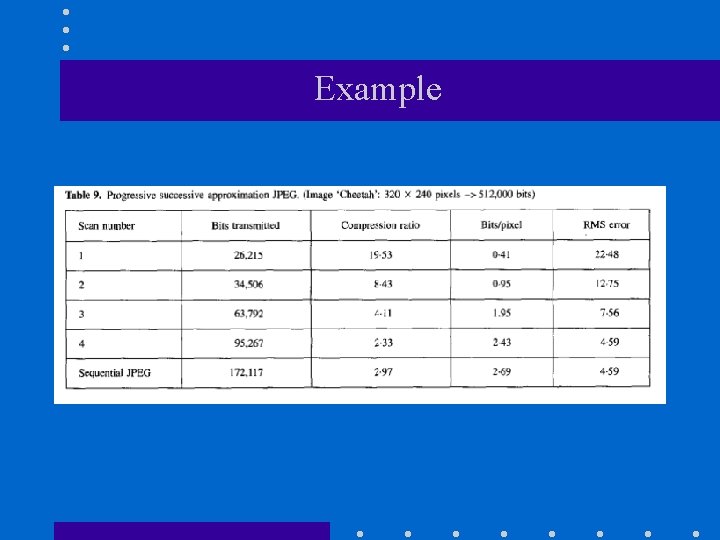
Example

Example after 0. 9 s after 3. 6 s after 1. 6 s after 7. 0 s

Progressive JPEG (cont’d) (3) Combined progressive algorithm – Combines spectral selection and successive approximation.

Hierarchical JPEG • Hierarchical mode encodes the image at different resolutions. • Image is transmitted in multiple passes with increased resolution at each pass.

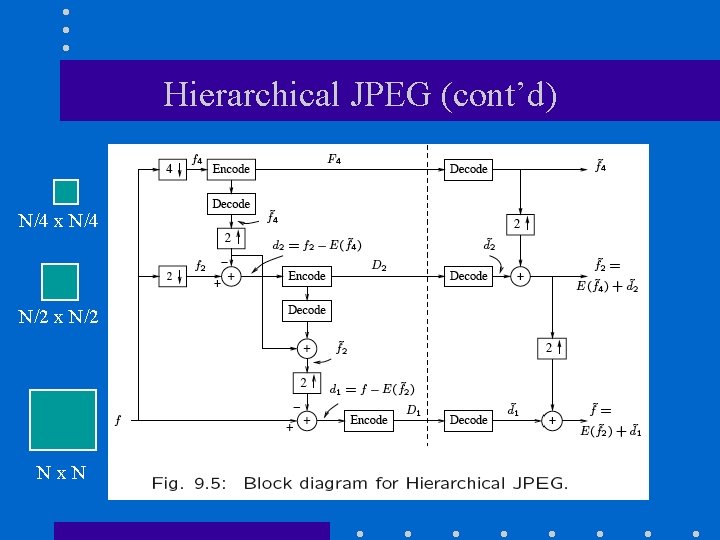
Hierarchical JPEG (cont’d) N/4 x N/4 N/2 x N/2 Nx. N