HighPerformance Grid Computing and Research Networking Algorithms on

High-Performance Grid Computing and Research Networking Algorithms on a Grid of Processors Presented by Xing Hang Instructor: S. Masoud Sadjadi http: //www. cs. fiu. edu/~sadjadi/Teaching/ sadjadi At cs Dot fiu Dot edu

Acknowledgements n The content of many of the slides in this lecture notes have been adopted from the online resources prepared previously by the people listed below. Many thanks! n Henri Casanova n n n Principles of High Performance Computing http: //navet. ics. hawaii. edu/~casanova henric@hawaii. edu 2

2 -D Torus topology n We’ve looked at a ring, but for some applications it’s convenient to look at a 2 -D grid topology √p √p n n A 2 -D grid with “wrap-around” is called a 2 -D torus. Advanced parallel linear algebra libraries/languages allow to combine arbitrary data distribution strategies with arbitrary topologies (Sca. LAPACK, HPF) n n n 1 -D block to a ring 2 -D block to a 2 -D grid cyclic or non-cyclic (more on this later) We can go through all the algorithms we saw on a ring and make them work on a grid In practice, for many linear algebra kernel, using a 2 -D block-cyclic on a 2 D grid seems to work best in most situations n n we’ve seen that blocks are good for locality we’ve seen that cyclic is good for load-balancing 3

Semantics of a parallel linear algebra routine? n Centralized n when calling a function (e. g. , LU) n n n More natural/easy for the user Allows for the library to make data distribution decisions transparently to the user Prohibitively expensive if one does sequences of operations n n and one almost always does so Distributed n when calling a function (e. g. , LU) n n n Assume that the input is already distributed Leave the output distributed May lead to having to “redistributed” data in between calls so that distributions match, which is harder for the user and may be costly as well n n the input data is available on a single “master” machine the input data must then be distributed among workers the output data must be undistributed and returned to the “master” machine For instance one may want to change the block size between calls, or go from a noncyclic to a cyclic distribution Most current software adopt distributed n n more work for the user more flexibility and control 4

Matrix-matrix multiply n n Many people have thought of doing a matrix-multiply on a 2 -D torus Assume that we have three matrices A, B, and C, of size Nx. N Assume that we have p processors, so that p=q 2 is a perfect square and our processor grid is qxq We’re looking at a 2 -D block distribution, but not cyclic n again, that would obfuscate the code too much C 00 C 01 C 02 C 03 A 00 A 01 A 02 A 03 B 00 B 01 B 02 B 03 C 10 C 11 C 12 C 13 A 10 A 11 A 12 A 13 B 10 B 11 B 12 B 13 C 20 C 21 C 22 C 23 A 20 A 21 A 22 A 23 B 20 B 21 B 22 B 23 C 30 C 31 C 32 C 33 A 30 A 31 A 32 A 33 B 30 B 31 B 32 B 33 n We’re going to look at three “classic” algorithms: Cannon, Fox, Snyder 5

Cannon’s Algorithm (1969) n n Very simple (from systolic arrays) Starts with a data redistribution for matrices A and B n n goal is to have only neighbor-to-neighbor communications A is circularly shifted/rotated “horizontally” so that its diagonal is on the first column of processors B is circularly shifted/rotated “vertically” so that its diagonal is on the first row of processors Called preskewing C 00 C 01 C 02 C 03 A 00 A 01 A 02 A 03 B 00 B 11 B 22 B 33 C 10 C 11 C 12 C 13 A 11 A 12 A 13 A 10 B 21 B 32 B 03 C 20 C 21 C 22 C 23 A 22 A 23 A 20 A 21 B 20 B 31 B 02 B 13 C 30 C 31 C 32 C 33 A 30 A 31 A 32 B 30 B 01 B 12 B 23 6

Cannon’s Algorithm Preskewing of A and B For k = 1 to q in parallel Local C = C + A*B Vertical shift of B Horizontal shift of A Postskewing of A and B n Of course, computation and communication could be done in an overlapped fashion locally at each processor 7

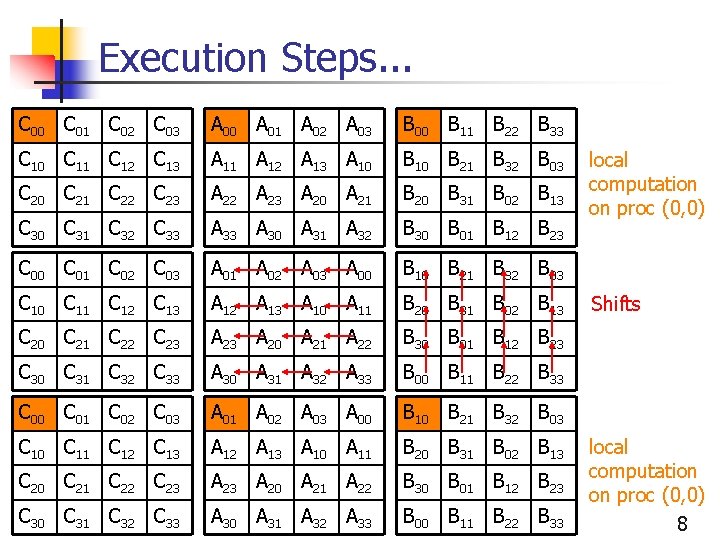
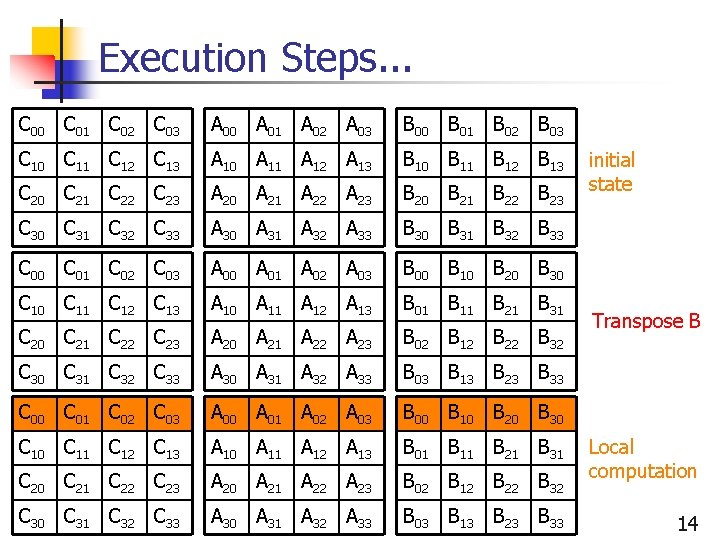
Execution Steps. . . C 00 C 01 C 02 C 03 A 00 A 01 A 02 A 03 B 00 B 11 B 22 B 33 C 10 C 11 C 12 C 13 A 11 A 12 A 13 A 10 B 21 B 32 B 03 C 20 C 21 C 22 C 23 A 22 A 23 A 20 A 21 B 20 B 31 B 02 B 13 C 30 C 31 C 32 C 33 A 30 A 31 A 32 B 30 B 01 B 12 B 23 C 00 C 01 C 02 C 03 A 01 A 02 A 03 A 00 B 10 B 21 B 32 B 03 C 10 C 11 C 12 C 13 A 12 A 13 A 10 A 11 B 20 B 31 B 02 B 13 C 20 C 21 C 22 C 23 A 20 A 21 A 22 B 30 B 01 B 12 B 23 C 30 C 31 C 32 C 33 A 30 A 31 A 32 A 33 B 00 B 11 B 22 B 33 local computation on proc (0, 0) Shifts local computation on proc (0, 0) 8

Fox’s Algorithm(1987) n n Originally developed for Cal. Tech’s Hypercube Uses broadcasts and is also called broadcastmultiply-roll algorithm n broadcasts diagonals of matrix A first diagonal second diagonal third diagonal. . . n n Uses a shift of matrix B No preskewing step 9

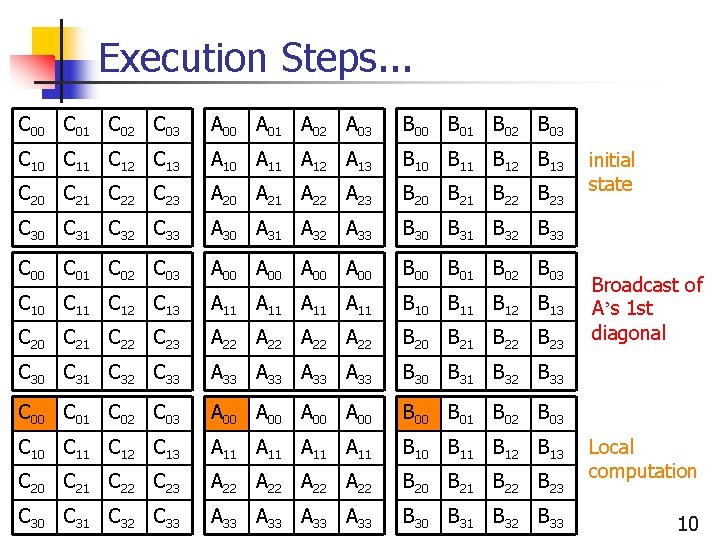
Execution Steps. . . C 00 C 01 C 02 C 03 A 00 A 01 A 02 A 03 B 00 B 01 B 02 B 03 C 10 C 11 C 12 C 13 A 10 A 11 A 12 A 13 B 10 B 11 B 12 B 13 C 20 C 21 C 22 C 23 A 20 A 21 A 22 A 23 B 20 B 21 B 22 B 23 C 30 C 31 C 32 C 33 A 30 A 31 A 32 A 33 B 30 B 31 B 32 B 33 C 00 C 01 C 02 C 03 A 00 A 00 B 00 B 01 B 02 B 03 C 10 C 11 C 12 C 13 A 11 A 11 B 10 B 11 B 12 B 13 C 20 C 21 C 22 C 23 A 22 A 22 B 20 B 21 B 22 B 23 C 30 C 31 C 32 C 33 A 33 A 33 B 30 B 31 B 32 B 33 initial state Broadcast of A’s 1 st diagonal Local computation 10

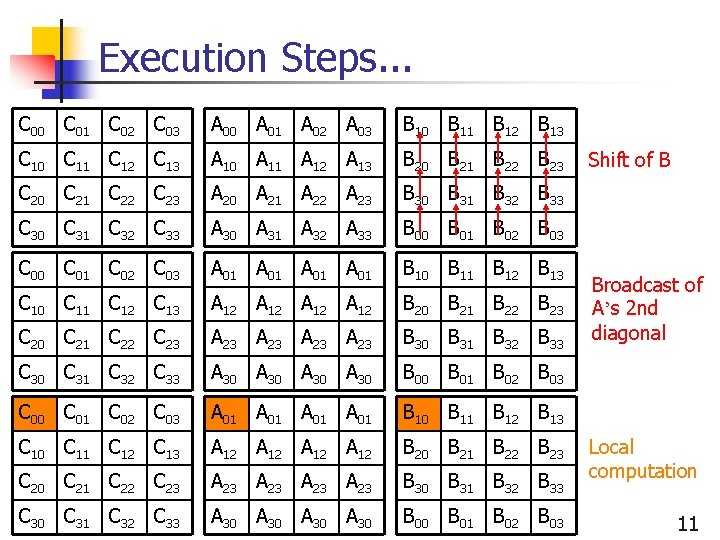
Execution Steps. . . C 00 C 01 C 02 C 03 A 00 A 01 A 02 A 03 B 10 B 11 B 12 B 13 C 10 C 11 C 12 C 13 A 10 A 11 A 12 A 13 B 20 B 21 B 22 B 23 C 20 C 21 C 22 C 23 A 20 A 21 A 22 A 23 B 30 B 31 B 32 B 33 C 30 C 31 C 32 C 33 A 30 A 31 A 32 A 33 B 00 B 01 B 02 B 03 C 00 C 01 C 02 C 03 A 01 A 01 B 10 B 11 B 12 B 13 C 10 C 11 C 12 C 13 A 12 A 12 B 20 B 21 B 22 B 23 C 20 C 21 C 22 C 23 A 23 A 23 B 30 B 31 B 32 B 33 C 30 C 31 C 32 C 33 A 30 A 30 B 00 B 01 B 02 B 03 Shift of B Broadcast of A’s 2 nd diagonal Local computation 11

Fox’s Algorithm // No initial data movement for k = 1 to q-1 in parallel Broadcast A’s kth diagonal Local C = C + A*B Vertical shift of B // No final data movement n Note that there is an additional array to store incoming diagonal block 12

Snyder’s Algorithm (1992) n More complex than Cannon’s or Fox’s n First transposes matrix B n Uses reduction operations (sums) on the rows of matrix C n Shifts matrix B 13

Execution Steps. . . C 00 C 01 C 02 C 03 A 00 A 01 A 02 A 03 B 00 B 01 B 02 B 03 C 10 C 11 C 12 C 13 A 10 A 11 A 12 A 13 B 10 B 11 B 12 B 13 C 20 C 21 C 22 C 23 A 20 A 21 A 22 A 23 B 20 B 21 B 22 B 23 C 30 C 31 C 32 C 33 A 30 A 31 A 32 A 33 B 30 B 31 B 32 B 33 C 00 C 01 C 02 C 03 A 00 A 01 A 02 A 03 B 00 B 10 B 20 B 30 C 10 C 11 C 12 C 13 A 10 A 11 A 12 A 13 B 01 B 11 B 21 B 31 C 20 C 21 C 22 C 23 A 20 A 21 A 22 A 23 B 02 B 12 B 22 B 32 C 30 C 31 C 32 C 33 A 30 A 31 A 32 A 33 B 03 B 13 B 23 B 33 initial state Transpose B Local computation 14

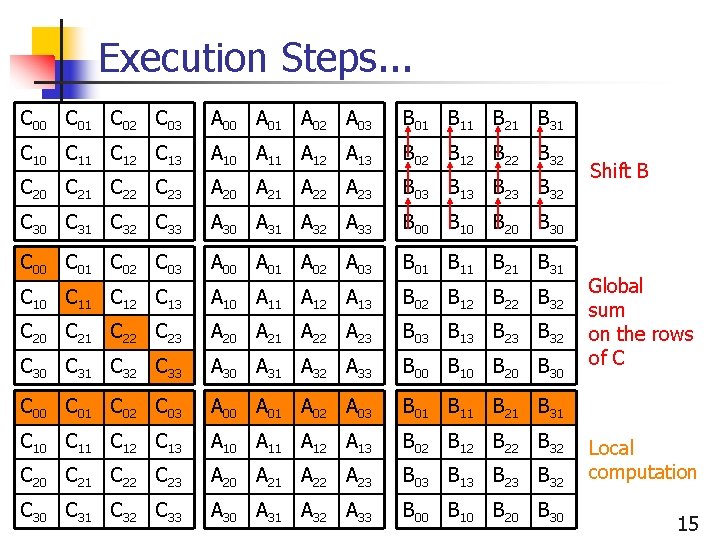
Execution Steps. . . C 00 C 01 C 02 C 03 A 00 A 01 A 02 A 03 B 01 B 11 B 21 B 31 C 10 C 11 C 12 C 13 A 10 A 11 A 12 A 13 B 02 B 12 B 22 B 32 C 20 C 21 C 22 C 23 A 20 A 21 A 22 A 23 B 03 B 13 B 23 B 32 C 30 C 31 C 32 C 33 A 30 A 31 A 32 A 33 B 00 B 10 B 20 B 30 Shift B Global sum on the rows of C Local computation 15

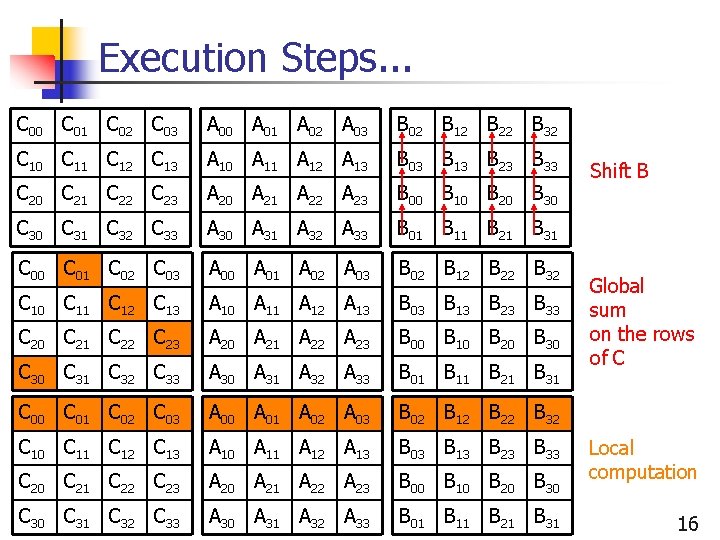
Execution Steps. . . C 00 C 01 C 02 C 03 A 00 A 01 A 02 A 03 B 02 B 12 B 22 B 32 C 10 C 11 C 12 C 13 A 10 A 11 A 12 A 13 B 03 B 13 B 23 B 33 C 20 C 21 C 22 C 23 A 20 A 21 A 22 A 23 B 00 B 10 B 20 B 30 C 31 C 32 C 33 A 30 A 31 A 32 A 33 B 01 B 11 B 21 B 31 C 00 C 01 C 02 C 03 A 00 A 01 A 02 A 03 B 02 B 12 B 22 B 32 C 10 C 11 C 12 C 13 A 10 A 11 A 12 A 13 B 03 B 13 B 23 B 33 C 20 C 21 C 22 C 23 A 20 A 21 A 22 A 23 B 00 B 10 B 20 B 30 C 31 C 32 C 33 A 30 A 31 A 32 A 33 B 01 B 11 B 21 B 31 Shift B Global sum on the rows of C Local computation 16

Complexity Analysis n n Very cumbersome Two models n 4 -port model: every processor can communicate with its 4 neighbors in one step n n n Can match underlying architectures like the Intel Paragon 1 -port model: only one single communication at a time for each processor Both models are assumed bi-directional communication 17

One-port results n Cannon n Fox n Snyder 18

Complexity Results n n n m in these expressions is the block size Expressions for the 4 -port model are MUCH more complicated Remember that this is all for non-cyclic distributions n n formulae and code become very complicated for a full-fledge implementation (nothing divides anything, nothing’s a perfect square, etc. ) Performance analysis of real code is known to be hard n n It is done in a few restricted cases An interesting approach is to use simulation n n Done in Sca. LAPACK (Scalable Linear Algebra PACKage) for instance Essentially: you have written a code so complex you just run a simulation of it to figure out how fast it goes in different cases 19

So What? n n Are we stuck with these rather cumbersome algorithms? Fortunately, there is a much simpler algorithm that’s n not as clever about as good in practice anyway That’s the one you’ll implement in your programming assignment 20

The Outer-Product Algorithm n Remember the sequential matrix multiply for i = 1 to n for j = 1 to n for k = 1 to n Cij = Cij + Aik * Bkj n The first two loops are completely parallel, but the third one isn’t n n i. e. , in shared memory, would require a mutex to protect the writing of shared variable Cij One solution: view the algorithm as “n sequential steps” for k = 1 to n // done in sequence for i = 1 to n // done in parallel for j = 1 to n // done in parallel Cij = Cij + Aik * Bkj 21

The Outer-Product Algorithm for k = 1 to for i = for j Cij n n // done in sequence 1 to n // done in parallel = Cij + Aik * Bkj During the kth step, the processor who “owns” Cij needs Aik and Bkj Therefore, at the kth step, the kth column on A and the kth row of B must be broadcasted over all processors Let us assume a 2 -D block distribution 22

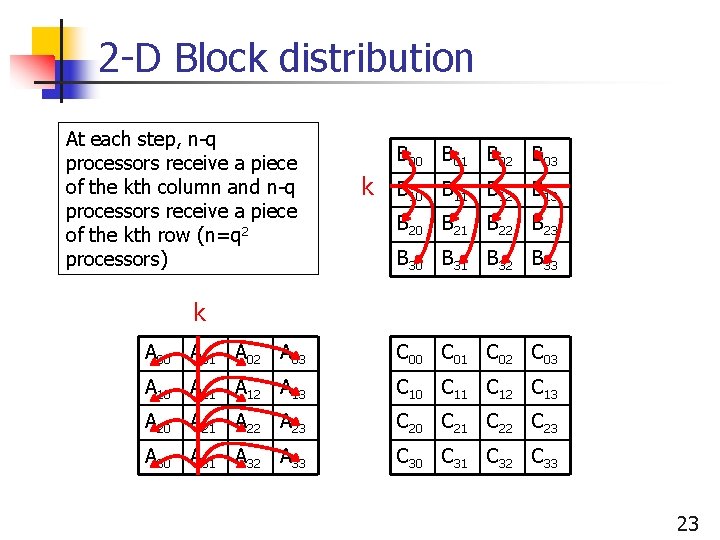
2 -D Block distribution At each step, n-q processors receive a piece of the kth column and n-q processors receive a piece of the kth row (n=q 2 processors) B 00 B 01 B 02 B 03 k B 10 B 11 B 12 B 13 B 20 B 21 B 22 B 23 B 30 B 31 B 32 B 33 k A 00 A 01 A 02 A 03 C 00 C 01 C 02 C 03 A 10 A 11 A 12 A 13 C 10 C 11 C 12 C 13 A 20 A 21 A 22 A 23 C 20 C 21 C 22 C 23 A 30 A 31 A 32 A 33 C 30 C 31 C 32 C 33 23

Outer-Product Algorithm n n n Once everybody has received a piece of row k, everybody can add to the Cij’s they are responsible for And this is repeated n times In your programming assignment: n n Implement the outer-product algorithm Do the “theoretical” performance analysis n with assumptions similar to the ones we have used in class so far 24

Further Optimizations n Send blocks of rows/column to avoid too many small transfers n n Overlap communication and computation by using asynchronous communication n n What is the optimal granularity? How much can be gained? This is a simple and effective algorithm that is not too cumbersome 25

Cyclic 2 -D distributions n What if I want to run on 6 processors? n n n It’s not a perfect square In practice, one makes distributions cyclic to accommodate various numbers of processors How do we do this in 2 -D? n i. e, how do we do a 2 -D block cyclic distribution? 26

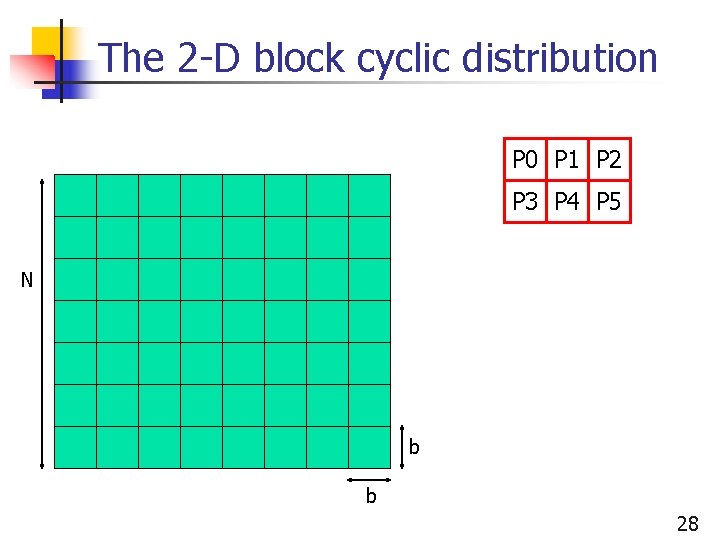
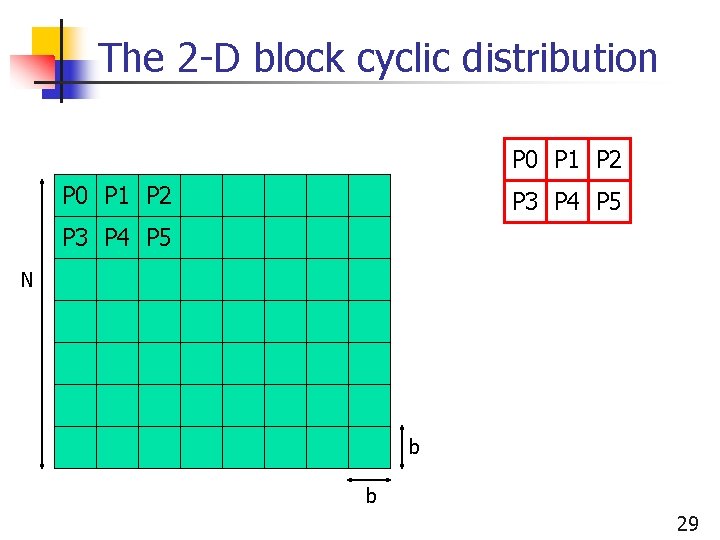
The 2 -D block cyclic distribution n Goal: try to have all the advantages of both the horizontal and the vertical 1 -D block cyclic distribution n Works whichever way the computation “progresses” n n Consider a number of processors p = r * c n n n left-to-right, top-to-bottom, wavefront, etc. arranged in a rxc matrix Consider a 2 -D matrix of size Nx. N Consider a block size b (which divides N) 27

The 2 -D block cyclic distribution P 0 P 1 P 2 P 3 P 4 P 5 N b b 28

The 2 -D block cyclic distribution P 0 P 1 P 2 P 3 P 4 P 5 N b b 29

The 2 -D block cyclic distribution P 0 P 1 P 2 P 0 P 1 P 3 P 4 P 5 P 3 P 4 P 0 P 1 P 2 P 0 P 1 N n n P 3 P 4 P 5 P 3 P 4 n P 0 P 1 P 2 P 0 P 1 n P 3 P 4 P 5 P 3 P 4 P 0 P 1 P 2 P 0 P 1 b Slight load imbalance b n Becomes negligible with many blocks Index computations had better be implemented in separate functions Also: functions that tell a process who its neighbors are Overall, requires a whole infrastructure, but many think you can’t go wrong with this distribution 30