Graphs CS 311 Algorithms Analysis and Design PSU

Graphs CS 311 - Algorithms Analysis and Design PSU

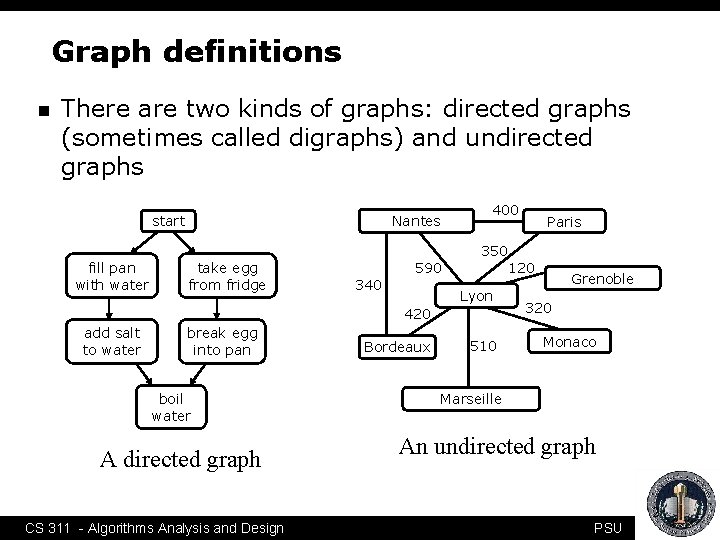
Graph definitions n There are two kinds of graphs: directed graphs (sometimes called digraphs) and undirected graphs Nantes start 400 Paris 350 fill pan with water take egg from fridge 590 340 120 Lyon 420 add salt to water break egg into pan boil water A directed graph Bordeaux 510 Grenoble 320 Monaco Marseille An undirected graph 2 CS 311 - Algorithms Analysis and Design PSU

Graph terminology I n A graph is a collection of nodes (or vertices, singular is vertex) and edges (or arcs) l l n n Each node contains an element Each edge connects two nodes together (or possibly the same node to itself) and may contain an edge attribute A directed graph is one in which the edges have a direction An undirected graph is one in which the edges do not have a direction l l Note: Whether a graph is directed or undirected is a logical distinction—it describes how we think about the graph Depending on the implementation, we may or may not be able to follow a directed edge in the “backwards” direction 3 CS 311 - Algorithms Analysis and Design PSU

Graph terminology II n n n The size of a graph is the number of nodes in it The empty graph has size zero (no nodes) If two nodes are connected by an edge, they are neighbors (and the nodes are adjacent to each other) The degree of a node is the number of edges it has For directed graphs, l If a directed edge goes from node S to node D, we call S the source and D the destination of the edge – The edge is an out-edge of S and an in-edge of D – S is a predecessor of D, and D is a successor of S l l The in-degree of a node is the number of in-edges it has The out-degree of a node is the number of out-edges it has 4 CS 311 - Algorithms Analysis and Design PSU

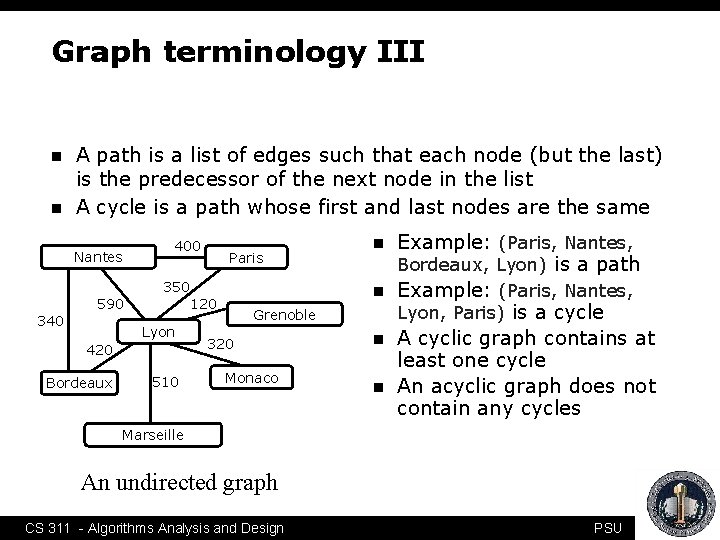
Graph terminology III n n A path is a list of edges such that each node (but the last) is the predecessor of the next node in the list A cycle is a path whose first and last nodes are the same Nantes 400 Paris 350 590 340 420 Bordeaux n 120 Lyon 510 n Grenoble 320 Monaco n n Example: (Paris, Nantes, Bordeaux, Lyon) is a path Example: (Paris, Nantes, Lyon, Paris) is a cycle A cyclic graph contains at least one cycle An acyclic graph does not contain any cycles Marseille An undirected graph 5 CS 311 - Algorithms Analysis and Design PSU

Graph terminology IV n n n An undirected graph is connected if there is a path from every node to every other node A directed graph is strongly connected if there is a path from every node to every other node A directed graph is weakly connected if the underlying undirected graph is connected Node X is reachable from node Y if there is a path from Y to X A subset of the nodes of the graph is a connected component (or just a component) if there is a path from every node in the subset to every other node in the subset 6 CS 311 - Algorithms Analysis and Design PSU

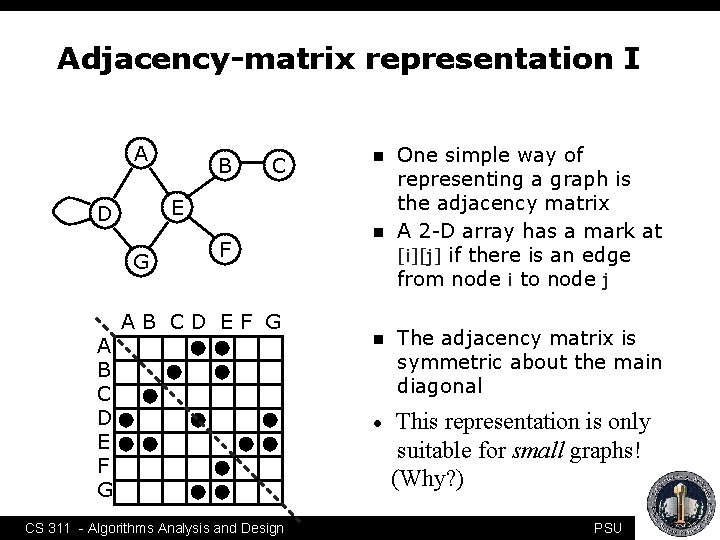
Adjacency-matrix representation I A C n E D G A B C D E F G B F AB CD EF G n n • One simple way of representing a graph is the adjacency matrix A 2 -D array has a mark at [i][j] if there is an edge from node i to node j The adjacency matrix is symmetric about the main diagonal This representation is only suitable for small graphs! (Why? ) 7 CS 311 - Algorithms Analysis and Design PSU

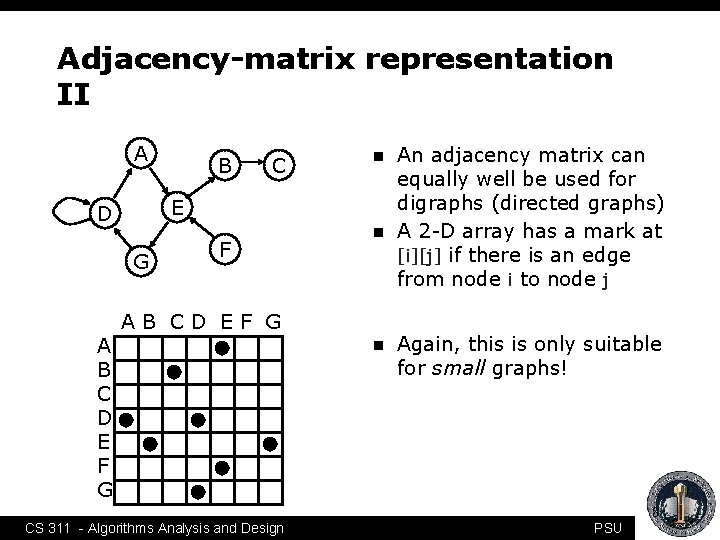
Adjacency-matrix representation II A C n E D G A B C D E F G B F n AB CD EF G n An adjacency matrix can equally well be used for digraphs (directed graphs) A 2 -D array has a mark at [i][j] if there is an edge from node i to node j Again, this is only suitable for small graphs! 8 CS 311 - Algorithms Analysis and Design PSU

Edge-set representation I n An edge-set representation uses a set of nodes and a set of edges l l n n The only other information in a node is its element (that is, its value)—it does not hold information about its edges The only other information in an edge is its source and destination (and attribute, if any) l n n The sets might be represented by, say, linked lists The set links are stored in the nodes and edges themselves If the graph is undirected, we keep links to both nodes, but don’t distinguish between source and destination This representation makes it easy to find nodes from an edge, but you must search to find an edge from a node This is seldom a good representation 9 CS 311 - Algorithms Analysis and Design PSU

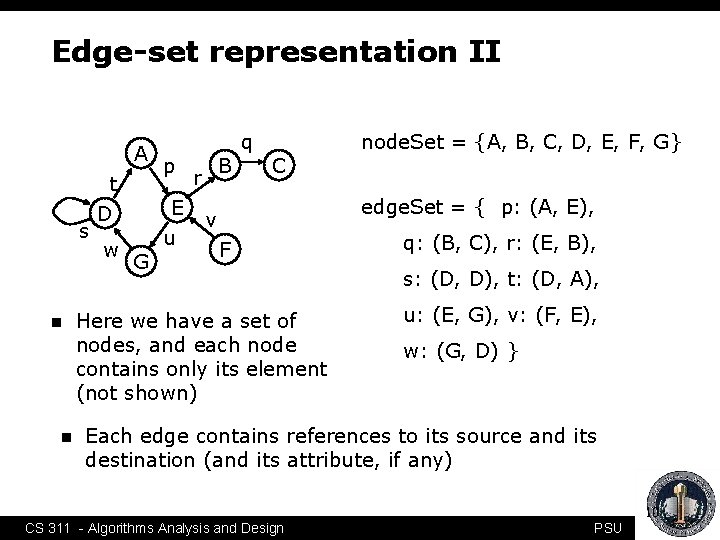
Edge-set representation II A s n n t D w p E G u B r q C node. Set = {A, B, C, D, E, F, G} edge. Set = { p: (A, E), v F Here we have a set of nodes, and each node contains only its element (not shown) q: (B, C), r: (E, B), s: (D, D), t: (D, A), u: (E, G), v: (F, E), w: (G, D) } Each edge contains references to its source and its destination (and its attribute, if any) 10 CS 311 - Algorithms Analysis and Design PSU

Adjacency-set representation I n An adjacency-set representation uses a set of nodes l l n Each node contains a reference to the set of its edges For a directed graph, a node might only know about (have references to) its out-edges Thus, there is not one single edge set, but rather a separate edge set for each node l Each edge would contain its attribute (if any) and its destination (and possibly its source) 11 CS 311 - Algorithms Analysis and Design PSU

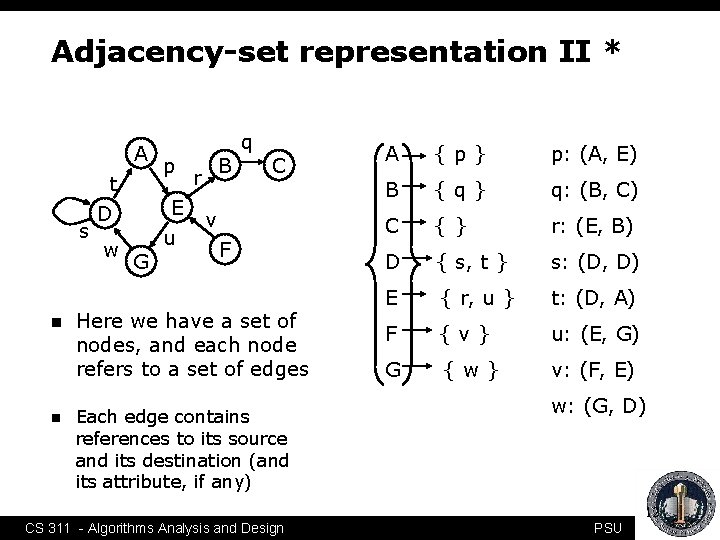
Adjacency-set representation II * A s n n t D w p E G u B r q C v F Here we have a set of nodes, and each node refers to a set of edges Each edge contains references to its source and its destination (and its attribute, if any) A {p} p: (A, E) B {q} q: (B, C) C {} r: (E, B) D { s, t } s: (D, D) E { r, u } t: (D, A) F {v} u: (E, G) G {w} v: (F, E) w: (G, D) 12 CS 311 - Algorithms Analysis and Design PSU

Adjacency-set representation III n If the edges have no associated attribute, there is no need for a separate Edge class l l n n Instead, each node can refer to a set of its neighbors In this representation, the edges would be implicit in the connections between nodes, not a separate data structure For an undirected graph, the node would have references to all the nodes adjacent to it For a directed graph, the node might have: l l references to all the nodes adjacent to it, or references to only those adjacent nodes connected by an out-edge from this node 13 CS 311 - Algorithms Analysis and Design PSU

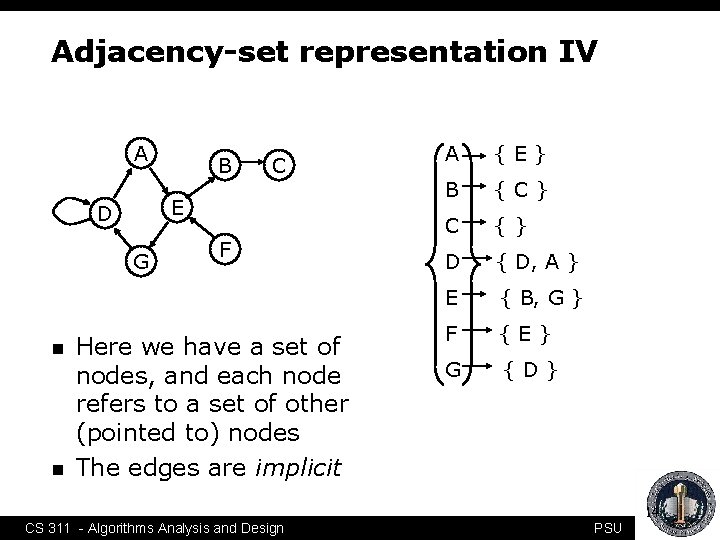
Adjacency-set representation IV A G n C E D n B F Here we have a set of nodes, and each node refers to a set of other (pointed to) nodes The edges are implicit A {E} B {C} C {} D { D, A } E { B, G } F {E} G {D} 14 CS 311 - Algorithms Analysis and Design PSU

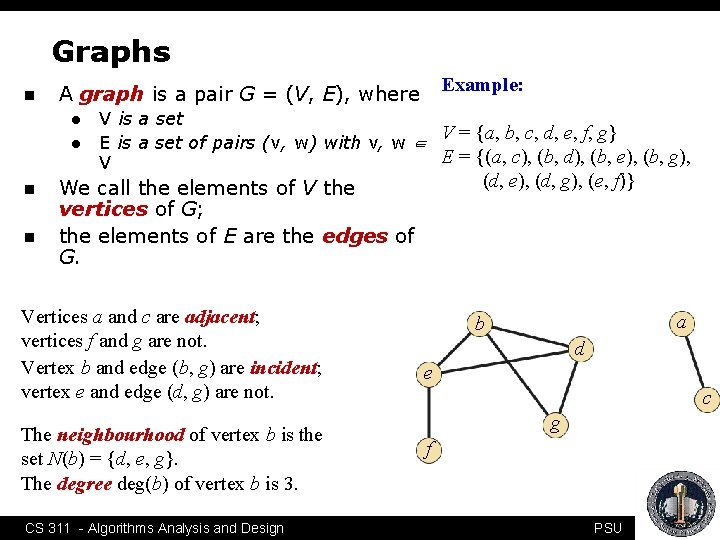
Graphs n l l n n Example: A graph is a pair G = (V, E), where V is a set V = {a, b, c, d, e, f, g} E is a set of pairs (v, w) with v, w ∈ E = {(a, c), (b, d), (b, e), (b, g), V (d, e), (d, g), (e, f)} We call the elements of V the vertices of G; the elements of E are the edges of G. Vertices a and c are adjacent; vertices f and g are not. Vertex b and edge (b, g) are incident; vertex e and edge (d, g) are not. The neighbourhood of vertex b is the set N(b) = {d, e, g}. The degree deg(b) of vertex b is 3. CS 311 - Algorithms Analysis and Design a b d e c g f PSU

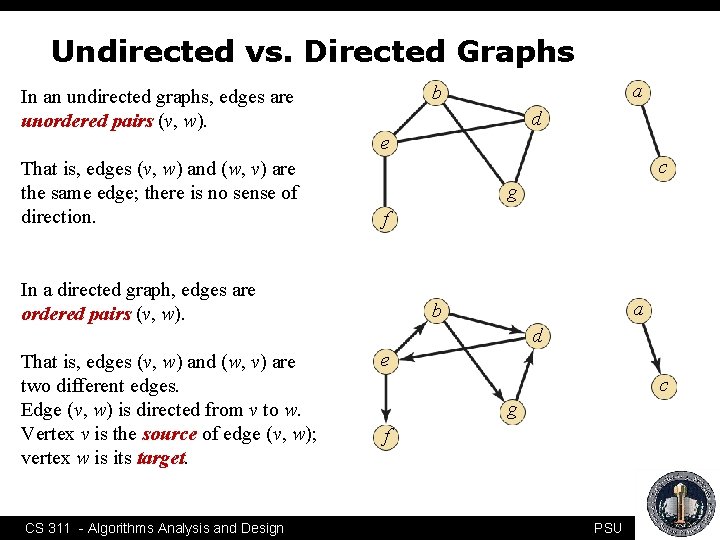
Undirected vs. Directed Graphs In an undirected graphs, edges are unordered pairs (v, w). That is, edges (v, w) and (w, v) are the same edge; there is no sense of direction. d e c g f In a directed graph, edges are ordered pairs (v, w). That is, edges (v, w) and (w, v) are two different edges. Edge (v, w) is directed from v to w. Vertex v is the source of edge (v, w); vertex w is its target. CS 311 - Algorithms Analysis and Design a b d e c g f PSU

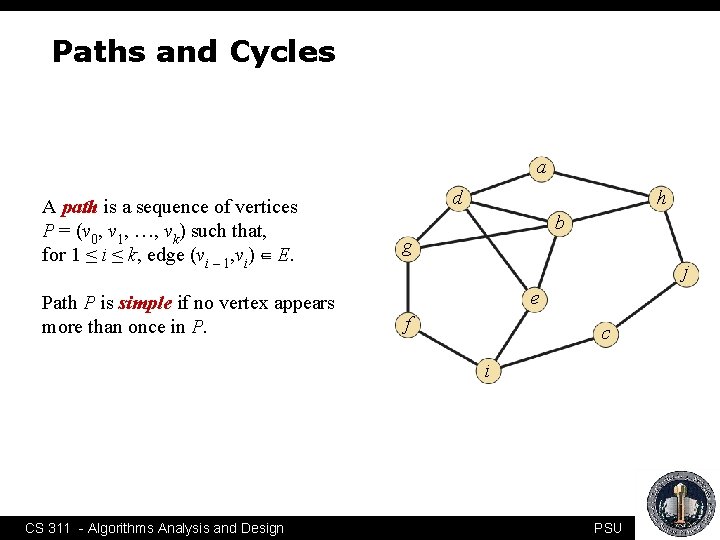
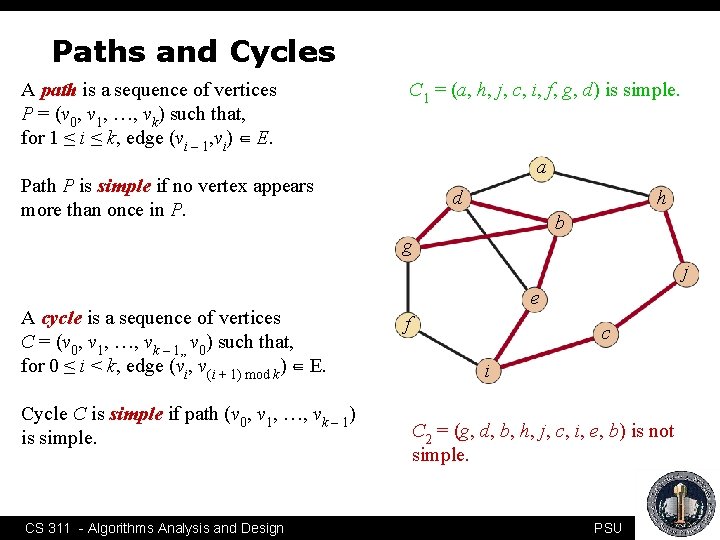
Paths and Cycles a A path is a sequence of vertices P = (v 0, v 1, …, vk) such that, for 1 ≤ i ≤ k, edge (vi – 1, vi) ∈ E. Path P is simple if no vertex appears more than once in P. d h b g j e f c i CS 311 - Algorithms Analysis and Design PSU

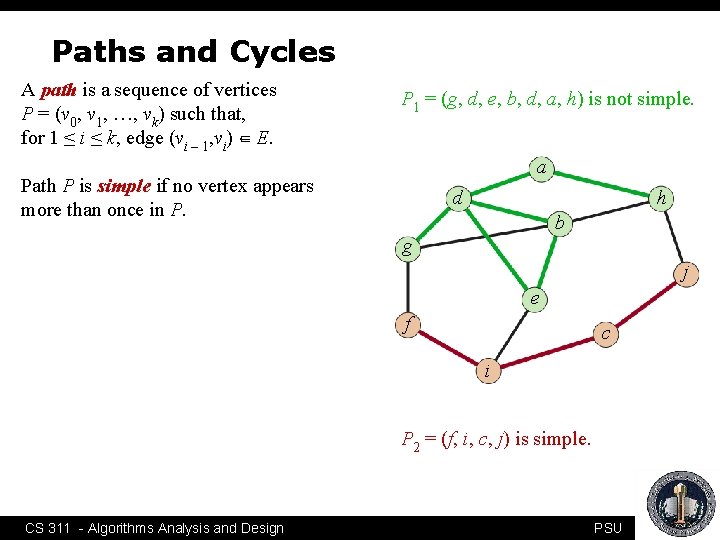
Paths and Cycles A path is a sequence of vertices P = (v 0, v 1, …, vk) such that, for 1 ≤ i ≤ k, edge (vi – 1, vi) ∈ E. P 1 = (g, d, e, b, d, a, h) is not simple. a Path P is simple if no vertex appears more than once in P. d h b g j e f c i P 2 = (f, i, c, j) is simple. CS 311 - Algorithms Analysis and Design PSU

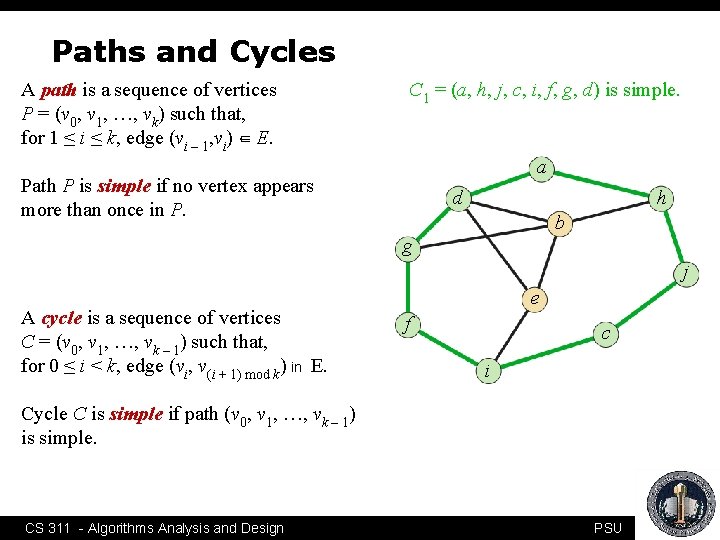
Paths and Cycles A path is a sequence of vertices P = (v 0, v 1, …, vk) such that, for 1 ≤ i ≤ k, edge (vi – 1, vi) ∈ E. C 1 = (a, h, j, c, i, f, g, d) is simple. a Path P is simple if no vertex appears more than once in P. d h b g j A cycle is a sequence of vertices C = (v 0, v 1, …, vk – 1) such that, for 0 ≤ i < k, edge (vi, v(i + 1) mod k) in E. e f c i Cycle C is simple if path (v 0, v 1, …, vk – 1) is simple. CS 311 - Algorithms Analysis and Design PSU

Paths and Cycles A path is a sequence of vertices P = (v 0, v 1, …, vk) such that, for 1 ≤ i ≤ k, edge (vi – 1, vi) ∈ E. C 1 = (a, h, j, c, i, f, g, d) is simple. a Path P is simple if no vertex appears more than once in P. d h b g j A cycle is a sequence of vertices C = (v 0, v 1, …, vk – 1, , v 0) such that, for 0 ≤ i < k, edge (vi, v(i + 1) mod k) ∈ E. Cycle C is simple if path (v 0, v 1, …, vk – 1) is simple. CS 311 - Algorithms Analysis and Design e f c i C 2 = (g, d, b, h, j, c, i, e, b) is not simple. PSU

Subgraphs n A graph H = (W, F) is a subgraph of a graph G = (V, E) if W in V and F in E. CS 311 - Algorithms Analysis and Design PSU

Subgraphs n A graph H = (W, F) is a subgraph of a graph G = (V, E) if W ⊆ V and F ⊆ E. CS 311 - Algorithms Analysis and Design PSU

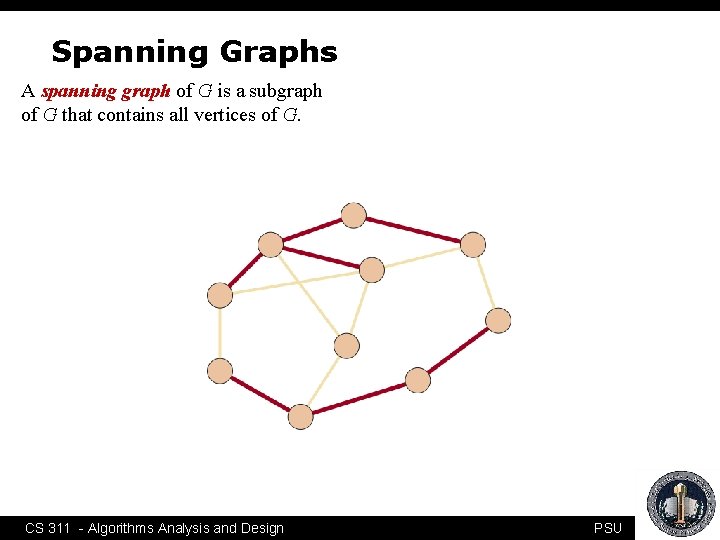
Spanning Graphs A spanning graph of G is a subgraph of G that contains all vertices of G. CS 311 - Algorithms Analysis and Design PSU

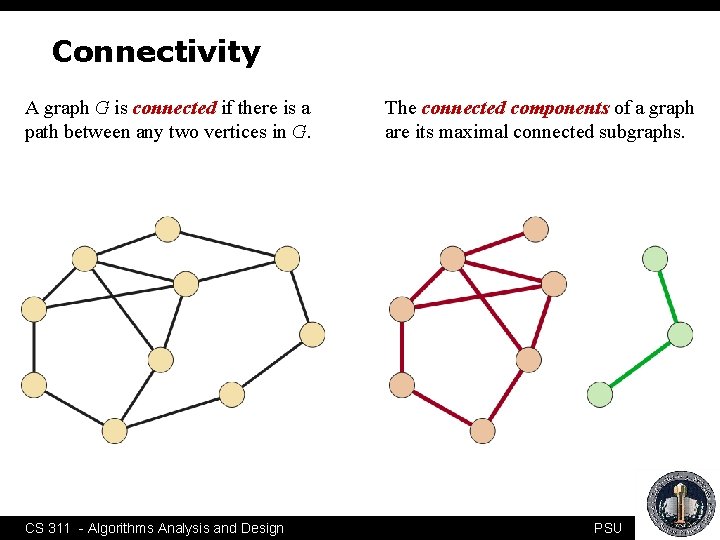
Connectivity A graph G is connected if there is a path between any two vertices in G. CS 311 - Algorithms Analysis and Design The connected components of a graph are its maximal connected subgraphs. PSU

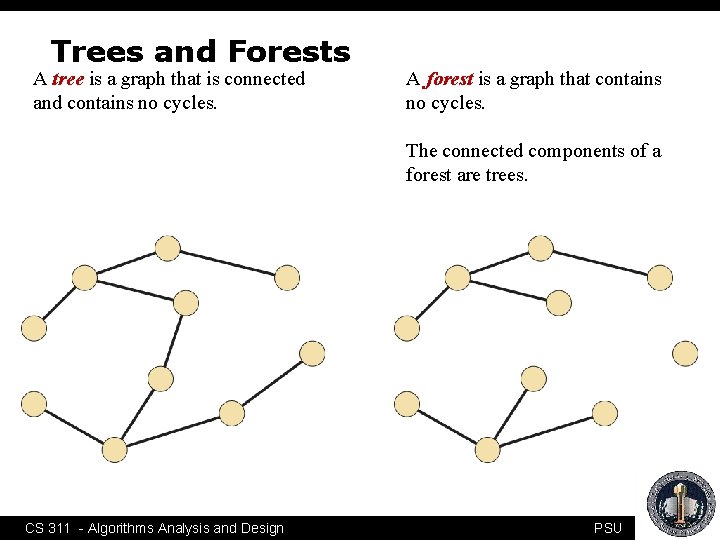
Trees and Forests A tree is a graph that is connected and contains no cycles. A forest is a graph that contains no cycles. The connected components of a forest are trees. CS 311 - Algorithms Analysis and Design PSU

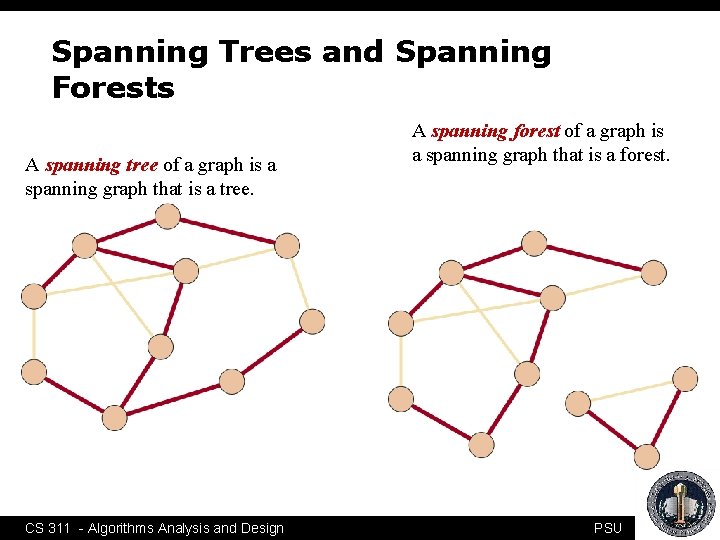
Spanning Trees and Spanning Forests A spanning tree of a graph is a spanning graph that is a tree. CS 311 - Algorithms Analysis and Design A spanning forest of a graph is a spanning graph that is a forest. PSU

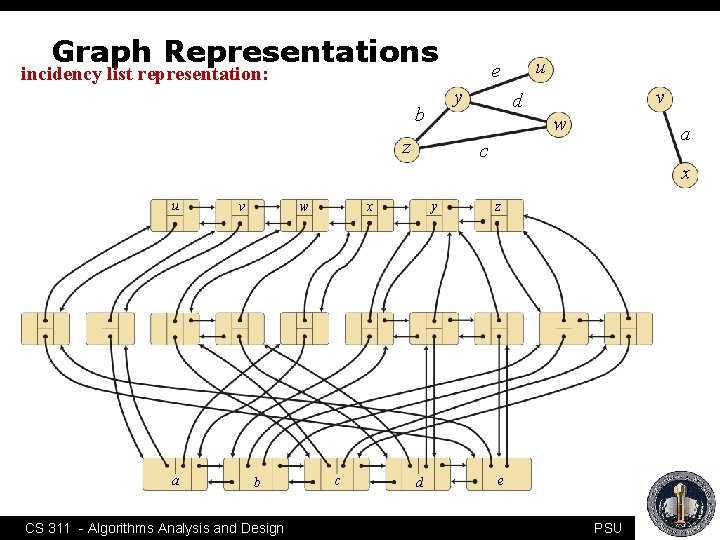
Graph Representations y b a v w b CS 311 - Algorithms Analysis and Design a c x c v d w z u u e incidency list representation: y d x z e PSU

Searching a graph n With certain modifications, any tree search technique can be applied to a graph l n The difference is that a graph may have cycles l n n This includes depth-first, breadth-first, depth-first iterative deepening, and other types of searches We don’t want to search around in a cycle To avoid getting caught in a cycle, we must keep track of which nodes we have already explored There are two basic techniques for this: l l Keep a set of already explored nodes, or Mark the node itself as having been explored 28 CS 311 - Algorithms Analysis and Design PSU

Example: Depth-first search n Here is how to do DFS on a tree: Put the root node on a stack; while (stack is not empty) { remove a node from the stack; if (node is a goal node) return success; put all children of the node onto the stack; } return failure; n Here is how to do DFS on a graph: Put the starting node on a stack; while (stack is not empty) { remove a node from the stack; if (node has already been visited) continue; if (node is a goal node) return success; put all adjacent nodes of the node onto the stack; } return failure; 29 CS 311 - Algorithms Analysis and Design PSU

Finding connected components n A depth-first search can be used to find connected components of a graph l l n A connected component is a set of nodes; therefore, A set of connected components is a set of sets of nodes To find the connected components of a graph: while there is a node not assigned to a component { put that node in a new component do a DFS from the node, and put every node reached into the same component } 30 CS 311 - Algorithms Analysis and Design PSU

Graph applications n Graphs can be used for: l l l l l Finding a route to drive from one city to another Finding connecting flights from one city to another Determining least-cost highway connections Designing optimal connections on a computer chip Implementing automata Implementing compilers Doing garbage collection Representing family histories Pert charts Playing games 31 CS 311 - Algorithms Analysis and Design PSU

Shortest-path n n Suppose we want to find the shortest path from node X to node Y It turns out that, in order to do this, we need to find the shortest path from X to all other nodes l l n Why? If we don’t know the shortest path from X to Z, we might overlook a shorter path from X to Y that contains Z Dijkstra’s Algorithm finds the shortest path from a given node to all other reachable nodes 32 CS 311 - Algorithms Analysis and Design PSU

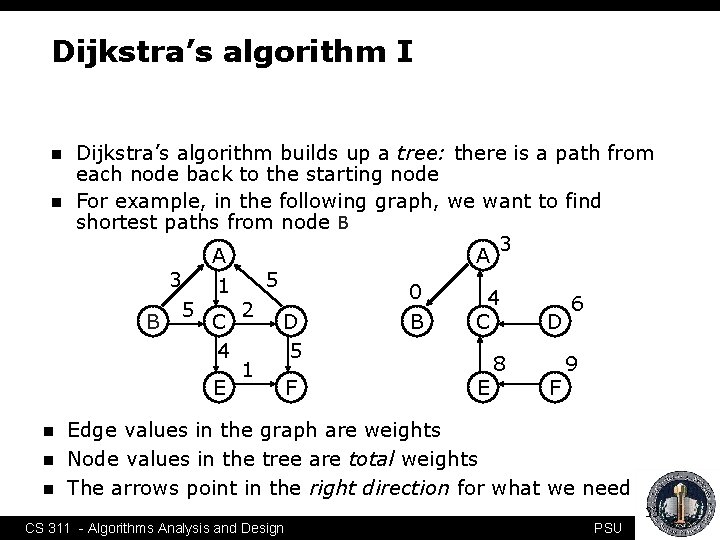
Dijkstra’s algorithm I n n n Dijkstra’s algorithm builds up a tree: there is a path from each node back to the starting node For example, in the following graph, we want to find shortest paths from node B 3 A A 3 5 1 0 4 6 5 2 B C D 4 5 8 9 1 E F Edge values in the graph are weights Node values in the tree are total weights The arrows point in the right direction for what we need 33 CS 311 - Algorithms Analysis and Design PSU

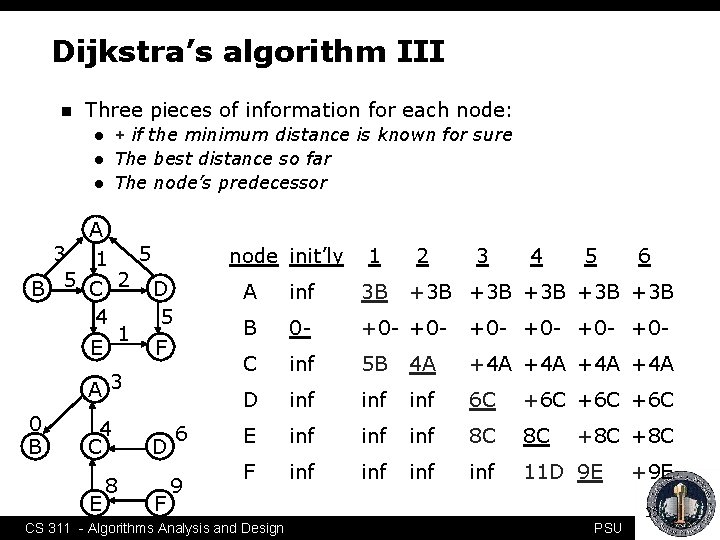
Dijkstra’s algorithm II n For each vertex v, Dijkstra’s algorithm keeps track of three pieces of information: l l l n A boolean telling whether we know the shortest path to that node (initially true only for the starting node) The length of the shortest path to that node known so far (0 for the starting node) The predecessor of that node along the shortest known path (unknown for all nodes) Dijkstra’s algorithm proceeds in phases—at each step: l l l From the vertices for which we don’t know the shortest path, pick a vertex v with the smallest distance known so far Set v’s “known” field to true For each vertex w adjacent to v, test whether its distance so far is greater than v’s distance plus the distance from v to w; if so, set w’s distance to the new distance and w’s predecessor to v 34 CS 311 - Algorithms Analysis and Design PSU

Dijkstra’s algorithm III n Three pieces of information for each node: + if the minimum distance is known for sure The best distance so far The node’s predecessor l l l A 3 5 1 B 5 C 2 D 4 5 1 E F node init’ly A 3 0 B 4 C E 8 D F 6 9 1 2 3 4 5 6 A inf 3 B B 0 - +0 - +0 - +0 - C inf 5 B 4 A +4 A +4 A D inf inf 6 C +6 C +6 C E inf inf 8 C 8 C F inf inf 11 D 9 E CS 311 - Algorithms Analysis and Design +3 B +3 B +3 B +8 C +9 E 35 PSU

Summary n n A graph may be directed or undirected The edges (=arcs) may have weights or contain other data, or they may be just connectors Similarly, the nodes (=vertices) may or may not contain data There are various ways to represent graphs l l n The “best” representation depends on the problem to be solved You need to consider what kind of access needs to be quick or easy Many tree algorithms can be modified for graphs l Basically, this means some way to recognize cycles 36 CS 311 - Algorithms Analysis and Design PSU

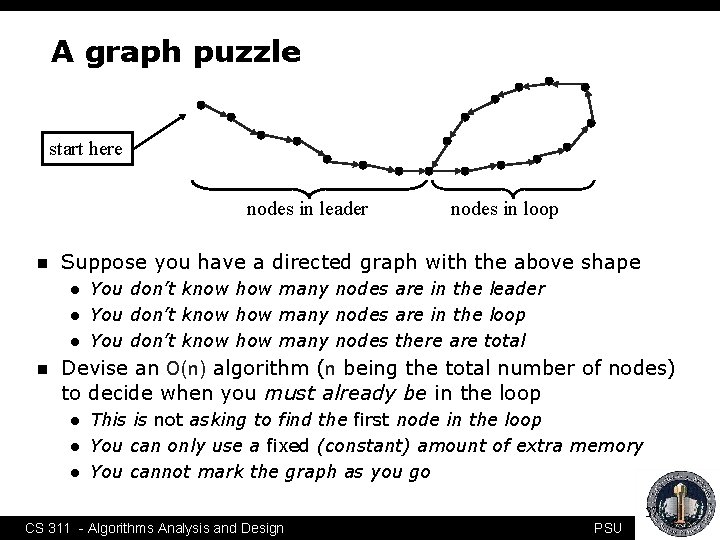
A graph puzzle start here nodes in leader n Suppose you have a directed graph with the above shape l l l n nodes in loop You don’t know how many nodes are in the leader You don’t know how many nodes are in the loop You don’t know how many nodes there are total Devise an O(n) algorithm (n being the total number of nodes) to decide when you must already be in the loop l l l This is not asking to find the first node in the loop You can only use a fixed (constant) amount of extra memory You cannot mark the graph as you go 37 CS 311 - Algorithms Analysis and Design PSU