Graph Algorithms n Representations of graphsundirected graph n

Graph Algorithms

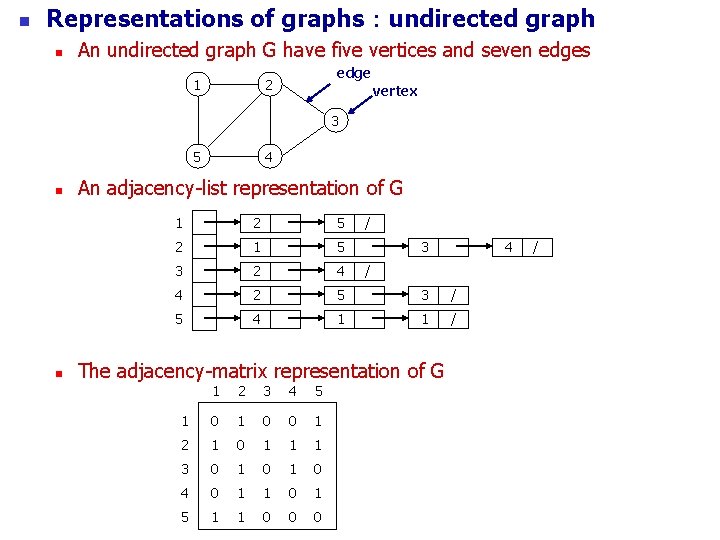
n Representations of graphs：undirected graph n An undirected graph G have five vertices and seven edges 1 edge 2 vertex 3 5 n n 4 An adjacency-list representation of G 1 2 5 / 2 1 5 3 2 4 4 2 5 3 / 5 4 1 1 / 3 / The adjacency-matrix representation of G 1 2 3 4 5 1 0 0 1 2 1 0 1 1 1 3 0 1 0 4 0 1 1 0 1 5 1 1 0 0 0 4 /

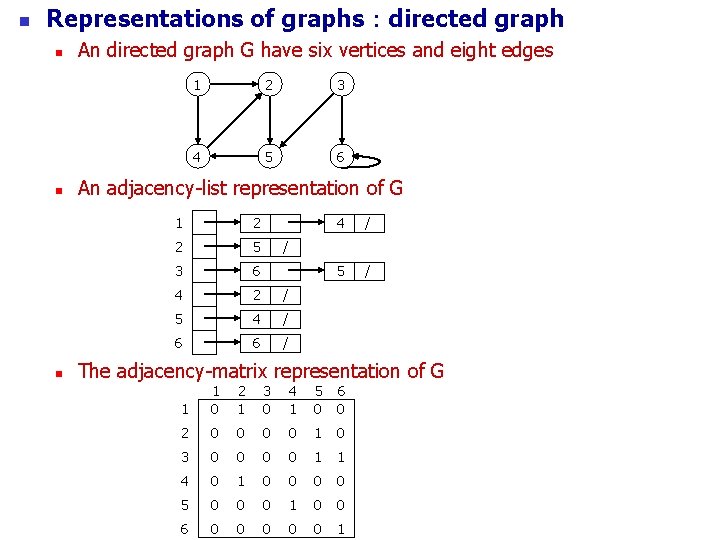
n Representations of graphs：directed graph n n n An directed graph G have six vertices and eight edges 1 2 3 4 5 6 An adjacency-list representation of G 1 2 2 5 3 6 4 2 / 5 4 / 6 6 / 4 / 5 / / The adjacency-matrix representation of G 1 1 0 2 1 3 0 4 1 5 0 6 0 2 0 0 1 0 3 0 0 1 1 4 0 1 0 0 5 0 0 0 1 0 0 6 0 0 0 1

BFS(G, s) 1. for each vertex u∈ G. V-{s} 2. u. color = WHITE 3. u. d = ∞ 4. u. π = NIL 5. s. color = GREEN 6. s. d = 0 7. s. π = NIL 8. Q = empty 9. Enqueue(Q, s) 10. while Q ≠ empty 11. u = Dequeue(Q) 12. for each v∈ G. Adj[u] 13. if v. color == WHITE 14. v. color = GREEN 15. v. d = u. d + 1 16. v. π = u 17. Enqueue(Q, v) 18. u. color = BLACK Time Complexity: O(|E|+|V|) Elementary Graph Algorithms 4

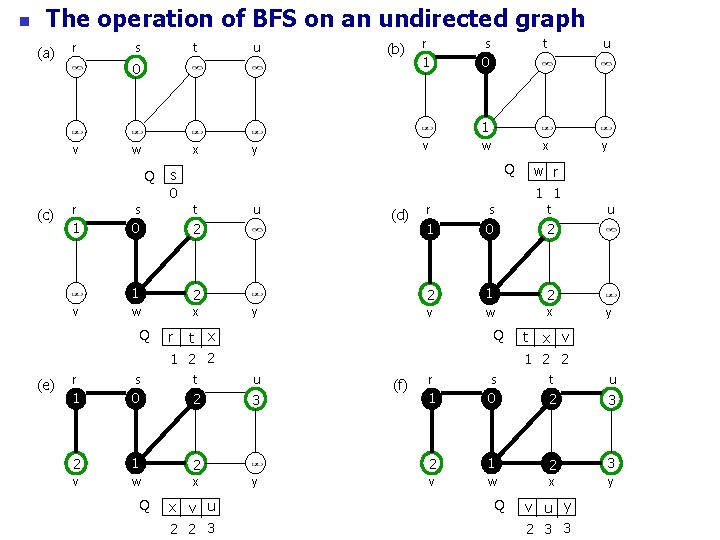
n The operation of BFS on an undirected graph (a) r s t u (b) 0 r s 1 0 t u x y 1 v x w Q (c) (e) Q s t 1 0 2 1 2 w x Q u (d) y s t 1 0 2 2 1 2 v w x Q t x 1 2 2 s t u 1 0 2 3 2 1 2 v w x x v u 2 2 3 y (f) w r 1 1 r r r Q w s 0 r v v y u y x v 1 2 2 t r s t u 1 0 2 3 2 1 2 3 v w x y Q v u y 2 3 3

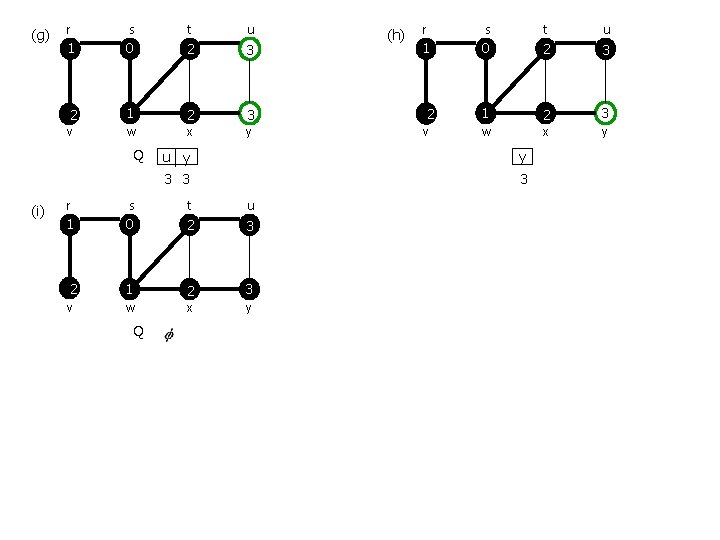
(g) r s t u 1 0 2 3 1 2 w x 2 v 2 Q (i) r s t u 1 0 2 3 3 2 1 2 3 y v w x y u y 3 3 y 3 r s t u 1 0 2 3 2 1 2 3 v w x y Q (h)

n Breadth-first search： n n n Initially, vertices are colored white. Discovered vertices are colored green. When done, discovered vertices are colored black. u. d stores the distance from s to u. u. π is a predecessor to u on its shortest path. Q is a first-in first-out queue. p 7.

n Properties of Breadth-first search： n n After execution of BFS, all nodes reachable from the source s are colored black. After execution of BFS, v. d is the distance of a shortest path from the source s to v for vertices v reachable from s. After execution of BFS, if v is reachable from s, then one of the shortest paths to v passes through the edge( v. π, v) at the end. After execution of BFS, the edges( v. π, v ) for v reachable from s form a breadth-first tree. p 8.

n Lemma 22. 1： n n n G=(V, E)：a directed or undirected graph. s：an arbitrary vertex ： the shortest-path distance from s to v. Then for any Proof： u 1 s v p 9.

n Lemma 22. 2： n n n G=(V, E)：a directed or undirected graph. s：an arbitrary vertex u. d： the distance from s to u computed by the algorithm Suppose that BFS is run on G from s. Then on termination, for each vertex v ∈ V, the value v. d computed by BFS satisfies v. d ≥ δ (s, v). Proof： By induction on the number Enqueue operations. Basis： when s is placed in Q. s. d =0 = δ(s, s) for all Induction Step： Consider a white vertex v discovered during the search from a vertex u. Inductive hypothesis implies u. d ≥ δ (s, u). By Lemma 22. 1, v. d = u. d +1 ≥ δ(s, u) + 1 ≥ δ(s, v) From then on, v. d will not be changed again.

n head Lemma 22. 3： n tail Q：<v 1, v 2, …, vr>~ the queue when BFS executes on a graph G=(V, E). Then and for i=1, 2, …, r-1. Proof： By induction on the number of queue operations. Basis： when Q has only s. Induction Step： 1>： after dequeue： v 2 becomes the new head in Q. by inductive hypothesis. 2>：after enqueue a new vertex v into the Q. Let vr+1 be v. neighbors Note that u’s adjacency list is being scanned and u is just removed. Thus, And The rest , for i=1, …, r-1, remain unaffected.

n Thm 22. 5: (Correctness of BFS) n n 1. During the execution of BFS on G=(V, E), BFS discovers every vertex v ∈ V that is reachable from s, and on termination v. d = δ(s, v) 2. For any vertex v ≠ s reachable from s, one of the shortest paths from s to v is the shortest path from s to v. π followed by the edge ( v. π, v). p 12.

Proof： If v unreachable from s, s. d (s, v)=. By BFS, v is never discovered. By contradiction, suppose some vertex has a d value not equal to its shortest distance. Let v be the vertex with minimum (s, v) that has an incorrect d value. Let u be v’s immediate predecessor on the shortest path from s to v. So (s, v) = (s, u) +1. Because (s, u) < (s, v), we have u. d= (s, u). (*) Thus v. d > (s, v) = (s, u) + 1= u. d + 1. Consider the time when BFS chooses to dequeue u from Q. At this time v is either white, gray or black. Case 1: (v is white) line 15 set v. d = u. d + 1 ---contradicting (*) Case 2: (v is black) v is already not in Q, thus v. d u. d --- contradicting (*) Case 3: (v is gray) v became gray while dequeuing some vertex w, which was removed earlier than u. Thus v. d= w. d +1 and w. d u. d and so v. d u. d + 1 – again a contradiction! Thus we conclude v. d = (s, v) for all v. All vertices reachable from s must be discovered. If v. π =u, then v. d = u. d +1. Thus, we can obtain a shortest path from s to v by taking a shortest path from s to v. π then traversing the edge (v. π, v).

n Breadth-first trees: For a graph G=(V, E) with source s, define the predecessor subgraph of G as G’=(V’, E’), where V’ = { v V: v. π ≠ NIL} {s} and E’ = {(v. π, v): v V’- {s}}. G’ is a BF tree if V’ consists of the vertices from s to v in G’ and, for all v in V’, there is a unique simple path from s to v, which is also a shortest path from s to v in G. Lemma 22. 6: When applied to a graph G=(V, E), procedure BFS construct π so that G’= (V’, E’) is a BF tree. Proof: Line 16 of BFS sets v. π =u iff (u, v) ∈ E and (s, v) < . Thus V’ consists of the vertices in V reachable from s. Since G’ forms a tree, it contains a unique path from s to each vertex in V’. By Thm 22. 5, inductively, we have that every such path is a shortest path.

Print path演算法 可在執行過BFS演算法的圖上印出s到v的最短路徑。 如無路徑也會印出沒有路徑的訊息。 Print-Path(G, s, v) 1. if v == s 2. print s 3. elseif v. π == NIL 4. print “no path from” s “to” v 5. else Print-Path(G, s, v. π) 6. print v n Elementary Graph Algorithms 15 p 15.

Depth-first search n n n Nodes are initially white Nodes become gray when first discovered Nodes become black when they are done v. d records when v is first discovered v. f records when v is done u. d< u. f p 16.

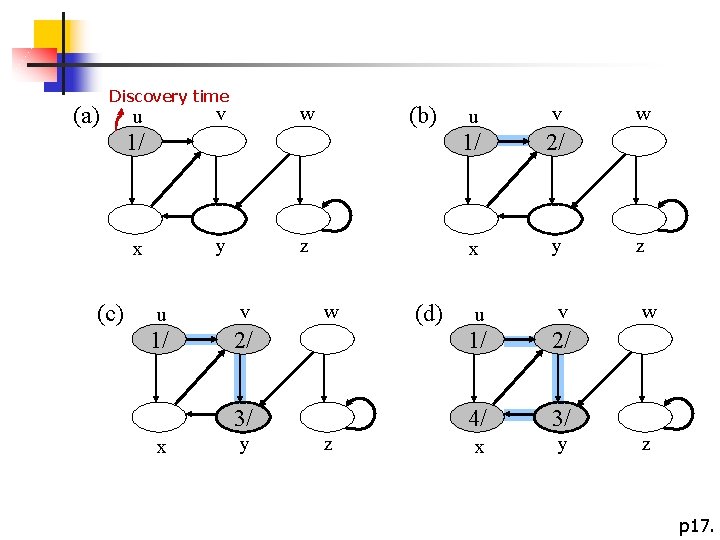
(a) Discovery time v u (b) w 1/ y x (c) z (d) v 1/ 2/ x y z u v w u v 1/ 2/ 3/ 4/ 3/ x y w u z w z p 17.

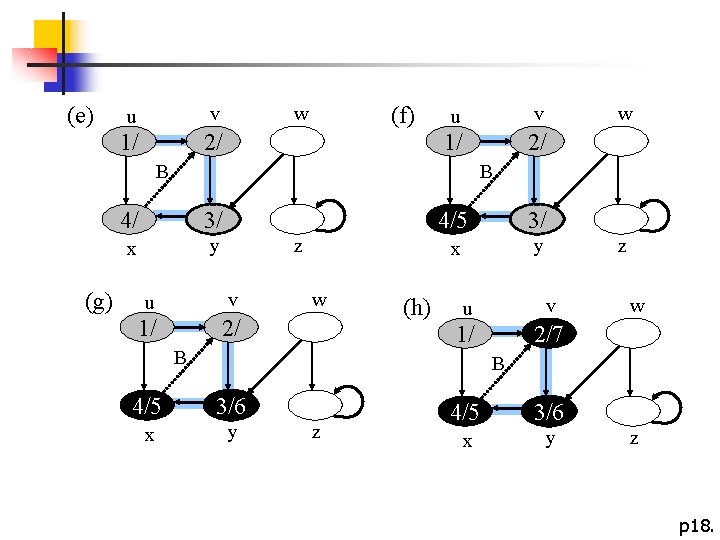
(e) u v 1/ 2/ (f) w u v 1/ 2/ B (g) w B 4/ 3/ x y z u v 1/ 2/ w B (h) 4/5 3/ x y z u v 1/ 2/7 w B 4/5 3/6 x y z p 18.

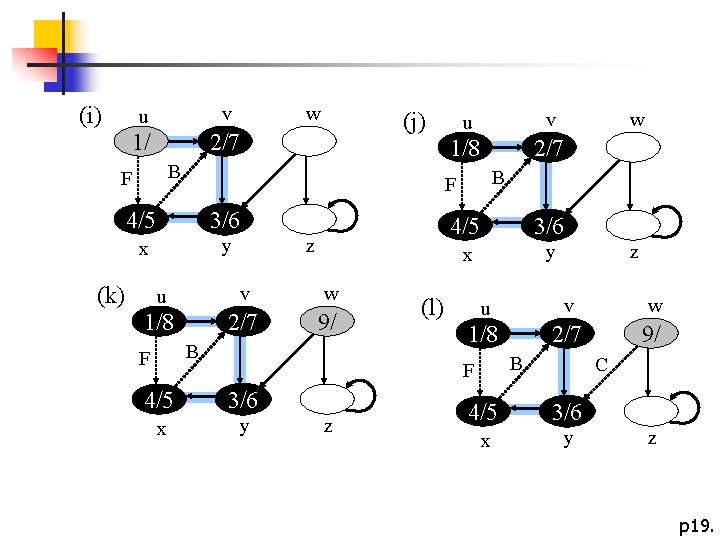
(i) u v w 1/ 2/7 (j) B F 3/6 x y z u v w 1/8 2/7 9/ B F v 1/8 2/7 4/5 3/6 x y (l) 3/6 x y z z u v w 1/8 2/7 9/ B F 4/5 w B F 4/5 (k) u C 4/5 3/6 x y z p 19.

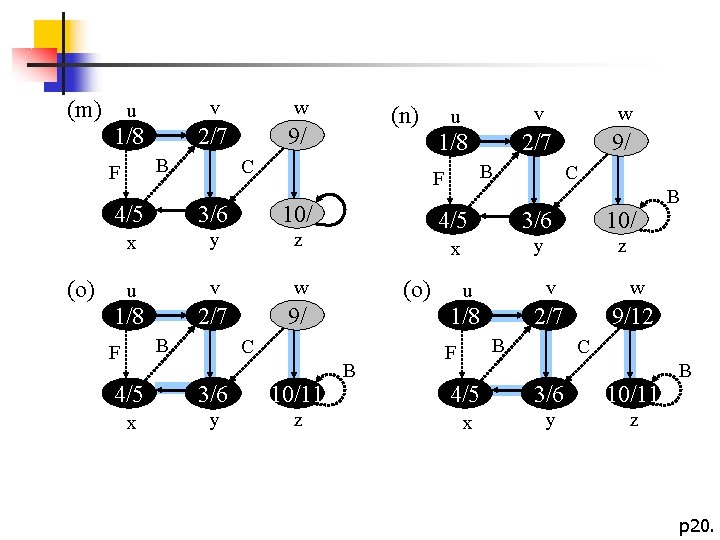
(m) u v w 1/8 2/7 9/ B F C 3/6 10/ x y z u v w 1/8 2/7 9/ B F 4/5 (o) (n) 4/5 3/6 10/11 x y z 4/5 3/6 10/ x y z (o) C B C u v w 1/8 2/7 9/12 B F B C 4/5 3/6 10/11 x y z B p 20.

n (u, v) n n n Back edges: if u is connected to an ancestor v in a depthfirst tree. (eg self-loop) Forward edges: if u is connected to an descendant v in a depth-first tree. Cross edges: if u is not connected to an ancestor v in the same depth-first tree. OR if v is not connected to an ancestor u in the same depth-first tree. OR if u and v belong to different depth-first trees. p 21.

DFS演算法 DFS(G) 1. for each vertex u∈ G. V 2. do u. color = WHITE 3. u. π = NIL 4. time = 0 5. for each vertex u ∈ G. V 6. if u. color == WHITE 7. DFS-Visit(G, u) Elementary Graph Algorithms 22 p 22.

DFS-Visit演算法 DFS-Visit(G, u) 1. time = time+1 //u has just been discovered 2. u. d = time 3. u. color = GRAY 4. for each v ∈ G. Adj[u] //explore edge (u, v) 5. if v. color == WHITE 6. v. π = u 7. DFS-Visit(G, v) 8. u. color = BLACK //DFS-Visit(G, u) is done 9. time = time + 1 10. u. f = time Elementary Graph Algorithms 23 p 23.

n n n The running time of DFS is O(V+E) After execution of DFS, all nodes are colored black After execution of DFS, the edges( v. �� , v) form a collection of depth-first tree, called a depthfirst forest. p 24.

n Edge Classification n 1. Tree edges( u, v ): u was discovered first using ( u, v ) n 2. Back edges( u, v ): v is an ancestor of u in the DFS tree n 3. Forward edges( u, v ): v is a descendent of u, not a tree edge n 4. Cross edges( u, v ): Other edges n Example n In a depth-first search of an undirected graph, every edge is either a tree edge or a back edge p 25.

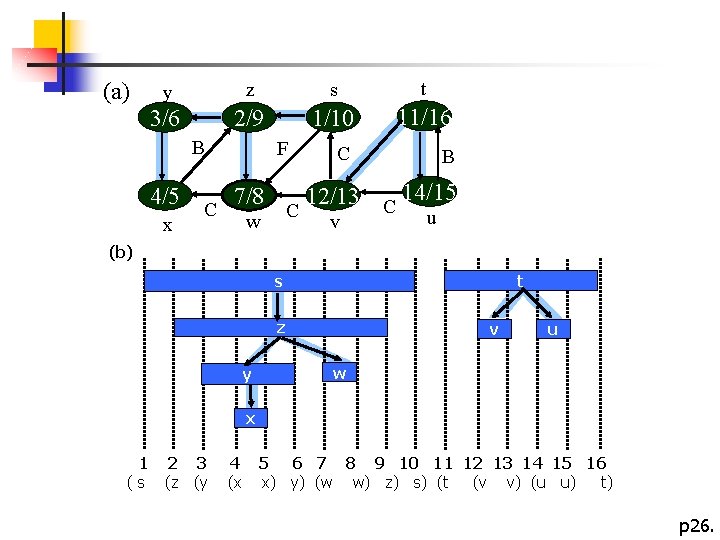
(a) y z s t 3/6 2/9 1/10 11/16 C B B 4/5 x C F 12/13 C 14/15 C u 7/8 w v (b) t s z y v u w x 1 (s 2 3 (z (y 4 (x 5 6 7 8 9 10 11 12 13 14 15 16 x) y) (w w) z) s) (t (v v) (u u) t) p 26.

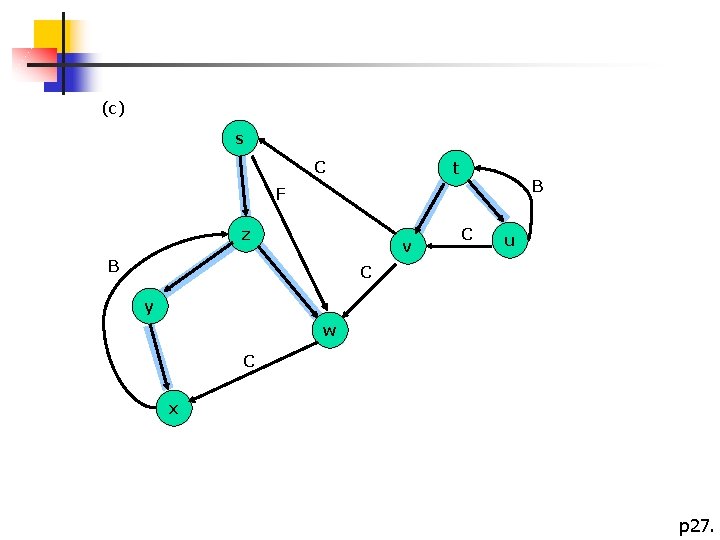
(c) s C t B F z v B C u C y w C x p 27.

n Thm 22. 7: (Parenthesis theorem) In any DFS of a graph G=( V, E ), for any two vertices u and v, exactly one of the following 3 conditions holds: (1). The intervals [u. d, u. f] and [v. d, v. f] are disjoint, (2). The interval [u. d, u. f] is contained entirely within the interval [v. d, v. f], and u is a descendant of v in the depth-first tree, (3). or as above with v as a descendant of u p 28.

Pf: 1. If u. d < v. d case 1: v. d < u. f : v was discovered while u was still gray. v is a descendant of u, and all v’s outgoing edges are explored So v is finished before finishing u. Thus (3) holds case 2: u. f < v. d u. d < u. f < v. d < v. f (1) holds 2. If v. d < u. d: Similarly, by switching the roles of u and v p 29.

n n Cor 8: v is a proper descendant of vertex u in the depth-first forest for a graph G iff u. d < v. f < u. f Thm 9: (White-path theorem) In a DF forest of G=( V, E ), vertex v is a descendant of u iff at the time u. d that the search discovers u, v can be reached from u along a path consisting entirely of white vertices p 30.

n Pf: “ ” v: descendant of u u w u. d < w. d, by the above cor. v Thus w is white at time u. d “ ” Assume at time u. d, v is reachable from u along a path of white vertices, but v does not become a descendant of u in DF tree w u v Descendant of u w. f <= u. f v must be discovered after u is discovered, but before w is finished. Thus, u. d < v. d < w. f <= u. f Thm 7 implies [v. d, v. f] is contained entirely in [u. d, u. f] By Cor 8, v is a descendant of u. p 31.

n Thm 22. 10: In a DFS of an undirected graph G, every edge of G is either a tree edge or a back edge Pf: Let and suppose u. d < v. d. Then v must be discovered and finished before finishing u n n If (u, v) is explored first in the direction from u to v, then (u, v) becomes a tree edge If (u, v) is explored first in the direction from v to u, then (u, v) is a back edge, since u is still gray at the time (u, v) is first explored p 32.

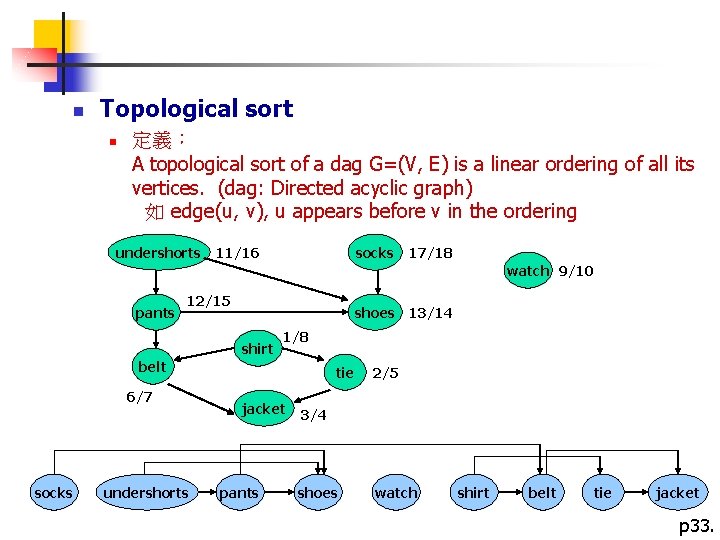
n Topological sort n 定義： A topological sort of a dag G=(V, E) is a linear ordering of all its vertices. (dag: Directed acyclic graph) 如 edge(u, v), u appears before v in the ordering undershorts socks 11/16 17/18 watch 9/10 pants 12/15 shoes shirt 1/8 belt 6/7 socks undershorts tie jacket pants 13/14 2/5 3/4 shoes watch shirt belt tie jacket p 33.

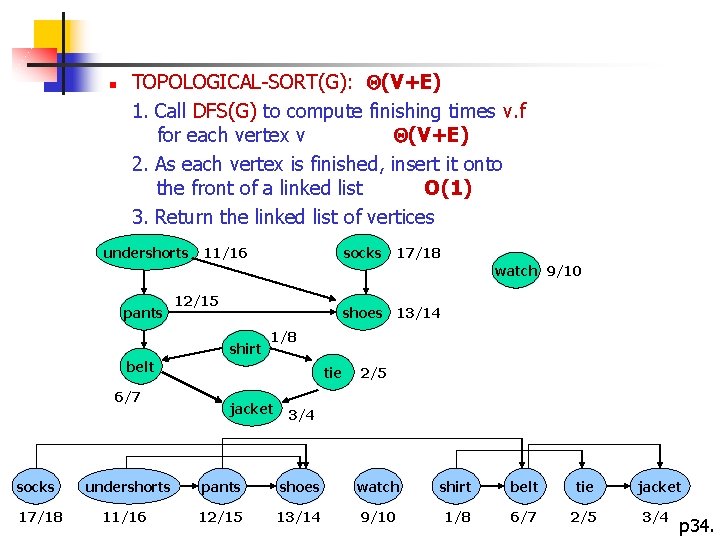
n TOPOLOGICAL-SORT(G): (V+E) 1. Call DFS(G) to compute finishing times v. f for each vertex v (V+E) 2. As each vertex is finished, insert it onto the front of a linked list O(1) 3. Return the linked list of vertices undershorts socks 11/16 17/18 watch 9/10 pants 12/15 shoes shirt 1/8 belt 6/7 socks 17/18 13/14 tie jacket 2/5 3/4 undershorts pants shoes watch shirt belt tie jacket 11/16 12/15 13/14 9/10 1/8 6/7 2/5 3/4 p 34.

Lemma 22. 11 A directed graph G is acyclic iff DFS(G) yields no back edges. pf: Suppose there is a back edge (u, v), v is an ancestor of u. Thus there is a path from v to u and a cycle exists. Suppose G has a cycle c. We show DFS(G) yields a back edge. n Let v be the first vertex to be discovered in c, and (u, v) be the preceding edge in c. n At time v. d, there is a path of white vertices from v to u. n By the white-path thm. , u becomes a descendant of v in the DF forest (u, v) is a back edge. n p 35.

n n n Thm 22. 12 TOPOLOGICAL-SORT(G) produces a topological sort of G pf: Suppose DFS is run to determine finishing times for vertices. It suffices to show that for any pair of u, v , if there is an edge from u to v, then v. f< u. f. When (u, v) is explored by DFS(G), v cannot be gray. Therefore v must be either white or black. 1. If v is white, it becomes a descendant of u, so v. f < u. f 2. If v is black, then v. f < u. f p 36.

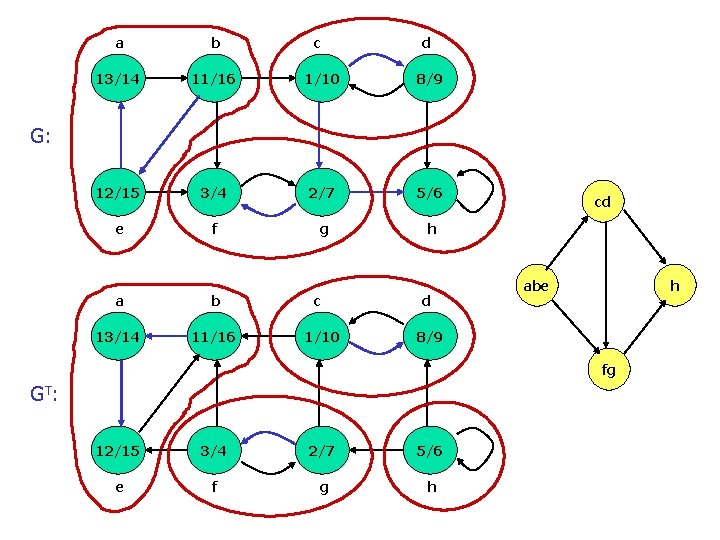
n Strongly connected components: n n n A strongly connected component of a directed graph G(V, E) is a maximal set of vertices U V s. t. for every pair u, v U, u and v are reachable from each other. Given G=(V, E), define GT=(V, ET), where ET={(u, v): (v, u) E} Given a G with adjacency-list representation, it takes O(V+E) to create GT. G and GT have the same strongly connected components. p 37.

a b c d 13/14 11/16 1/10 8/9 12/15 3/4 2/7 5/6 e f g h G: a b c d 13/14 11/16 1/10 8/9 cd abe h fg GT : 12/15 3/4 2/7 5/6 e f g h

n n Strongly. Connected. Components(G) 1. Call DFS(G) to compute finishing times u. f for each vertex u 2. Compute GT 3. Call DFS(GT), but in the main loop of DFS, consider the vertices in order of decreasing u. f 4. Output the vertices of each tree in the depth-first forest of step 3 as a separate strongly connected component Time: (V+E) p 39.

n Lemma 22. 13: Let C and C’ be distinct strongly connected components in directed graph G=(V, E), let u, v in C and u’, v’ in C’, and suppose there is a path from u to u’ in in G. Then there cannot also be a path from v’ to v in G. Def: Let U V, then we define d(U) = min { u. d } u U f (U) = max { u. f } u U p 40.

Lemma 22. 14 Let C and C’ be distinct strongly connected components in directed graph G=(V, E). Suppose that there is an edge (u, v) in E, where u in C and v in C’. Then f (C) > f ( C’). pf: (1) If d(C) < d(C’): let x be the 1 st discovered vertex in C. At time x. d all vertices in C and C’ are white. There is a path from x to all (white) vertices in C and to all vertices in C’: x~↝ u v ~↝ w. All vertices in C and C’ are descendants of x. Thus x. f = f (C) > f(C’). n (2) If d(C) > d(C’): let y be the 1 st discovered vertex in C’. At time y. d all vertices in C’ are white and there is a path from y to all vertices in C’. I. e. all vertices in C’ are descendants of y. So y. f = f(C’). There cannot be a path from C’ to C. Thus any w in C has w. f > y. f and so f(C) > f(C’). p 41.

Corollary 22. 15: Let C and C’ be distinct strongly connected components in directed graph G=(V, E). Suppose that there is an edge (u, v) in , where u in C and v in C’. Then f ( C ) < f ( C’ ). Pf: It is clear that (v, u) is in E. By the previous lemma we have f( C’ ) > f ( C ). p 42.

n n Thm 22. 16 Strongly-Connected-Component(G) correctly computes the strongly connected components of a directed graph. pf: By induction on the number (k) of depth-first trees found in the DFS of GT, where each tree forms a strongly connected component. Basis: trivial for k=0. Inductive step: assume each of the first k DFS trees produced in line 3 is a SCC. Consider the (k+1)-st tree produced. Let u be the root of this tree and let u be in SCC C. Thus u. f = f ( C ) > f ( C’ ) for any other SCC C’ yet to be visited. Note we visit in decreasing finishing time. p 43.

n n All other vertices in C are descendant of u in its DFS. By inductive hypothesis and the previous Corollary 15 any edges in GT that leave C must be to SCC’s already visited. Thus, no vertex in any SCC other than C will be a descendant of u during the DFS of GT. Thus, the vertices of the DFS tree in GT that is rooted at u form exactly one SCC. p 44.