Elementary Graph Algorithms Representations of graphs undirected graph

![Adjacency-array • 可藉由Adjacency-array表示,利用一個二維陣列A 存,若(u, v)是一個邊則A[u][v]=1反之A[u][v]=0。 1 2 3 4 5 1 0 0 1 Adjacency-array • 可藉由Adjacency-array表示,利用一個二維陣列A 存,若(u, v)是一個邊則A[u][v]=1反之A[u][v]=0。 1 2 3 4 5 1 0 0 1](https://slidetodoc.com/presentation_image_h/d73c58af7c8e222deb92ede7ea04f5d4/image-7.jpg)
























- Slides: 45

Elementary Graph Algorithms

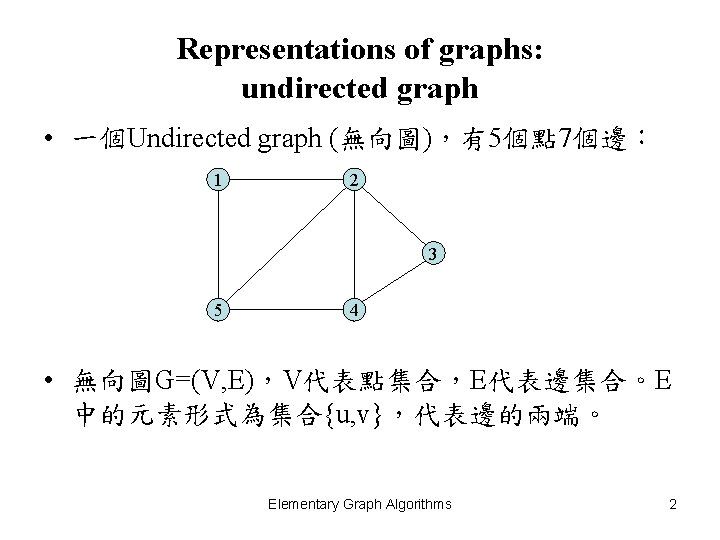
Representations of graphs: undirected graph • 一個Undirected graph (無向圖),有5個點 7個邊: 1 2 3 5 4 • 無向圖G=(V, E),V代表點集合,E代表邊集合。E 中的元素形式為集合{u, v},代表邊的兩端。 Elementary Graph Algorithms 2

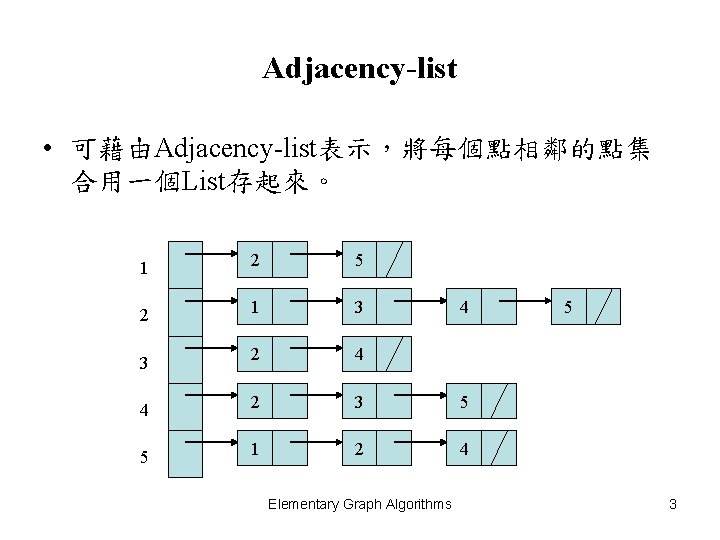
Adjacency-list • 可藉由Adjacency-list表示,將每個點相鄰的點集 合用一個List存起來。 1 2 5 2 1 3 3 2 4 4 2 3 5 5 1 2 4 Elementary Graph Algorithms 4 5 3

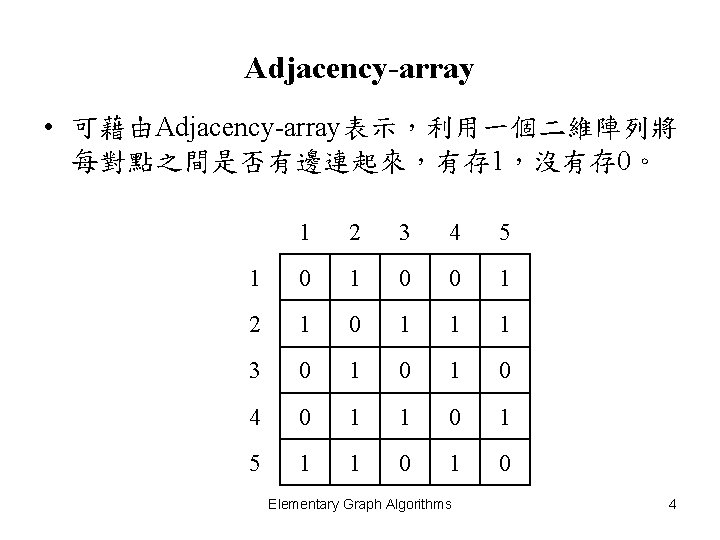
Adjacency-array • 可藉由Adjacency-array表示,利用一個二維陣列將 每對點之間是否有邊連起來,有存 1,沒有存 0。 1 2 3 4 5 1 0 0 1 2 1 0 1 1 1 3 0 1 0 4 0 1 1 0 1 5 1 1 0 Elementary Graph Algorithms 4

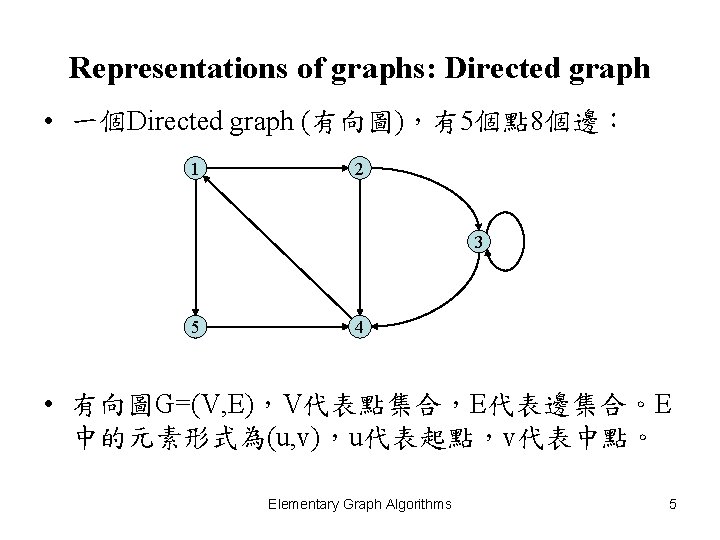
Representations of graphs: Directed graph • 一個Directed graph (有向圖),有5個點 8個邊: 1 2 3 5 4 • 有向圖G=(V, E),V代表點集合,E代表邊集合。E 中的元素形式為(u, v),u代表起點,v代表中點。 Elementary Graph Algorithms 5

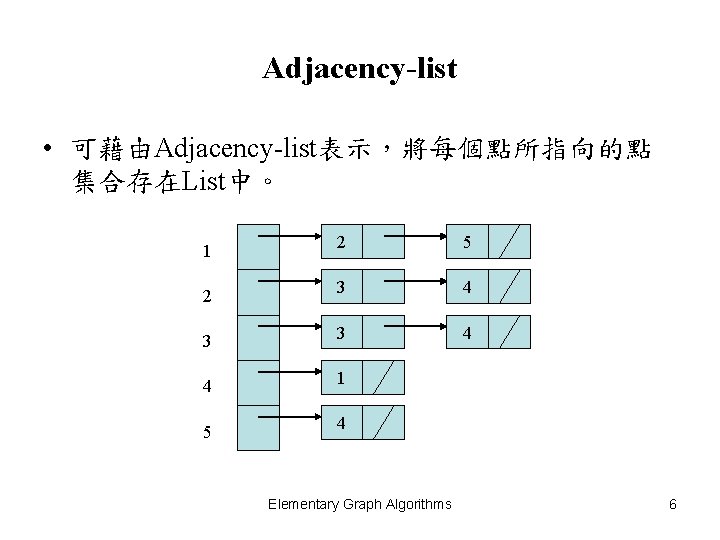
Adjacency-list • 可藉由Adjacency-list表示,將每個點所指向的點 集合存在List中。 1 2 5 2 3 4 3 3 4 4 1 5 4 Elementary Graph Algorithms 6
![Adjacencyarray 可藉由Adjacencyarray表示利用一個二維陣列A 存若u v是一個邊則Auv1反之Auv0 1 2 3 4 5 1 0 0 1 Adjacency-array • 可藉由Adjacency-array表示,利用一個二維陣列A 存,若(u, v)是一個邊則A[u][v]=1反之A[u][v]=0。 1 2 3 4 5 1 0 0 1](https://slidetodoc.com/presentation_image_h/d73c58af7c8e222deb92ede7ea04f5d4/image-7.jpg)
Adjacency-array • 可藉由Adjacency-array表示,利用一個二維陣列A 存,若(u, v)是一個邊則A[u][v]=1反之A[u][v]=0。 1 2 3 4 5 1 0 0 1 2 0 0 1 1 0 3 0 0 1 1 0 4 1 0 0 0 0 1 0 5 Elementary Graph Algorithms 7


Breadth-first search • BFS是許多重要的圖形演算法的原型,如 Prim’s minimum spanning tree演算法以及Dijkstra’s singlesource shortest-path演算法。 Elementary Graph Algorithms 9

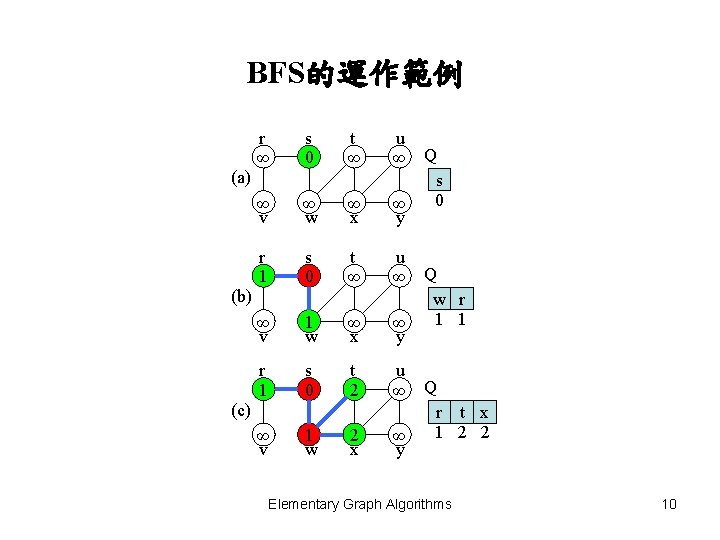
BFS的運作範例 r ∞ s 0 t ∞ ∞ v ∞ w ∞ x r 1 s 0 t ∞ ∞ v 1 w ∞ x r 1 s 0 t 2 ∞ v 1 w 2 x (a) (b) (c) u ∞ Q s 0 ∞ y u ∞ Q w r 1 1 ∞ y u ∞ Q r t x 1 2 2 ∞ y Elementary Graph Algorithms 10

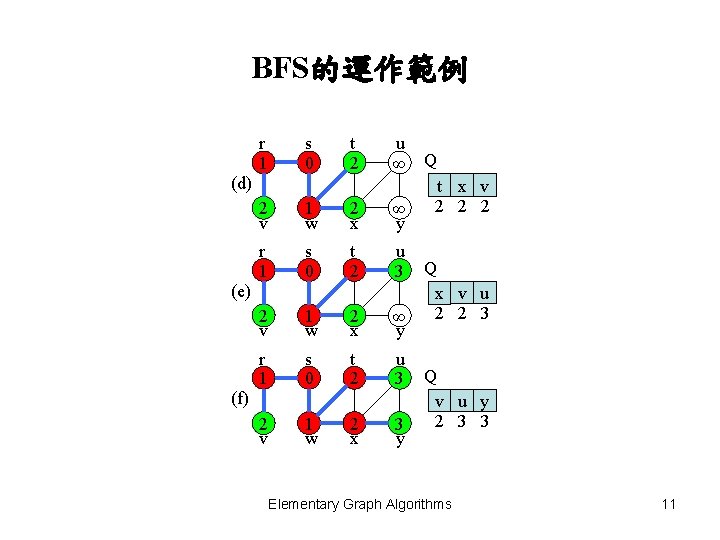
BFS的運作範例 r 1 s 0 t 2 u ∞ Q (d) t x v 2 2 v 1 w 2 x ∞ y r 1 s 0 t 2 u 3 2 v 1 w 2 x Q x v u 2 2 3 ∞ y r 1 s 0 t 2 u 3 2 v 1 w 2 x 3 y (e) (f) Q v u y 2 3 3 Elementary Graph Algorithms 11

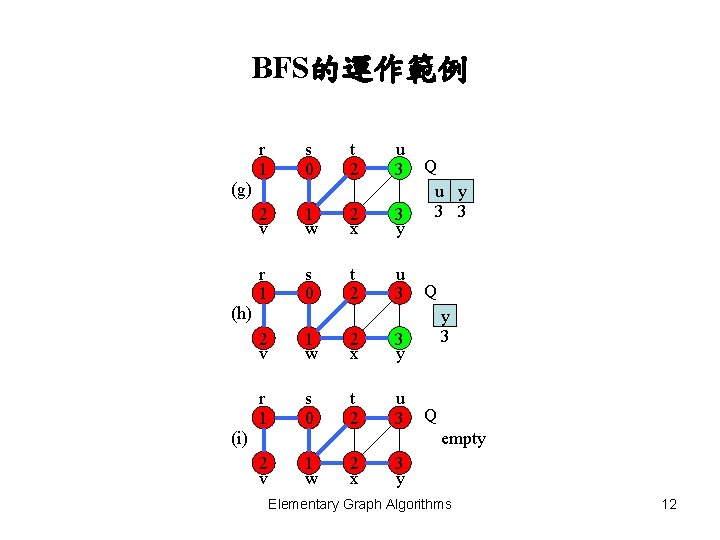
BFS的運作範例 r 1 s 0 t 2 u 3 2 v 1 w 2 x 3 y r 1 s 0 t 2 u 3 (g) Q u y 3 3 Q (h) 2 v 1 w 2 x 3 y r 1 s 0 t 2 u 3 (i) y 3 Q empty 2 v 1 w 2 x 3 y Elementary Graph Algorithms 12


BFS(G, s) 1. for each vertex u∈ G. V-{s} 2. u. color = WHITE 3. u. d = ∞ 4. u. π = NIL 5. s. color = GREEN 6. s. d = 0 7. s. π = NIL 8. Q = empty 9. Enqueue(Q, s) 10. while Q≠empty 11. u = Dequeue(Q) 12. for each v∈ G. Adj[u] 13. if v. color == WHITE 14. v. color = GREEN 15. v. d = u. d + 1 16. v. π = u 17. Enqueue(Q, v) 18. u. color = RED Time Complexity: O(|E|+|V|) Elementary Graph Algorithms 14


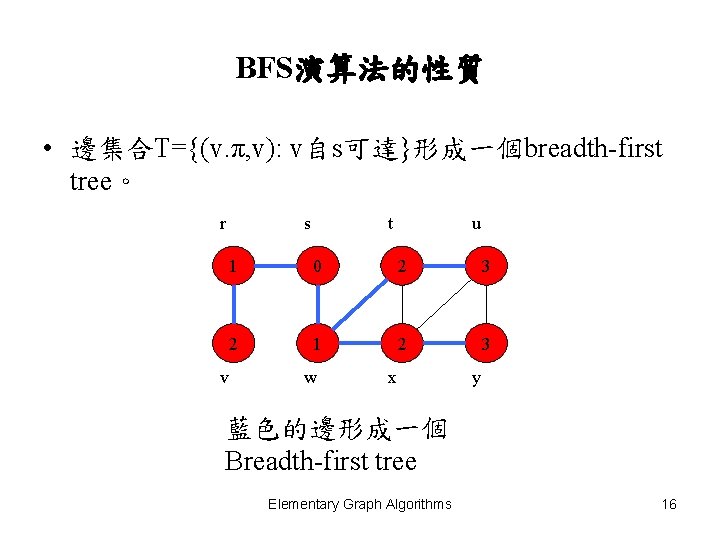
BFS演算法的性質 • 邊集合T={(v. π, v): v自s可達}形成一個breadth-first tree。 r v s t u 1 0 2 3 2 1 2 3 w x y 藍色的邊形成一個 Breadth-first tree Elementary Graph Algorithms 16

Print path演算法 • 可在執行過BFS演算法的圖上印出s到v的最短路 徑。如無路徑也會印出沒有路徑的訊息。 Print-Path(G, s, v) 1. if v == s 2. print s 3. elseif v. π== NIL 4. print “no path from” s “to” v 5. else Print-Path(G, s, v. π) 6. print v Elementary Graph Algorithms 17



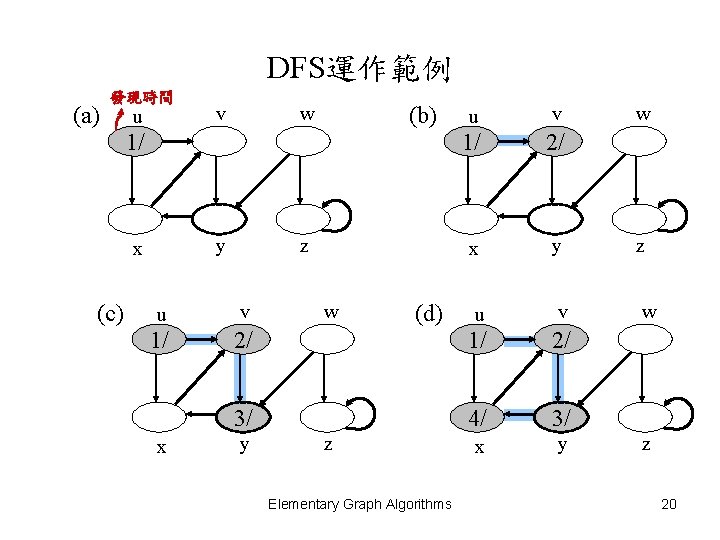
DFS運作範例 (a) 發現時間 u v (b) w 1/ y x (c) z (d) v 1/ 2/ x y z u v w u v 1/ 2/ 3/ 4/ 3/ x y w u z Elementary Graph Algorithms w z 20

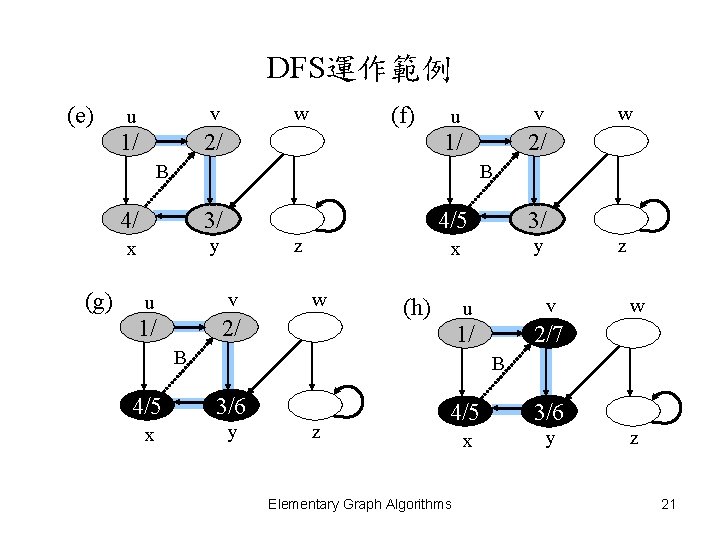
DFS運作範例 (e) u v 1/ 2/ (f) w u v 1/ 2/ B (g) w B 4/ 3/ x y z u v 1/ 2/ w 4/5 3/ x y (h) B z u v 1/ 2/7 w B 4/5 3/6 x y z 4/5 3/6 x y Elementary Graph Algorithms z 21

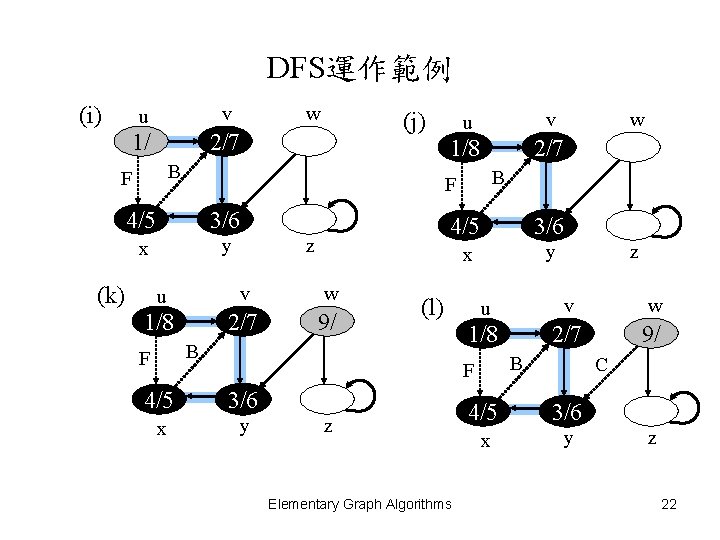
DFS運作範例 (i) u v w 1/ 2/7 (j) B F v 1/8 2/7 3/6 x y z u v w 1/8 2/7 9/ 4/5 3/6 x y (l) B F 3/6 x y z Elementary Graph Algorithms z u v w 1/8 2/7 9/ B F 4/5 w B F 4/5 (k) u C 4/5 3/6 x y z 22

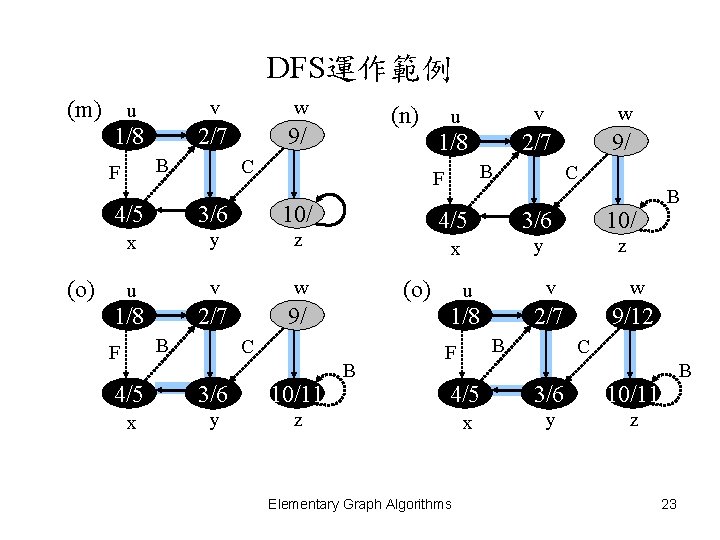
DFS運作範例 (m) u v w 1/8 2/7 9/ B F C 3/6 10/ x y z u v w 1/8 2/7 9/ B F 4/5 (o) (n) 4/5 3/6 10/11 x y z 4/5 3/6 10/ x y z (o) C B C u v w 1/8 2/7 9/12 B F C 4/5 3/6 10/11 x y z Elementary Graph Algorithms B B 23

DFS演算法 DFS(G) 1. for each vertex u∈ G. V 2. do u. color = WHITE 3. u. π = NIL 4. time = 0 5. for each vertex u ∈ G. V 6. if u. color == WHITE 7. DFS-Visit(G, u) Elementary Graph Algorithms 24

DFS-Visit演算法 DFS-Visit(G, u) 1. time = time+1 //u has just been discovered 2. u. d = time 3. u. color = GRAY 4. for each v ∈ G. Adj[u] 5. if v. color == WHITE 6. v. π = u 7. DFS-Visit(G, v) 8. u. color = BLACK //DFS-Visit(G, u) is done 9. time = time + 1 10. u. f = time Elementary Graph Algorithms 25


邊的分類 • 假定邊為(u, v) • Tree edges: 若初次發現v時是藉由(u, v),即v. π=u, 則此邊稱作tree edge。 • Back edges: 若v是u的ancestor,則此邊稱作back edge。 • Forward edges: 若v是u的descendant且(u, v)不是tree edge,則此邊稱作forward edge。 • Cross edges: 不屬於前三類的邊均稱為Cross edges。 Elementary Graph Algorithms 27

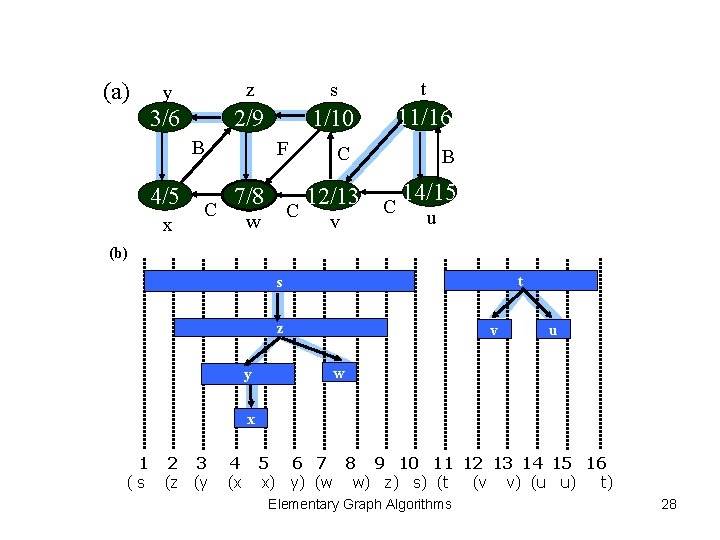
(a) y z s t 3/6 2/9 1/10 11/16 C B B 4/5 x C F 12/13 C 14/15 C u 7/8 w v (b) t s z y v u w x 1 (s 2 3 (z (y 4 (x 5 6 7 8 9 10 11 12 13 14 15 16 x) y) (w w) z) s) (t (v v) (u u) t) Elementary Graph Algorithms 28

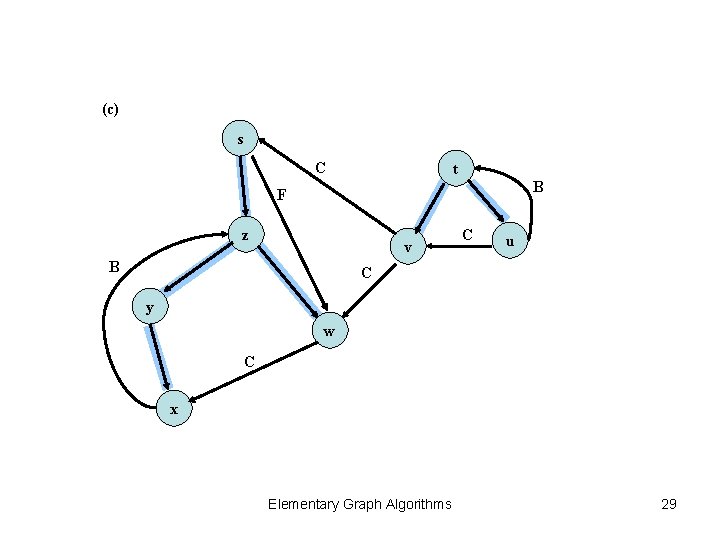
(c) s C t B F z v B C u C y w C x Elementary Graph Algorithms 29

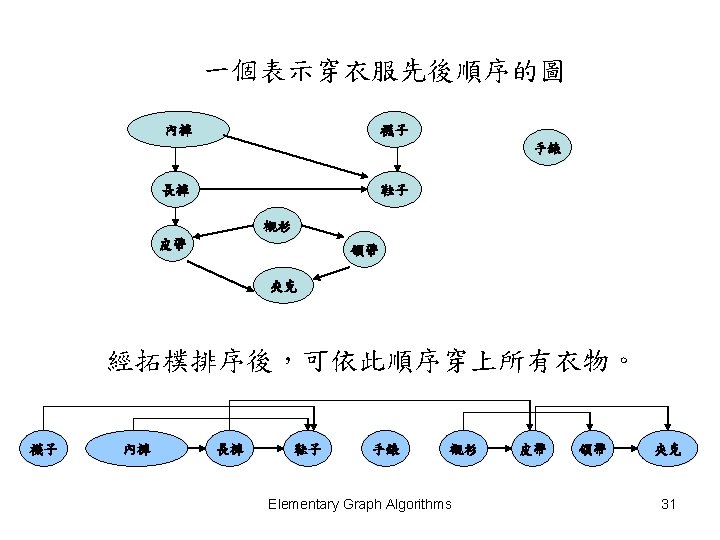
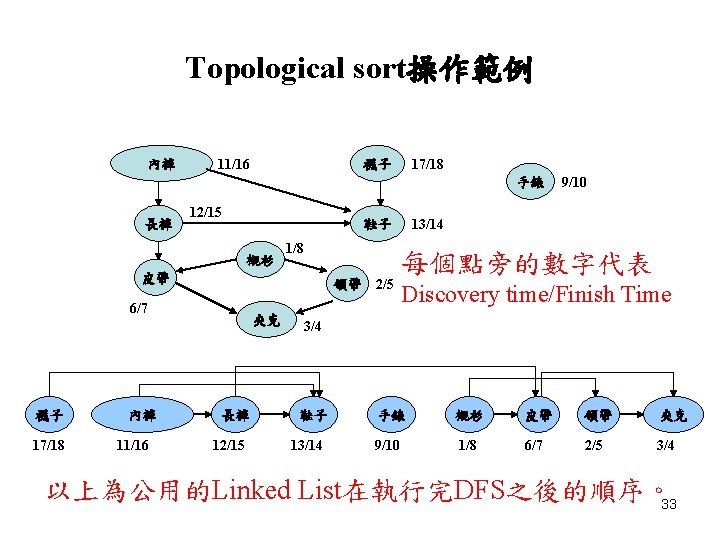
Topological sort • 對一DAG (Directed acyclic graph,有向無迴圈圖) G=(V, E),Topological sort(拓樸排序)是一對V的排 序,其中若(u, v) ∈ E則在排序中u必須排在v之前。 • 常用於決定排程。 Elementary Graph Algorithms 30


Topological sort演算法 • 利用DFS演算法,計算出每一個點u的Finish time (u. f)。 • 當一個點執行完畢DFS-Visit時,將該點放入一公 用的Linked List前端。 • 最後此Linked List存放的順序即為一Topological sort。 Elementary Graph Algorithms 32


Lemma 22. 11: A directed graph G is acyclic iff DFS(G) yields no back edges. Pf: Suppose there is a back edge (u, v), v is an ancestor of u. Thus there is a path from v to u and a cycle exists. n Suppose G has a cycle c. We show DFS(G) yields a back edge. Let v be the first vertex to be discovered in c, and (u, v) be the preceding edge in c. At time v. d, there is a path of white vertices from v to u. By the white-path thm. , u becomes a descendant of v in the DF forest. Thus (u, v)is a back edge. Elementary Graph Algorithms 34

Thm 22. 12 TOPOLOGICAL-SORT(G) produces a topological sort of G pf: l Suppose DFS is run to determinate finishing times for vertices. l It suffices to show that for any pair of u, v , if there is an edge from u to v, then v. f < u. f. l When (u, v) is explored by DFS(G), v cannot be gray. l Therefore v must be either white or black. 1. If v is white, it becomes a descendant of u, so v. f<u. f 2. If v is black, then v. f<u. f Elementary Graph Algorithms 35

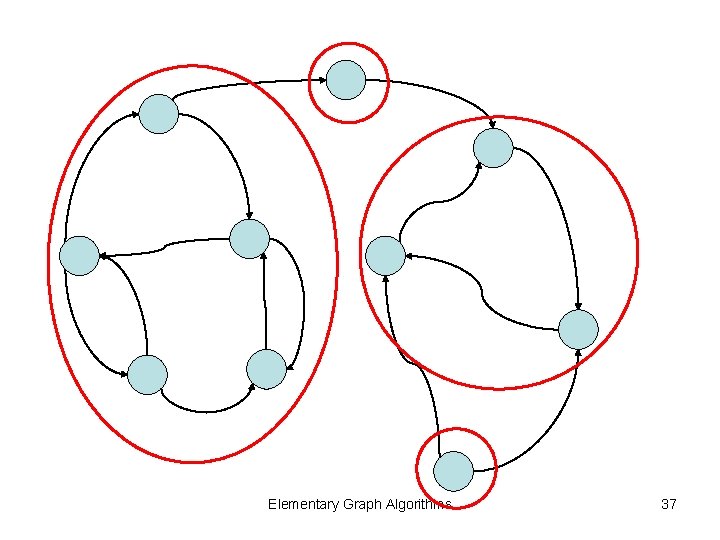
Strongly connected components • 對一個有向圖G=(V, E)而言,一個Strongly Connected Component C是一個滿足下列條件的點 集合: – C⊆ V – 對任C中相異兩點u及v,存在一條路徑由u到v 且有另一路徑由v到u。 Elementary Graph Algorithms 36

Elementary Graph Algorithms 37

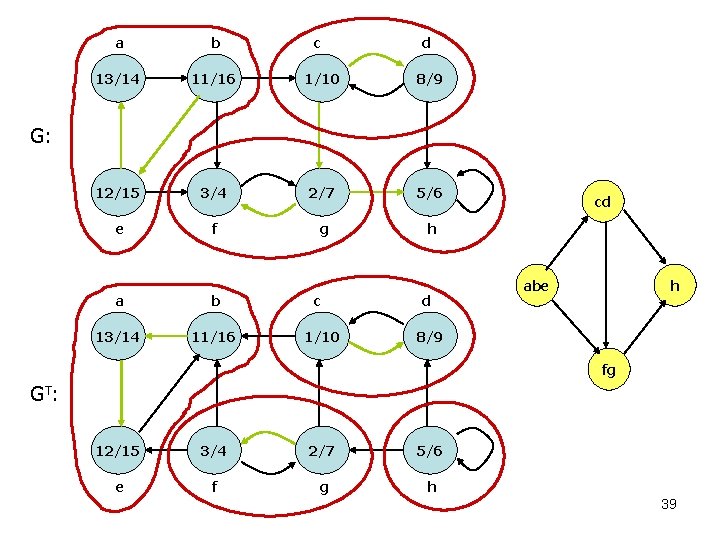
Strongly connected components演算法 1. 呼叫DFS(G)對所有點u,計算出u. f,即finishing time。 2. 計算出GT,即點集合與G相同,而邊連接方向相 反的圖。 3. 呼叫DFS(GT),但在DFS主迴圈中,選擇點的順 序是先挑取u. f值較大的點u。(即以u. f遞減順序挑 取。) 4. 在DFS(GT)的Depth-first forest中,每一個樹均是 一個Strongly connected component。 Elementary Graph Algorithms 38

a b c d 13/14 11/16 1/10 8/9 12/15 3/4 2/7 5/6 e f g h G: a b c d 13/14 11/16 1/10 8/9 cd abe h fg GT : 12/15 3/4 2/7 5/6 e f g h 39

Lemma 22. 13 : Let C and C’ be distinct strongly connected components in directed graph G=(V, E), let u, v in C and u’, v’ in C’, and suppose there is a path from u to u’ in G. Then there cannot also be a path from v’ to v in G. Def: Let U V, define d(U) = min u U { u. d } f (U) = max u U { u. f } Elementary Graph Algorithms 40

Lemma 22. 14 Let C and C’ be distinct strongly connected components in directed graph G=(V, E). Suppose that there is an edge (u, v) in E, where u in C and v in C’. Then f (C) > f ( C’). pf: Case (1): l If d(C) < d(C’): let x be the 1 st discovered vertex in C. l At time x. d all vertices in C and C’ are white. l There is a path from x to all (white) vertices in C and to all vertices in C’: x~↝ u v ~↝ w. l All vertices in C and C’ are descendants of x. Thus x. f = f (C) > f(C’). Elementary Graph Algorithms 41

Lemma 22. 14 Let C and C’ be distinct strongly connected components in directed graph G=(V, E). Suppose that there is an edge (u, v) in E, where u in C and v in C’. Then f (C) > f ( C’). pf: Case (2): l If d(C) > d(C’): let y be the 1 st discovered vertex in C’. l At time y. d all vertices in C’ are white and there is a path from y to all vertices in C’. l I. e. all vertices in C’ are descendants of y. l So y. f = f(C’). There cannot be a path from C’ to C. Why? l Thus any w in C has w. f > y. f and so f(C) > f(C’). Elementary Graph Algorithms 42

Corollary 22. 15: Let C and C’ be distinct strongly connected components in directed graph G=(V, E). Suppose that there is an edge (u, v) in ET, where u in C and v in C’. Then f ( C ) < f ( C’ ). Pf: It is clear that (v, u) is in E. By the previous lemma we have f( C’ ) > f ( C ). Elementary Graph Algorithms 43

Theorem 22. 16 Strongly-Connected-Component(G) correctly computes the strongly connected components of a directed graph. pf: l By induction on the number (k) of depth-first trees found in the DFS of GT, where each tree forms a strongly connected component. l Basis: trivial for k=0. l Inductive step: assume each of the first k DFS trees produced in line 3 is a SCC. l Consider the (k+1)-st tree produced. Let u be the root of this tree and let u be in SCC C. l Thus u. f = f ( C ) > f ( C’ ) for any other SCC C’ yet to be visited. Note we visit in decreasing finishing time. Elementary Graph Algorithms 44

l All other vertices in C are descendant of u in its DFS. l By inductive hypothesis and the Corollary 15 any edges in GT that leave C must be to SCC’s already visited. l Thus, no vertex in any SCC other than C will be a descendant of u during the DFS of GT. l Thus, the vertices of the DFS tree in GT that is rooted at u form exactly one SCC. Elementary Graph Algorithms 45