GEOSTATYSTYKA Wykad dla III roku Geografii specjalno geoinformacja

GEOSTATYSTYKA Wykład dla III roku Geografii specjalność - geoinformacja Alfred Stach Instytut Paleogeografii i Geoekologii Wydział Nauk Geograficznych i Geologicznych UAM

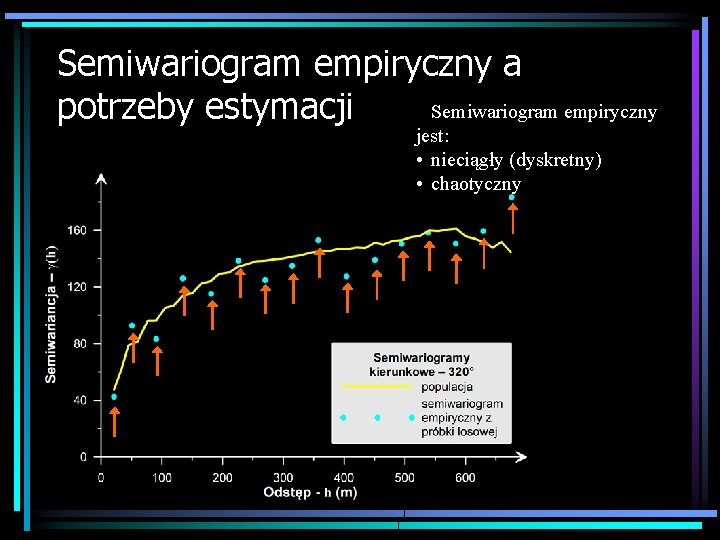
Semiwariogram empiryczny a Semiwariogram empiryczny potrzeby estymacji jest: • nieciągły (dyskretny) • chaotyczny

Kryterium połowicznej pozytywnej określoności (ang. positive semidefinite) • Estymowane lub symulowane wartości są w geostatystyce traktowane jako zmienne losowe będące liniową kombinacją innych znanych zmiennych losowych. • Wariancja zaś jakiejkolwiek liniowej kombinacji Y zmiennych losowych Z(u ), u A, jest wówczas liniową kombinacją wartości kowariancji owych zmiennych i musi nieujemna (ang. non-negative) dla jakiejkolwiek z wybranych n lokalizacji u A i dla jakiejkolwiek wagi • Spełnienie tego warunku jest możliwe tylko przy zastosowaniu takich funkcji kowariancji C(h), nieparametrycznych czy też parametrycznych, które są pozytywnie połowicznie określone.

Kryterium połowicznej pozytywnej określoności (ang. positive semidefinite) • Stosowanie interpolowanych / ekstrapolowanych wartości empirycznych miar struktury przestrzennej nigdy nie gwarantuje, że obliczenia estymacji / symulacji dadzą jakikolwiek wynik. • Gwarancję taką można mieć jedynie przy zastosowaniu modelu matematycznego o takiej postaci, który jest z góry pozytywnie połowicznie określony. • Modele takie określa się jako dozwolone (ang. permissible).

Model nuggetowy (losowy) Gaussowska symulacja bezwarunkowa dla zmiennej o średniej 0 i wariancji nuggetowej równej 10

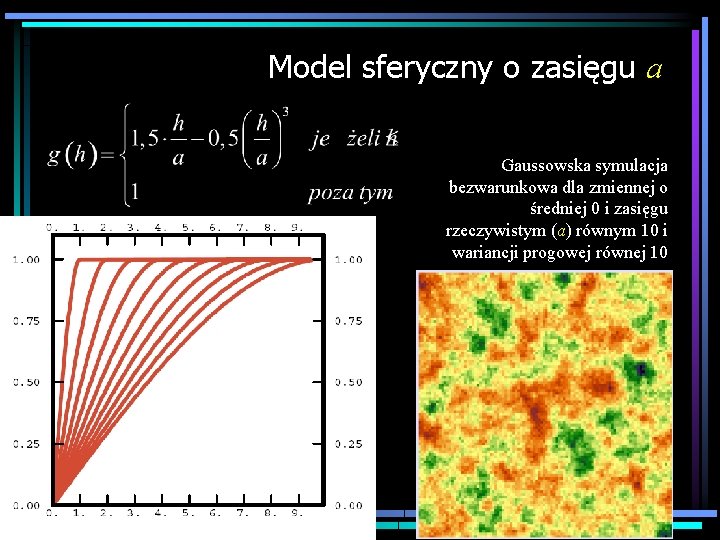
Model sferyczny o zasięgu a Gaussowska symulacja bezwarunkowa dla zmiennej o średniej 0 i zasięgu rzeczywistym (a) równym 10 i wariancji progowej równej 10

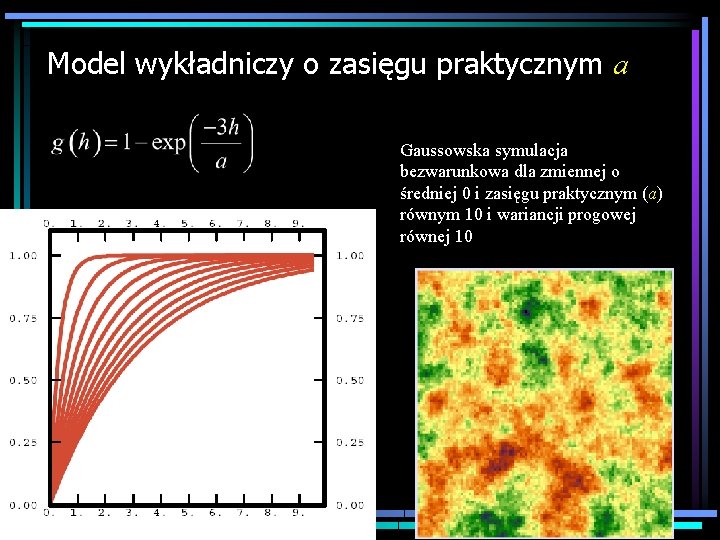
Model wykładniczy o zasięgu praktycznym a Gaussowska symulacja bezwarunkowa dla zmiennej o średniej 0 i zasięgu praktycznym (a) równym 10 i wariancji progowej równej 10

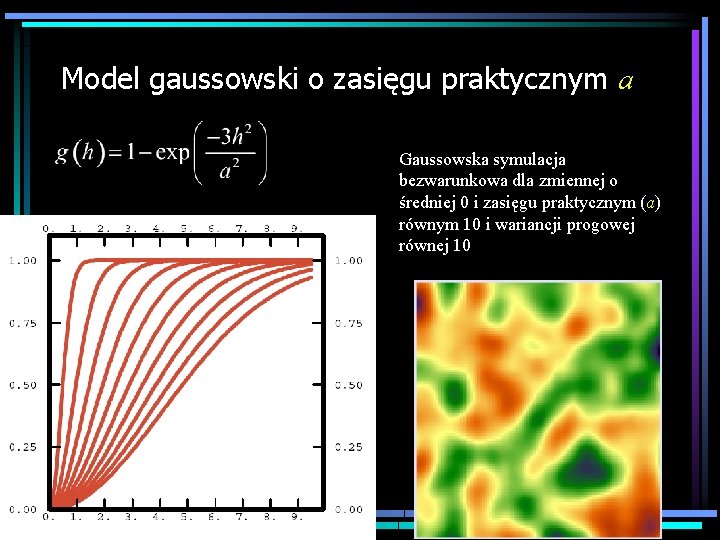
Model gaussowski o zasięgu praktycznym a Gaussowska symulacja bezwarunkowa dla zmiennej o średniej 0 i zasięgu praktycznym (a) równym 10 i wariancji progowej równej 10

Model liniowy z wariancją progową o zasięgu rzeczywistym a Gaussowska symulacja bezwarunkowa dla zmiennej o średniej 0 i zasięgu rzeczywistym (a) równym 10 i wariancji progowej równej 10

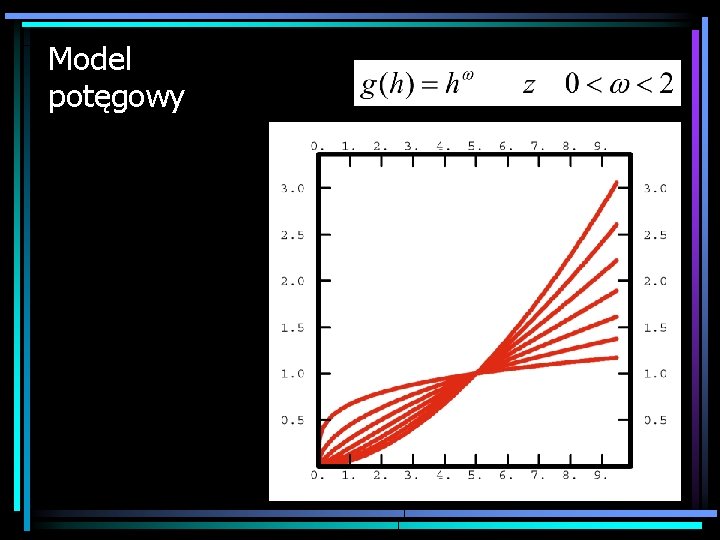
Model potęgowy

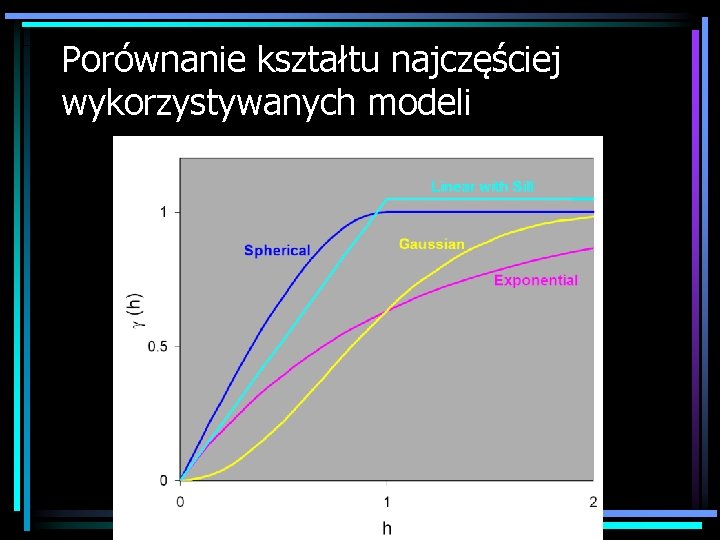
Porównanie kształtu najczęściej wykorzystywanych modeli

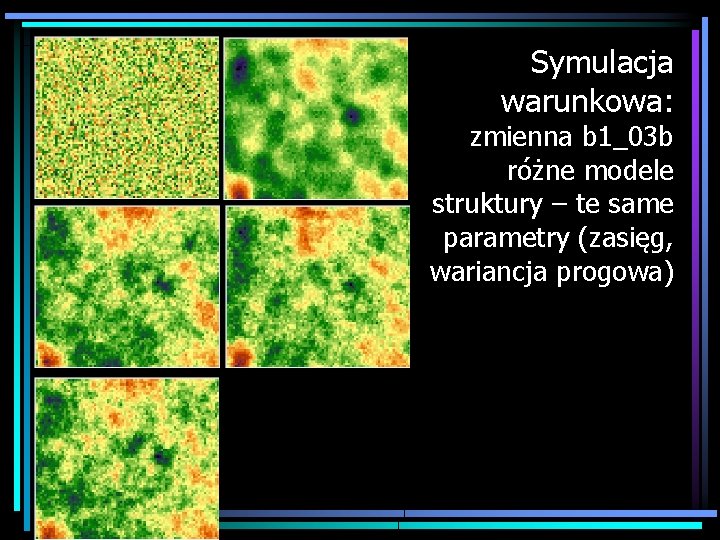
Symulacja warunkowa: zmienna b 1_03 b różne modele struktury – te same parametry (zasięg, wariancja progowa)

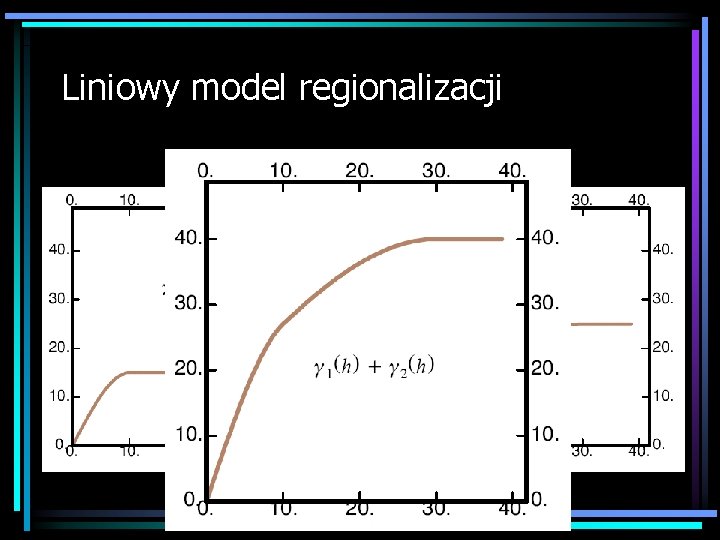
Liniowy model regionalizacji • W wielu sytuacjach, aby odwzorować dokładnie kształt semiwariogramu empirycznego konieczne jest połączenie dwóch, lub większej ilości modeli podstawowych g(h). • Nie wszystkie kombinacje dopuszczalnych modeli dają w efekcie funkcję dopuszczalną, to znaczy z nieujemną wariancją. • Najprostszym sposobem utworzenia modelu dopuszczalnego jest stworzenie najpierw funkcji losowej. Semiwariogram takiej funkcji jest z definicji dopuszczalny

Liniowy model regionalizacji • Praktycznie rzecz biorąc konieczne jest spełnienie dwóch warunków tak zwanego liniowego modelu regionalizacji (ang. linear regionalisation model): – – wszystkie użyte w modelu złożonym podstawowe funkcje gl(h) muszą być dopuszczalne, wariancja progowa bl każdego podstawowego modelu semiwariogramu musi być dodatnia, a wówczas: Model złożony (h) jest w takiej sytuacji wyrażony jako pozytywna liniowa kombinacja podstawowych modeli semiwariogramów gl(h). W literaturze przedmiotu popularna jest jego także alternatywna nazwa: „ nested model” czyli model zagnieżdżony.

Liniowy model regionalizacji

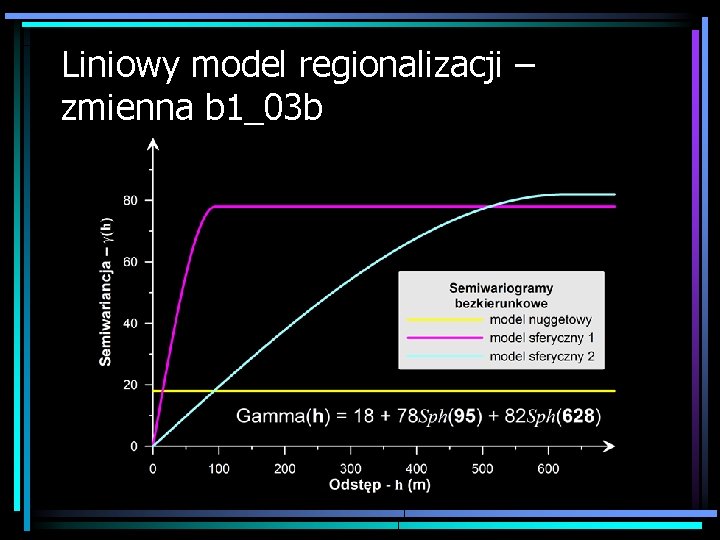
Liniowy model regionalizacji – zmienna b 1_03 b

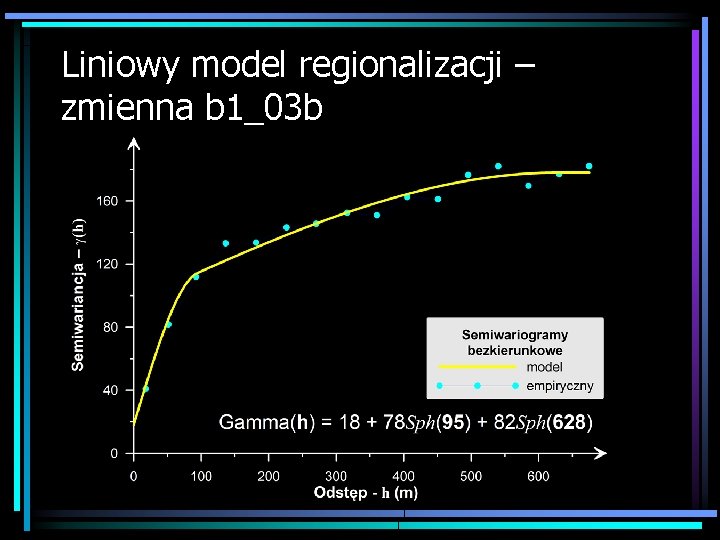
Liniowy model regionalizacji – zmienna b 1_03 b

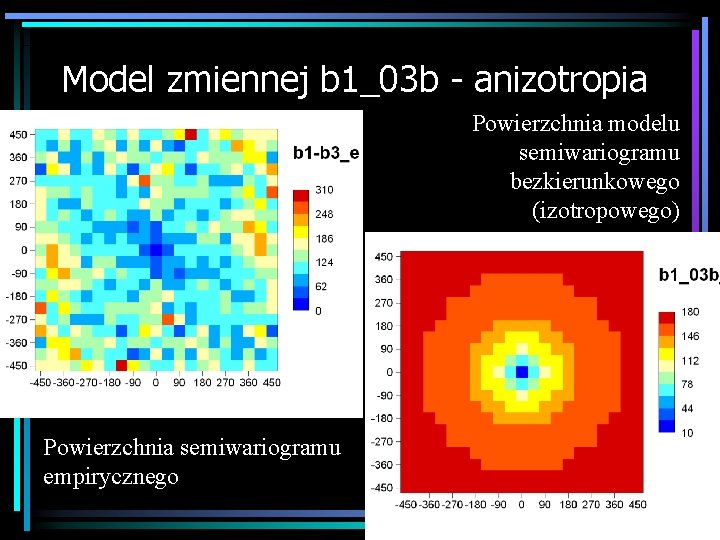
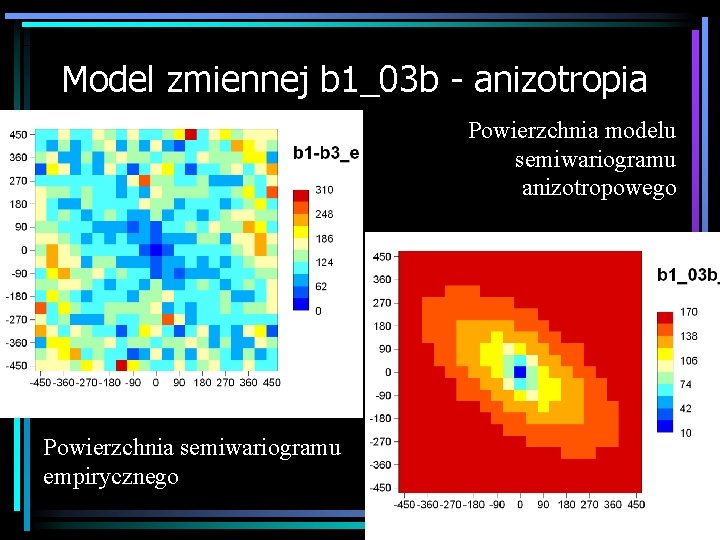
Model zmiennej b 1_03 b - anizotropia Powierzchnia modelu semiwariogramu bezkierunkowego (izotropowego) Powierzchnia semiwariogramu empirycznego

Model zmiennej b 1_03 b - anizotropia Powierzchnia modelu semiwariogramu anizotropowego Powierzchnia semiwariogramu empirycznego

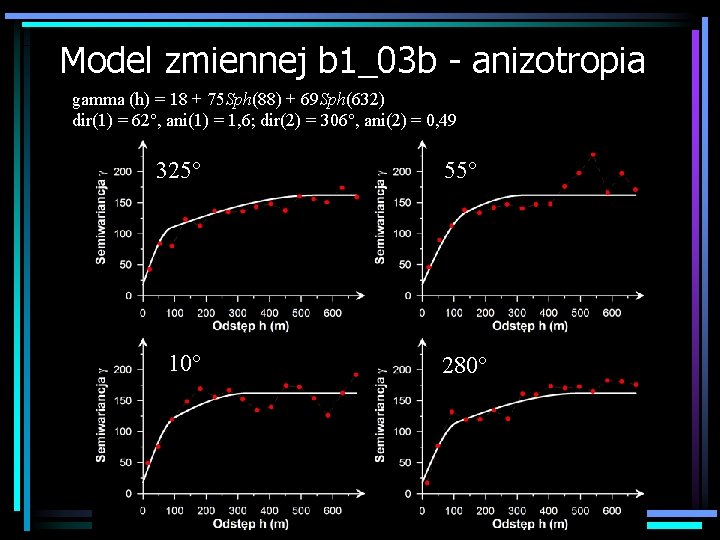
Model zmiennej b 1_03 b - anizotropia gamma (h) = 18 + 75 Sph(88) + 69 Sph(632) dir(1) = 62°, ani(1) = 1, 6; dir(2) = 306°, ani(2) = 0, 49 325° 55° 10° 280°

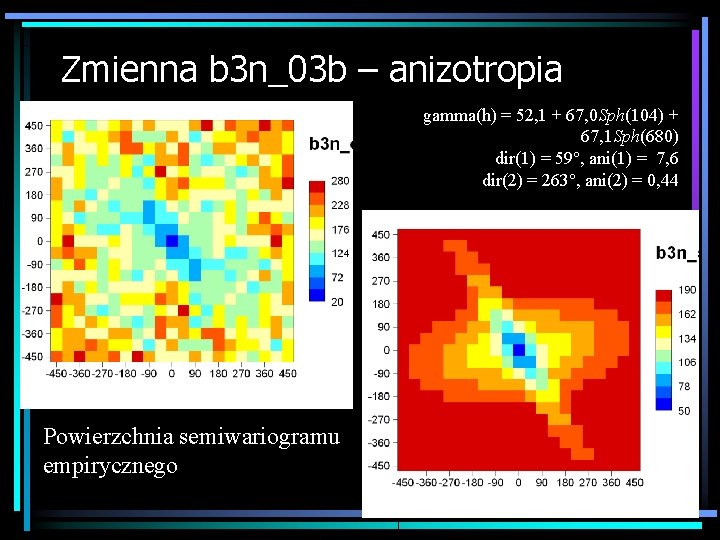
Zmienna b 3 n_03 b – anizotropia gamma(h) = 52, 1 + 67, 0 Sph(104) + 67, 1 Sph(680) dir(1) = 59°, ani(1) = 7, 6 dir(2) = 263°, ani(2) = 0, 44 Powierzchnia semiwariogramu empirycznego

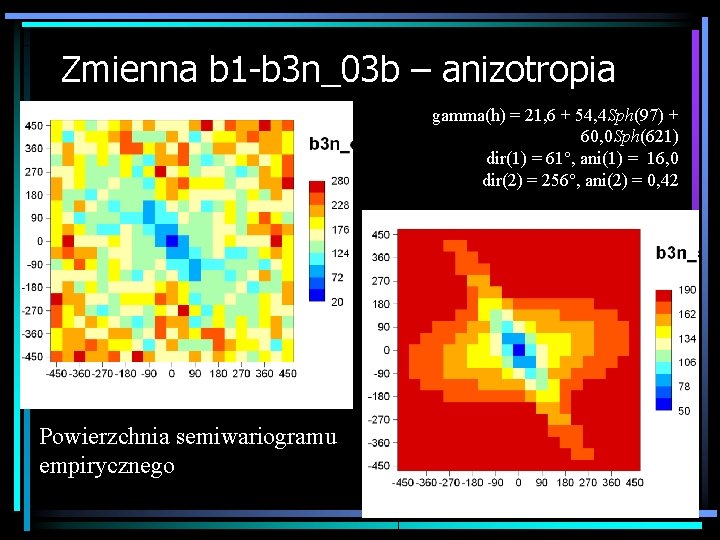
Zmienna b 1 -b 3 n_03 b – anizotropia gamma(h) = 21, 6 + 54, 4 Sph(97) + 60, 0 Sph(621) dir(1) = 61°, ani(1) = 16, 0 dir(2) = 256°, ani(2) = 0, 42 Powierzchnia semiwariogramu empirycznego

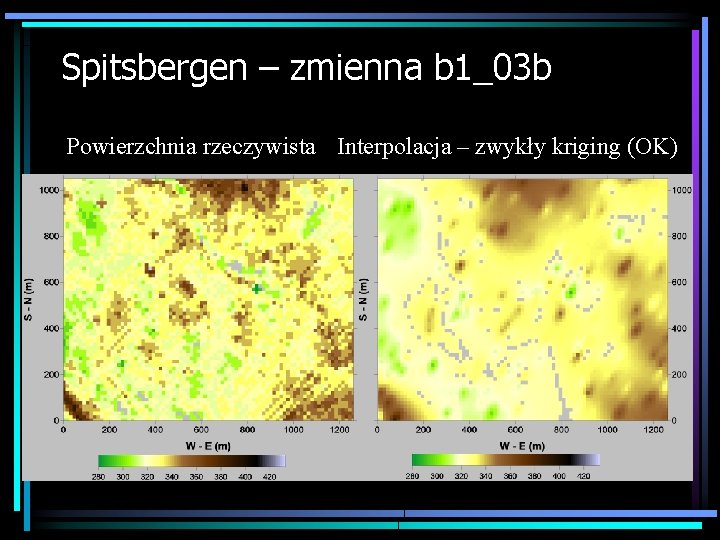
Spitsbergen – zmienna b 1_03 b Powierzchnia rzeczywista Interpolacja – zwykły kriging (OK)

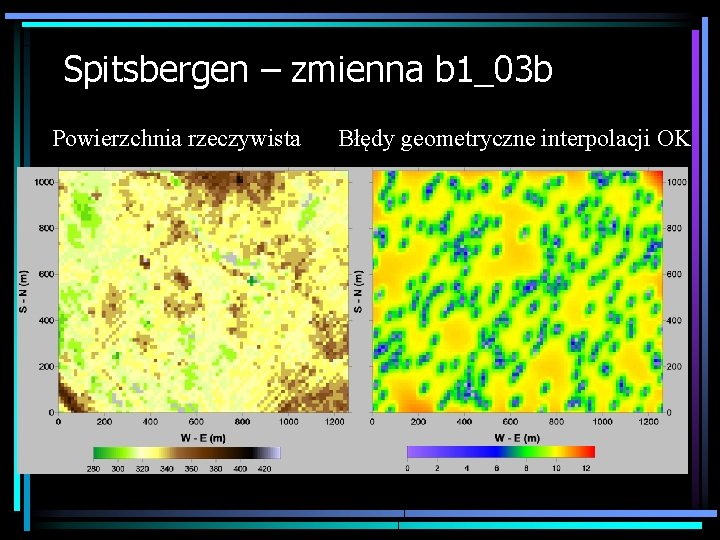
Spitsbergen – zmienna b 1_03 b Powierzchnia rzeczywista Błędy geometryczne interpolacji OK

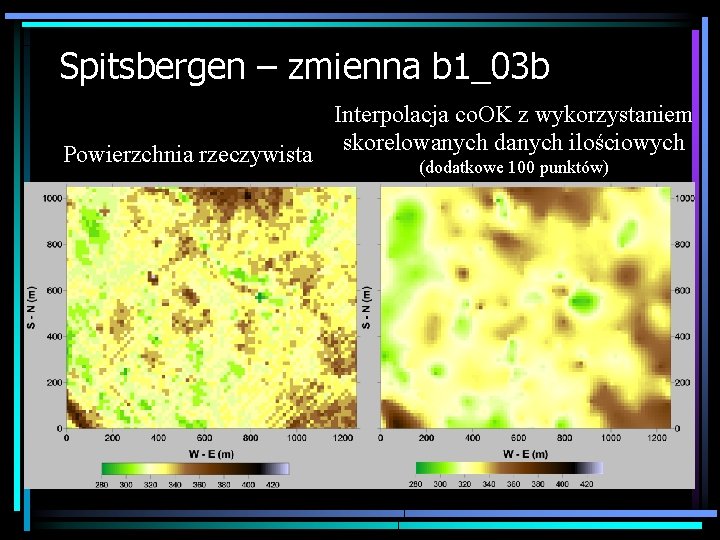
Spitsbergen – zmienna b 1_03 b Interpolacja co. OK z wykorzystaniem danych ilościowych Powierzchnia rzeczywista skorelowanych (dodatkowe 100 punktów)

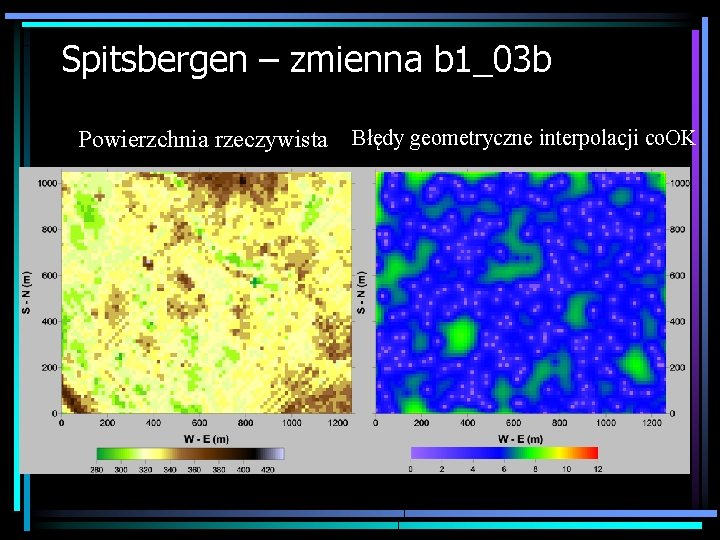
Spitsbergen – zmienna b 1_03 b Powierzchnia rzeczywista Błędy geometryczne interpolacji co. OK

Podstawowe zasady przed tworzeniem liniowego modelu koregionalizacji 1. Semiwariogramy i kros semiwariogramy empiryczne będące podstawą szacowania LCM muszą być obliczane dla tej samej ilości i wielkości odstępów i dla tych samych kierunków. 2. Sporządzenie LCM dla Nv cech wymaga jednoczesnego modelowania Nv (Nv+1)/2 semiwariogramów i kros semiwariogramów. 3. Najwyższą, decydującą wagę przy podejmowaniu decyzji o postaci LCM ma forma semiwariogramu zmiennej pierwotnej, czyli tej, która ma być estymowana.

Liniowy model koregionalizacji (LCM) LCM jest zdefiniowany jako zbiór Nv modeli semiwariogramów i kros semiwariogramów ij(h), takich że: gdzie każda funkcja gl(h) jest dopuszczalnym modelem semiwariogramu, i (L+1) macierzy współczynników stanowiących sill lub nachylenie modelu gl(h) są wszystkie połowicznie pozytywnie określone.

Kryterium połowicznej pozytywnej określoności macierzy (positive semi-definite) Symetryczna macierz jest połowicznie pozytywnie określona jeśli jej wyznacznik oraz wszystkie jej główne podwyznaczniki nie są ujemne. Przykładowy liniowy model koregionalizacji dla Nv=3: Każda macierz koregionalizacji Bl jest połowicznie określona pozytywnie jeśli spełnione jest następujących siedem nierównosci

Kryterium połowicznej pozytywnej określoności macierzy (positive semi-definite) • Wszystkie elementy przekątnej nie są negatywne: • Wszystkie główne podwyznaczniki stopnia 2 nie są negatywne:

Kryterium połowicznej pozytywnej określoności macierzy (positive semi-definite) • Wyznacznik stopnia 3 nie jest negatywny:

Pojęcie struktura oznacza: Podstawowe zasady w trakcie tworzeniem (a) typ modelu, (b) zasięg, liniowego modelu koregionalizacji (c) kierunek 1. Każda elementarna struktura pojawiająca się na kros semiwariogramie ij(h) musi istnieć w obu modelach semiwariogramów jednostkowych ii(h) i jj(h). 2. Jeśli elementarna struktura gl(h) nie występuje na semiwariogramie jednostkowym danej zmiennej, to musi być ona nieobecna także na wszystkich kros semiwariogramach zawierających ową zmienną.

Pojęcie struktura oznacza: Podstawowe zasady w trakcie tworzeniem (a) typ modelu, (b) zasięg, liniowego modelu koregionalizacji (c) kierunek 3. Każdy model jednostkowego czy też kros semiwariogramu ij(h) nie musi zawierać wszystkich (L + 1) elementarnych struktur. 4. Struktura gl(h) pojawiająca się na obu semiwariogramach jednostkowych ii(h) i jj(h) nie musi być obecna na kros semiwariogramie ij(h) obu zmiennych.

Najlepiej dopasowane modele izotropowe dla cech b 1_03 b i b 3 n_03 b tworzone jednocześnie zgodnie z zasadami LCM niezależnie b 1_03 b gamma(h) = 18, 0 + 78, 0 Sph(95) + 82, 0 Sph(628) b 3 n_03 b gamma(h) = 50, 0 + 49, 0 Sph(84) + 96, 5 Sph(589) b 1 -b 3 n_03 b gamma(h) = 22, 0 + 52, 8 Sph(150) + 72, 0 Sph(587) b 1_03 b gamma(h) = 19, 63563 + 78, 41449 Sph(95) + 76, 70560 Sph(620) b 3 n_03 b gamma(h) = 54, 82879 + 48, 98145 Sph(95) + 91, 90548 Sph(620) b 1 -b 3 n_03 b gamma(h) = 16, 46937 + 53. 95995 Sph(95) + 77, 51083 Sph(620)

Testowanie kryterium połowicznej pozytywnej określoności macierzy współczynników b 1_03 b gamma(h) = 19, 63563 + 78, 41449 Sph(95) + 76, 70560 Sph(620) b 3 n_03 b gamma(h) = 54, 82879 + 48, 98145 Sph(95) + 91, 90548 Sph(620) b 1 -b 3 n_03 b gamma(h) = 16, 46937 + 53. 95995 Sph(95) + 77, 51083 Sph(620) Macierz współczynników struktury nuggetowej Macierz współczynników 1 struktury sferycznej Macierz współczynników 2 struktury sferycznej

Testowanie kryterium połowicznej pozytywnej określoności macierzy współczynników • 3 pierwsze nierówności są spełnione ponieważ wszystkie elementy przekątne każdej macierzy nie są negatywne.

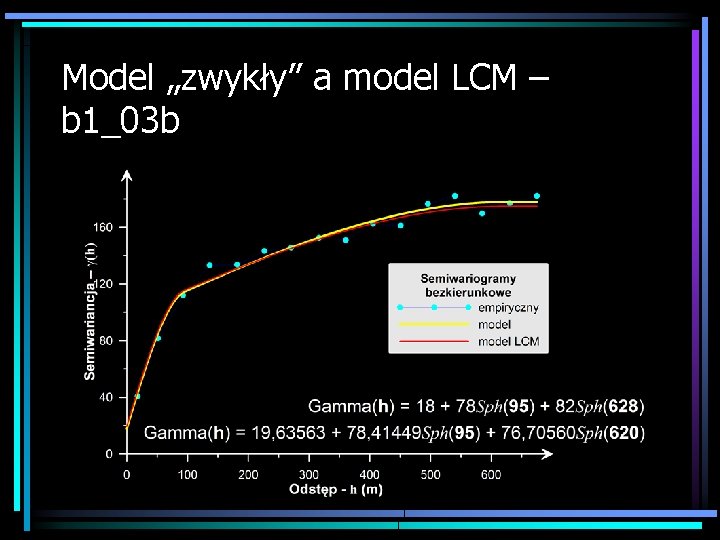
Model „zwykły” a model LCM – b 1_03 b

Model „zwykły” a model LCM – b 3 n_03 b

Uproszczony model koregionalizacji • LCM jest bardzo skomplikowany; wymaga poszukiwania optymalnego rozwiązania metodą prób i błędów, albo posiadania oprogramowania wykonującego to zadanie metodą iteracyjną opracowaną na początku lat 90 -tych XX wieku (Goulard, Voltz 1992, program LCMFIT 2) • W ostatnim 15 -leciu opracowano dwa uproszczone modele koregionalizacji szczególnie przydatne do kokrigingu kolokacyjnego (Almeida, Journel 1994, Journel 1998)

Uproszczony model koregionalizacji: model Markova I (MM 1) • W modelu Markowa I przyjmuje się następujące założenie dotyczące kroskorelogramu dwóch zmiennych Z i Y: gdzie z(h) = Cz(h)/Cz(0) jest korelogramem zmiennej pierwotnej, a zy(0) jest współczynnikiem korelacji pomiędzy zmienną pierwotną a wtórną określonym z par danych obu zmiennych znajdujących się w tej samej lokalizacji {z(ua), y(ua)}

Uproszczony model koregionalizacji: model Markova I (MM 1) • Do wykonania estymacji metodą kokrigingu przy użyciu modelu 1 Markova potrzebne są zatem jedynie: – model semiwariancji zmiennej pierwotnej, – współczynnik korelacji liniowej zmiennej pierwotnej z wtórną, – wariancja zmiennej wtórnej. • Model struktury przestrzennej zmiennej wtórnej jest obliczany na podstawie podanych wcześniej wzorów

Uproszczony model koregionalizacji: model Markova II (MM 2) • W modelu Markowa II przyjmuje się następujące założenie dotyczące kroskorelogramu dwóch zmiennych: gdzie y(h) = Cy(h)/Cy(0) jest korelogramem zmiennej wtórnej, a zy(0) jest współczynnikiem korelacji pomiędzy zmienną pierwotną a wtórną określonym z par danych obu zmiennych znajdujących się w tej samej lokalizacji {z 1(ua), y 2(ua)}

Uproszczony model koregionalizacji: model Markova I (MM 1) • Do wykonania estymacji metodą kokrigingu przy użyciu modelu 1 Markova potrzebne są zatem jedynie: – model semiwariancji zmiennej wtórnej, – model semiwariancji zmiennej pierwotnej, – współczynnik korelacji liniowej zmiennej pierwotnej z wtórną, • Ponieważ modele struktury przestrzennej zmiennej pierwotnej i wtórnej muszą być spójne z ich kroskorelogramem modelowanie dla zmiennej pierwotnej powinno być wykonywane przy pomocy liniowej kombinacji modelu zmiennej wtórnej i jakiegokolwiek innego dopuszczalnego modelu R(h):

Uproszczony model koregionalizacji: model Markova I (MM 1) Zasady tworzenia modelu struktury przestrzennej zmiennej pierwotnej: gdzie R(h) jest potrzebne do wprowadzenia do modelowania Cz(h) odpowiedniej liczby stopni swobody. Przy użyciu semiwariogramów zapisuje się to poniższy sposób: gdzie Cz(0) i Cy(0) to wariancje zmiennych pierwotnej i wtórnej, a R(h) to dowolny dozwolony model semiwariogramu z jednostkową wariancją progową.