Funes reais de varivel real Generalidades acerca de

Funções reais de variável real Generalidades acerca de funções reais de variável real O essencial

Função real de variável real Uma função f: A→B designa-se por função real de variável real se A e B estiverem contidos em IR. Quando uma função f está definida através de uma expressão, f(x), chamamos-lhe expressão analítica de f, e, quando nada for dito em contrário, esta expressão representa a função f com conjunto de chegada IR e domínio constituído por todos os números reais a para os quais a expressão f(a) tem significado em IR; ou seja, f(a) é um número real. Este processo de caracterizar f designa-se por definição (analítica) de f pela expressão f(a).

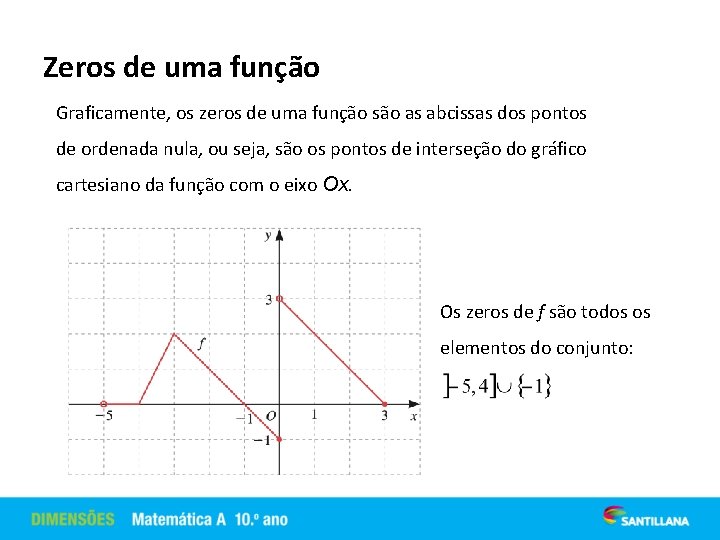
Zeros de uma função Dada uma função f, real de variável real, designa-se por zeros de f todos os valores x Df, tais que f (x) = 0. Exemplo: Seja f a função real de variável real, definida em IR por: . Os zeros de f são 2 e 3:

Zeros de uma função Graficamente, os zeros de uma função são as abcissas dos pontos de ordenada nula, ou seja, são os pontos de interseção do gráfico cartesiano da função com o eixo Ox. Os zeros de f são todos os elementos do conjunto:

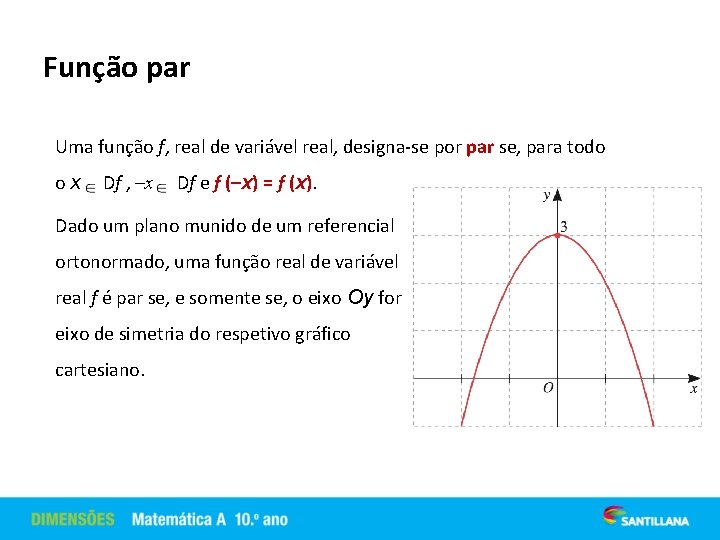
Função par Uma função f, real de variável real, designa-se por par se, para todo ox Df , –x Df e f (–x) = f (x). Dado um plano munido de um referencial ortonormado, uma função real de variável real f é par se, e somente se, o eixo Oy for eixo de simetria do respetivo gráfico cartesiano.

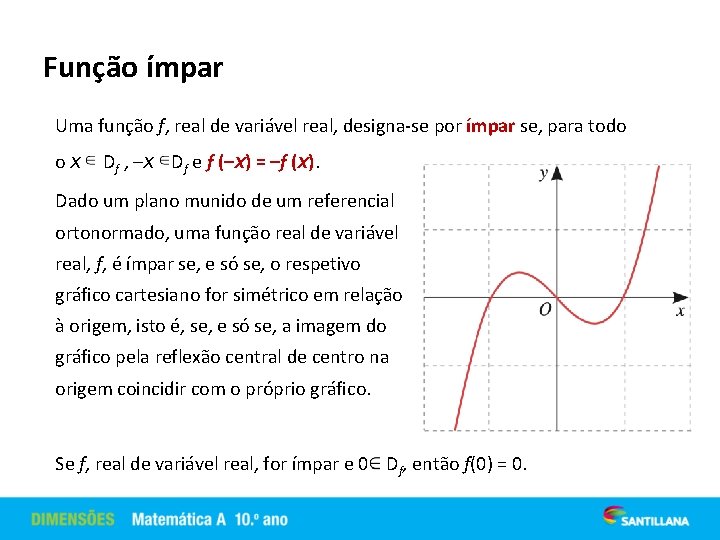
Função ímpar Uma função f, real de variável real, designa-se por ímpar se, para todo ox Df , –x Df e f (–x) = –f (x). Dado um plano munido de um referencial ortonormado, uma função real de variável real, f, é ímpar se, e só se, o respetivo gráfico cartesiano for simétrico em relação à origem, isto é, se, e só se, a imagem do gráfico pela reflexão central de centro na origem coincidir com o próprio gráfico. Se f, real de variável real, for ímpar e 0 Df, então f(0) = 0.

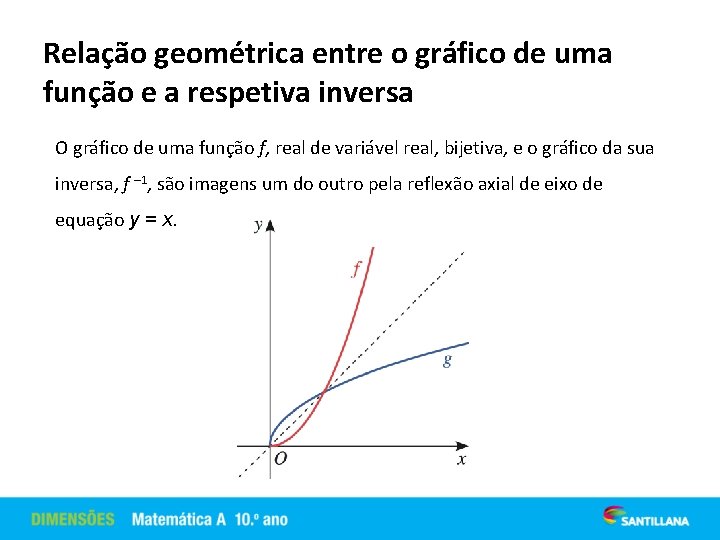
Relação geométrica entre o gráfico de uma função e a respetiva inversa O gráfico de uma função f, real de variável real, bijetiva, e o gráfico da sua inversa, f – 1, são imagens um do outro pela reflexão axial de eixo de equação y = x.

Translações verticais Dados uma função real de variável real f, um número real b não nulo e um plano munido de um referencial cartesiano, o gráfico cartesiano da função real de variável real definida em Dg = Df por g(x) = f(x) + b é a imagem do gráfico cartesiano de f pela translação de vetor .

Translações horizontais Dados uma função real de variável real f, um número real c não nulo e um plano munido de um referencial cartesiano, o gráfico cartesiano da função real de variável real definida em Dg ={x + c: x Df } por g(x) = f(x – c) é a imagem do gráfico cartesiano de f pela translação de vetor .

Translações Dados uma função real de variável real f, dois números reais c e d não nulos e um plano munido de um referencial cartesiano, o gráfico cartesiano da função real de variável real definida em Dg ={x + c: x Df } por g(x) = f(x – c) + d é a imagem do gráfico cartesiano de f pela translação de vetor .

Contrações/Dilatações verticais Dados um plano munido de um referencial cartesiano e um número real 0 < a < 1 (respetivamente, a > 1), designa-se por contração vertical (respetivamente, dilatação vertical) de coeficiente a a transformação Φ do plano, que a cada ponto P(x, y) associa o ponto Φ(P) de coordenadas (x, ay). Ou seja, dada uma função f, o gráfico cartesiano da função g de domínio Dg = Df, definida por g(x) = af(x), é imagem do gráfico cartesiano de f pela contração vertical (respetivamente, pela dilatação vertical) de coeficiente a.

Contrações/Dilatações horizontais Dados um plano munido de um referencial cartesiano e um número real 0 < a < 1 (respetivamente, a > 1), designa-se por contração horizontal (respetivamente, dilatação horizontal) de coeficiente a a transformação Φ do plano, que a cada ponto P(x, y) associa o ponto Φ(P) de coordenadas (ax, y). Ou seja, dada uma função f, o gráfico cartesiano da função g de domínio , definida por g(x) = f(ax), é imagem do gráfico cartesiano de f pela dilatação horizontal (respetivamente, pela contração horizontal) de coeficiente .

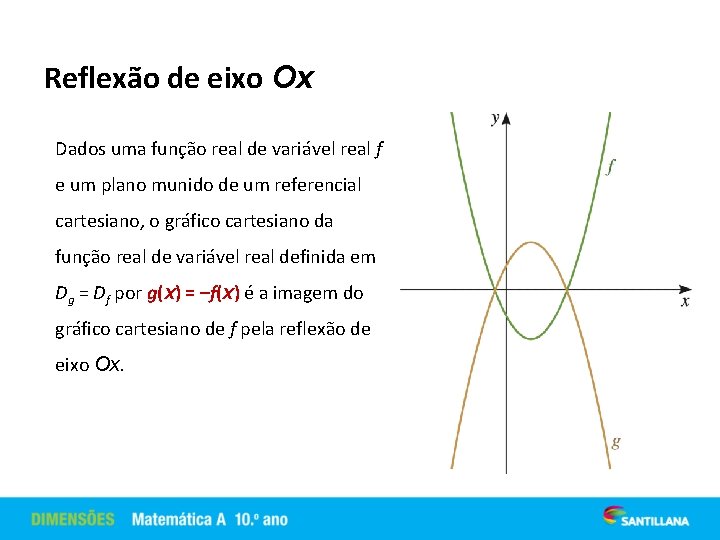
Reflexão de eixo Ox Dados uma função real de variável real f e um plano munido de um referencial cartesiano, o gráfico cartesiano da função real de variável real definida em Dg = Df por g(x) = –f(x) é a imagem do gráfico cartesiano de f pela reflexão de eixo Ox.

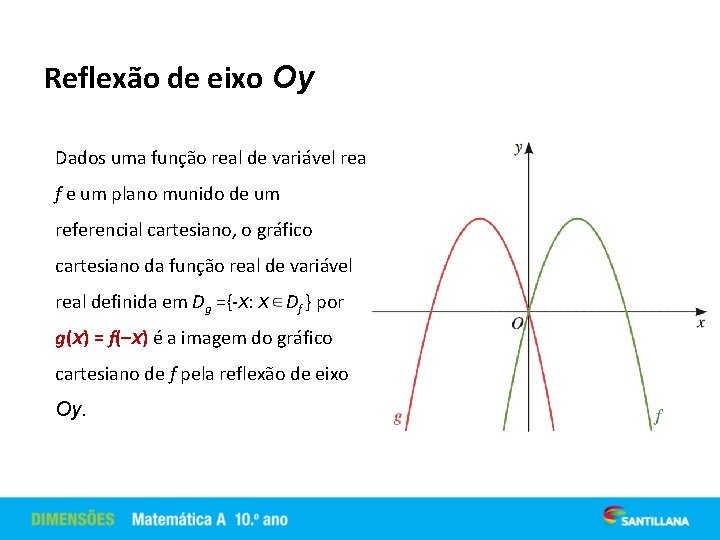
Reflexão de eixo Oy Dados uma função real de variável real f e um plano munido de um referencial cartesiano, o gráfico cartesiano da função real de variável real definida em Dg ={-x: x Df } por g(x) = f(–x) é a imagem do gráfico cartesiano de f pela reflexão de eixo Oy.