Funes reais de varivel real Generalidades acerca de

Funções reais de variável real Generalidades acerca de funções O essencial

Conceito de função Dados dois conjuntos A e B, fica definida uma função f (ou aplicação) de A em B quando a qualquer elemento x de A se associa um, e um só, elemento de B, representado por f(x). • Um elemento x de A designa-se por objeto e o seu correspondente em B, f(x), por imagem de x. • O conjunto A designa-se por domínio de f e representa-se por Df. • O conjunto B designa-se por conjunto de chegada. • O conjunto das imagens designa-se por contradomínio de f e representa-se por D’f, CDf ou f(A). • Escreve-se f: A→B para notar que f é uma função de A em B.

Produto cartesiano de conjuntos Dados dois conjuntos A e B, designa-se por produto cartesiano de A por B o conjunto dos pares ordenados (a, b), tais que a e b pertencem a A e B, respetivamente, ou seja, Este conjunto representa-se por A × B. .

Gráfico de uma função Dada uma função f: A→B, o conjunto , subconjunto de A × B, designa-se por gráfico de f.

Igualdade de funções Duas funções f e g são iguais ( f = g ) se, e somente se: • têm o mesmo domínio; • têm o mesmo conjunto de chegada; • cada elemento do domínio tem a mesma imagem por f e por g.

Restrição de uma função Dados dois conjuntos A e B, uma função f: A→B e um conjunto C, a função definida de C ∩ A em B, que a cada valor de x faz corresponder f(x) (imagem de x por f), designa-se por restrição de f a C e representa-se por f|C, isto é, a restrição de f a C é a função f|C: C ∩ A →B , tal que: .

Conjunto imagem Dados dois conjuntos A e B, uma função f: A→B e um conjunto C A, designa-se por conjunto imagem de C por f e representa-se por f(C) o conjunto das imagens por f dos elementos de C. Este conjunto pode também ser representado por:

Função injetiva Dados dois conjuntos A e B, uma função f: A→B designa-se por função injetiva se, e somente se: De forma equivalente, uma função f: A→B é injetiva se:

Função sobrejetiva Dados dois conjuntos A e B, uma função f: A→B designa-se por função sobrejetiva se para todo y B existe pelo menos um x A, tal que y = f(x), isto é, o equivalentemente a f(A) = B. Uma função sobrejetiva de A em B designa-se por sobrejeção de A em B ou função de A sobre B.

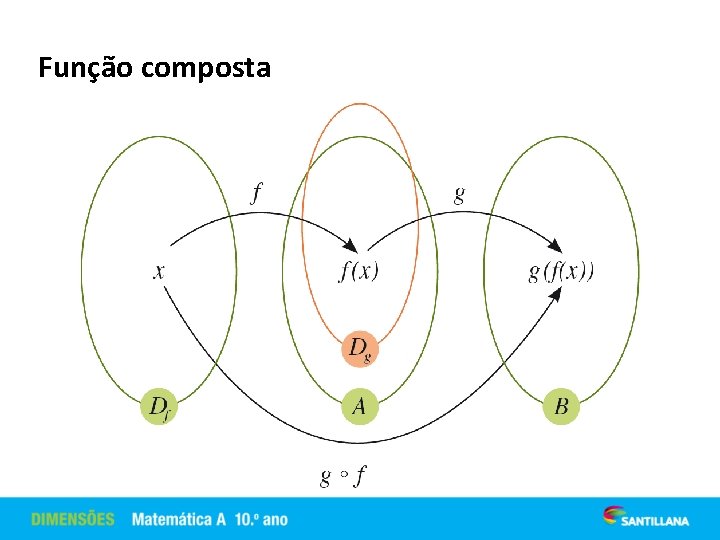
Função composta Dadas duas funções f: Df →A e g: Dg→B, designa-se por função composta de g com f e representa-se por g o f a função g o f : Dg o f →B, tal que: e A função g o seguida de g. f designa-se também por g composta com f, g após f ou f

Função composta

Função identidade Dado um conjunto A, designa-se por função identidade em A e representa -se por Id. A a função Id. A: A→A, tal que: . Dado um conjunto A, a função identidade em A é bijetiva.

Função inversa Dados dois conjuntos A e B, uma função f: A→B bijetiva, designa-se por função inversa de f e representa-se por f – 1 a função f -1: B → A, tal que: . Dada uma função f: A→B bijetiva: • a sua inversa, f – 1: B → A, também é bijetiva; • a inversa de f – 1 é f, ou seja, (f – 1) – 1=f. A função f – 1 também se designa por bijeção recíproca de f.

Função composta e função inversa Dados dois conjuntos A e B, uma função f: A→B é uma função bijetiva se, e somente se, existe uma função g: B→A, tal que: e . Tal função g é a função inversa de f, ou seja, g = f – 1.