Funcin Cuadrtica Se llama funcin cuadrtica a la

Función Cuadrática Se llama función cuadrática a la función que tiene asociada en su fórmula un polinomio de grado 2 f(x) = a x 2 + bx + c, donde a, b y c son números reales y a ≠ 0 Se llama ecuación cuadrática a toda ecuación que pueda expresarse de la forma a x 2 + b x + c=0 con a ≠ 0 Donde: ax 2 se llama término cuadrático y el valor real no nulo: a se llama coeficiente cuadrático bx se llama término lineal c y el valor real: b se llama coeficiente lineal Ejemplo: Toda ecuación cuadrática puede expresarse de tres formas: siendo siempre a ≠ 0 FORMA CANÓNICA: a (x – xv)2 + yv = 0 FORMA POLINÓMICA: ax 2 + bx + c = 0 FORMA FACTOREADA: a (x – x 1) (x – x 2) = 0 (si las raíces son reales) se llama término independiente.

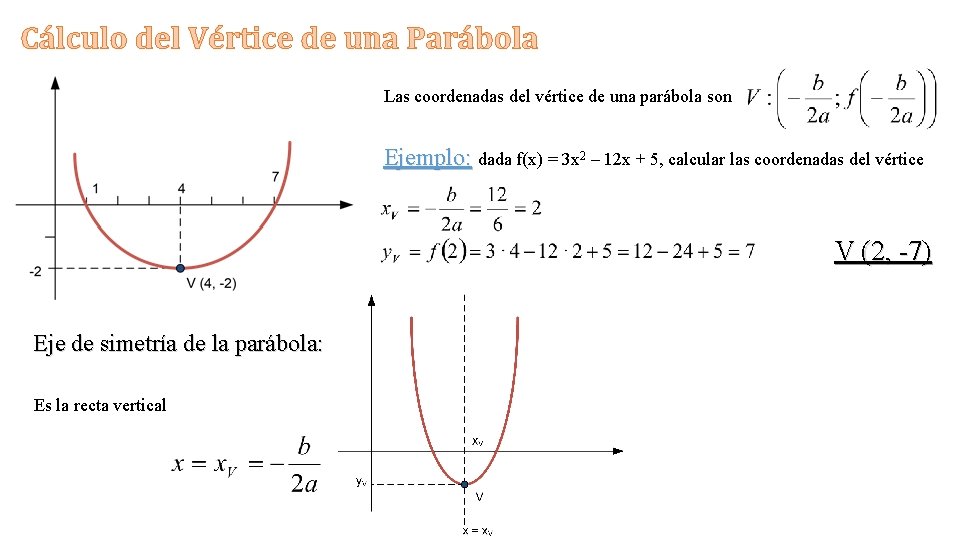
Cálculo del Vértice de una Parábola Las coordenadas del vértice de una parábola son Ejemplo: dada f(x) = 3 x 2 – 12 x + 5, calcular las coordenadas del vértice V (2, -7) Eje de simetría de la parábola: Es la recta vertical

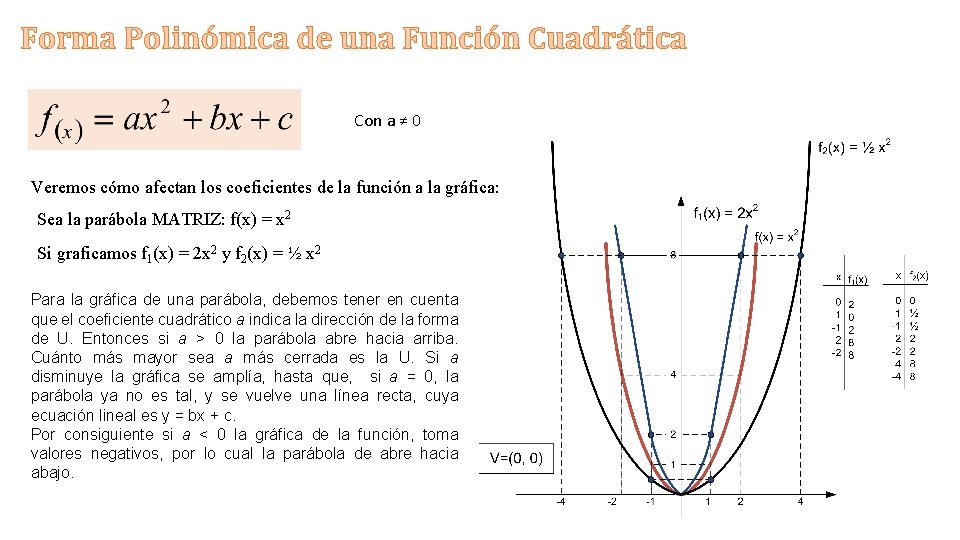
Forma Polinómica de una Función Cuadrática Con a ≠ 0 Veremos cómo afectan los coeficientes de la función a la gráfica: Sea la parábola MATRIZ: f(x) = x 2 Si graficamos f 1(x) = 2 x 2 y f 2(x) = ½ x 2 Para la gráfica de una parábola, debemos tener en cuenta que el coeficiente cuadrático a indica la dirección de la forma de U. Entonces si a > 0 la parábola abre hacia arriba. Cuánto más mayor sea a más cerrada es la U. Si a disminuye la gráfica se amplía, hasta que, si a = 0, la parábola ya no es tal, y se vuelve una línea recta, cuya ecuación lineal es y = bx + c. Por consiguiente si a < 0 la gráfica de la función, toma valores negativos, por lo cual la parábola de abre hacia abajo.

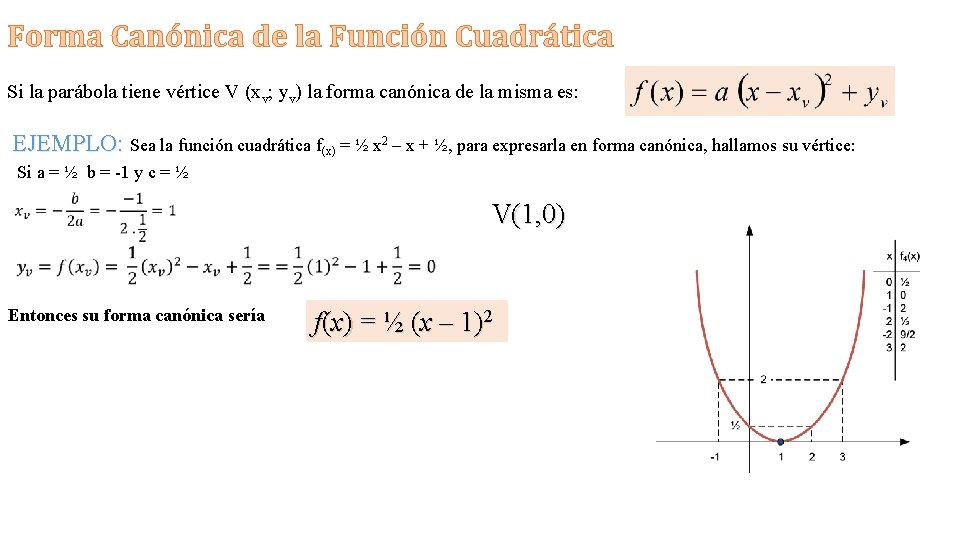
Forma Canónica de la Función Cuadrática Si la parábola tiene vértice V (xv; yv) la forma canónica de la misma es: EJEMPLO: Sea la función cuadrática f(x) = ½ x 2 – x + ½, para expresarla en forma canónica, hallamos su vértice: Si a = ½ b = -1 y c = ½ V(1, 0) Entonces su forma canónica sería f(x) = ½ (x – 1)2

Ceros o Raíces de la Función Cuadrática Las raíces de la función, son los valores de x para los cuales f(x) = 0. Para hallarlos debemos saber cuáles son los x para los cuáles ax 2 + bx + c = 0 y eso lo hacemos con la fórmula resolvente. Geométricamente, como en cualquier función numérica los x para los cuales f(x) = 0, son los puntos, si existen, donde la gráfica corta o interseca al eje “x”. Ejemplo: Si tenemos f(x) = x 2 – 5 x + 6 a = 1, b = -5 y c = 6 lo aplico a la fórmula resolvente Las raíces o ceros de la función son: x 1 = 3 x 2 = 2

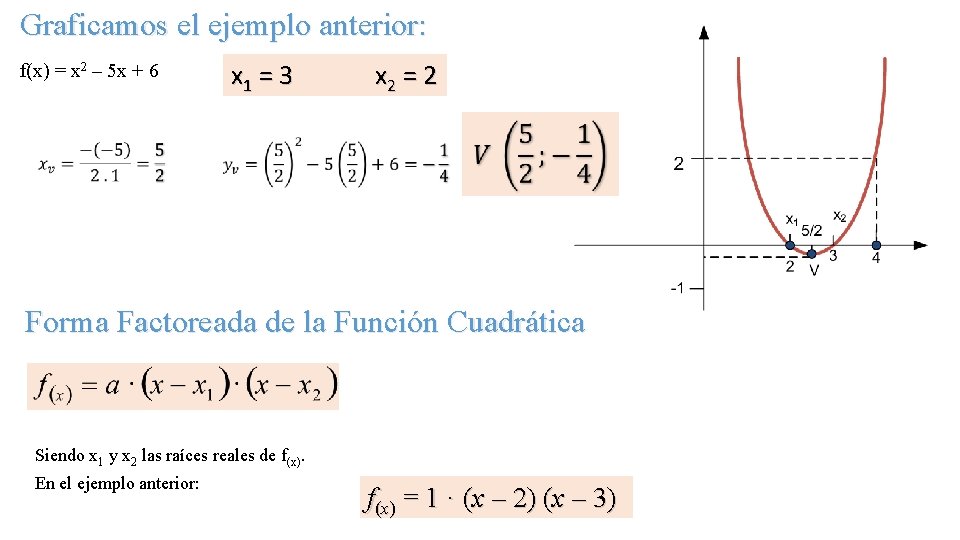
Graficamos el ejemplo anterior: f(x) = x 2 – 5 x + 6 x 1 = 3 x 2 = 2 Forma Factoreada de la Función Cuadrática Siendo x 1 y x 2 las raíces reales de f(x). En el ejemplo anterior: f(x) = 1 · (x – 2) (x – 3)