Sesin Contenidos Funcin cuadrtica 10 Elementos de la

Sesión Contenidos: ↘ Función cuadrática. 10 > Elementos de la función cuadrática. ↘ Gráfico de funciones cuadráticas en el plano cartesiano. Profesor: Víctor Manuel Reyes F. Asignatura: Matemática para Ciencias de la Salud (MAT-011) Primer Semestre 2012

Aprendizajes esperados: > Determinar la concavidad de la parábola y los ceros de la función a partir de la función cuadrática dada algebraicamente. > Determinar el vértice de la parábola. > Grafica funciones cuadráticas. > Determinar dominio, recorrido, intervalos de crecimiento y decrecimiento, a partir de la función dada algebraicamente y/o su gráfica. > Resolver ejercicios de aplicación (con enunciado verbal), que se comportan cuadráticamente.

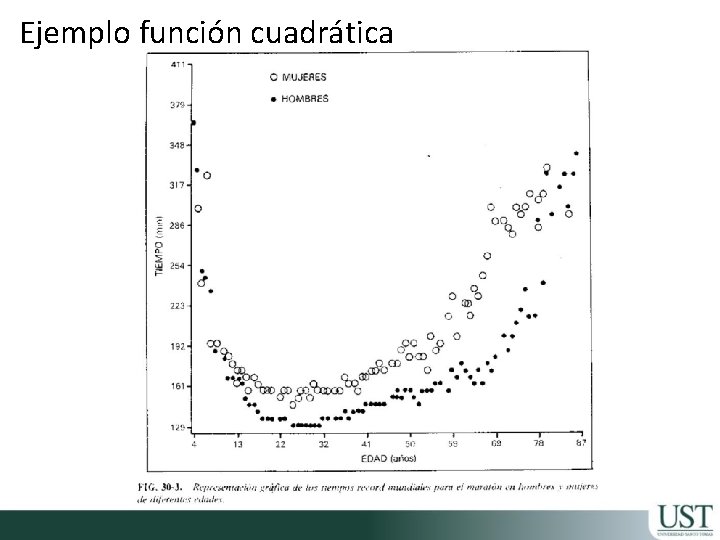
Ejemplo función cuadrática

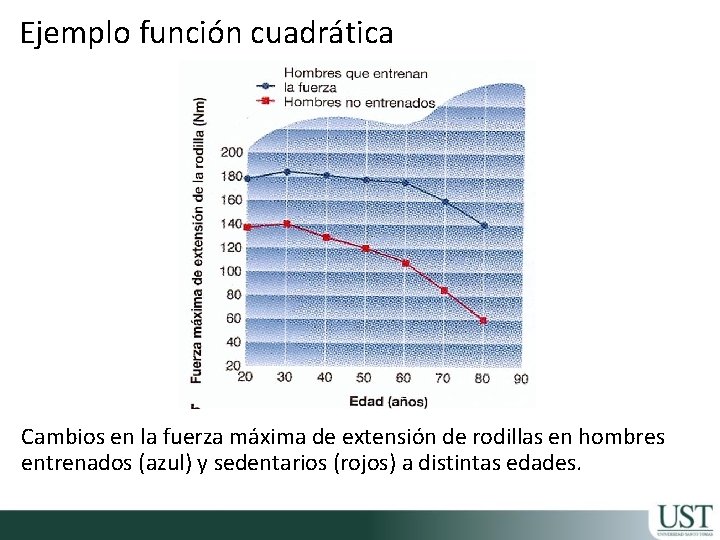
Ejemplo función cuadrática Cambios en la fuerza máxima de extensión de rodillas en hombres entrenados (azul) y sedentarios (rojos) a distintas edades.

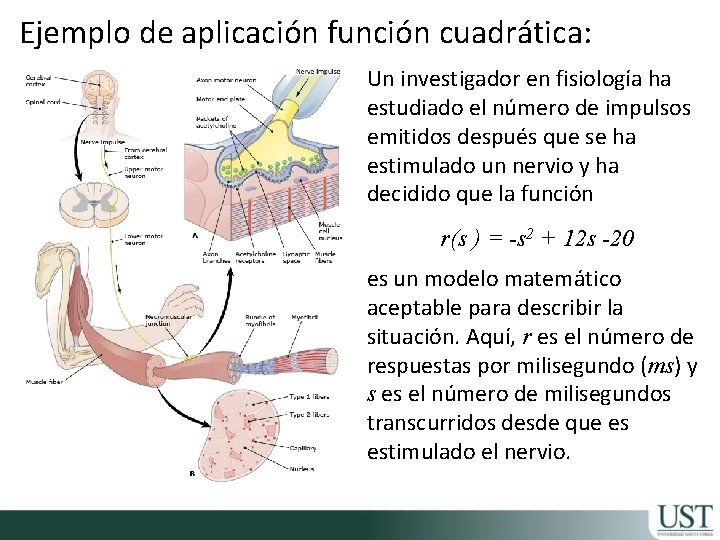
Ejemplo de aplicación función cuadrática: Un investigador en fisiología ha estudiado el número de impulsos emitidos después que se ha estimulado un nervio y ha decidido que la función r(s ) = -s 2 + 12 s -20 es un modelo matemático aceptable para describir la situación. Aquí, r es el número de respuestas por milisegundo (ms) y s es el número de milisegundos transcurridos desde que es estimulado el nervio.

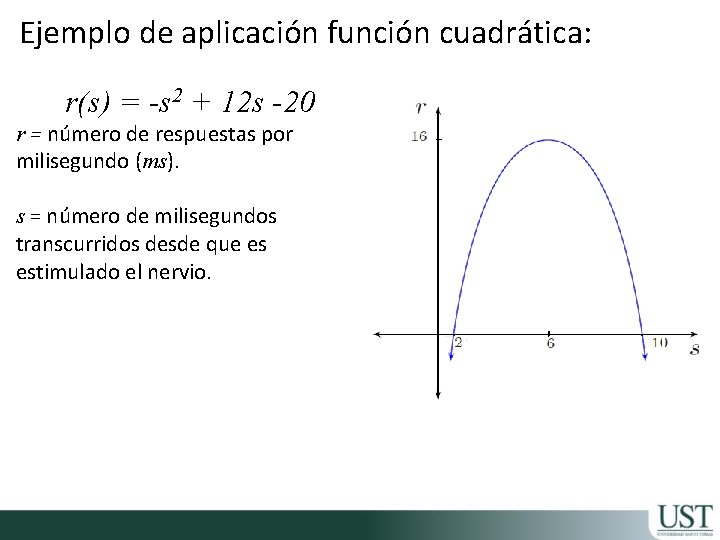
Ejemplo de aplicación función cuadrática: r(s) = -s 2 + 12 s -20 r = número de respuestas por milisegundo (ms). s = número de milisegundos transcurridos desde que es estimulado el nervio.

Definición función cuadrática: Una función cuadrática es una expresión descrita algebraicamente por: y = f (x) = ax 2 + bx + c donde a, b, c son números reales y a ≠ 0.

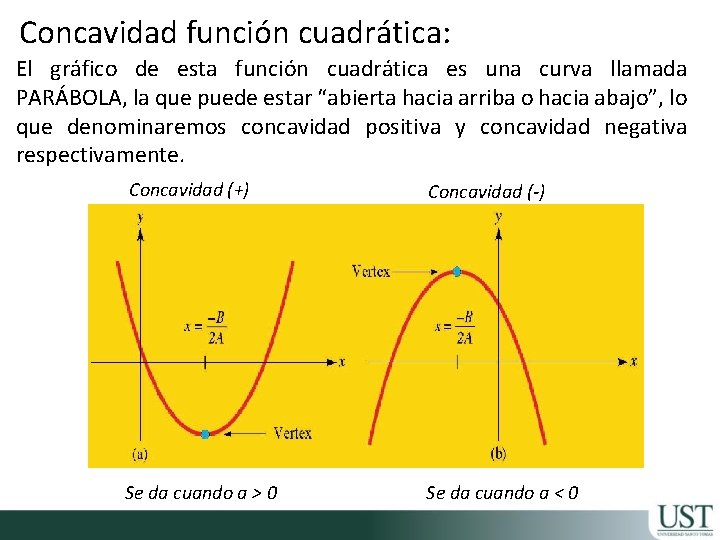
Concavidad función cuadrática: El gráfico de esta función cuadrática es una curva llamada PARÁBOLA, la que puede estar “abierta hacia arriba o hacia abajo”, lo que denominaremos concavidad positiva y concavidad negativa respectivamente. Concavidad (+) Concavidad (-) Se da cuando a > 0 Se da cuando a < 0

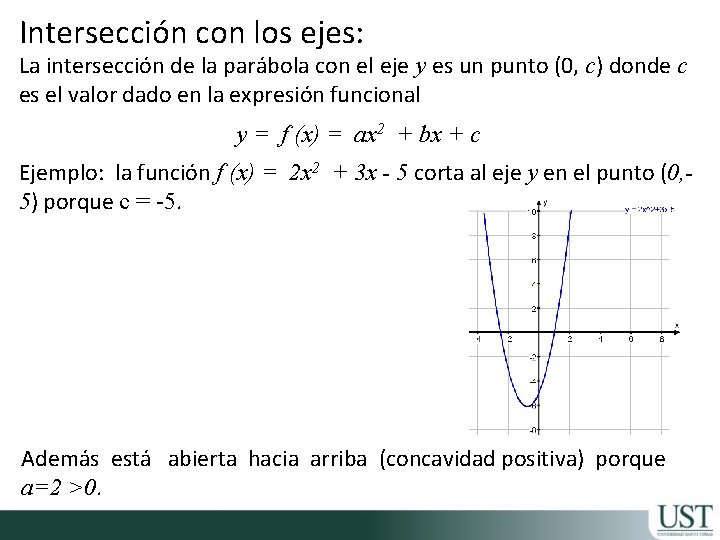
Intersección con los ejes: La intersección de la parábola con el eje y es un punto (0, c) donde c es el valor dado en la expresión funcional y = f (x) = ax 2 + bx + c Ejemplo: la función f (x) = 2 x 2 + 3 x - 5 corta al eje y en el punto (0, 5) porque c = -5. Además está abierta hacia arriba (concavidad positiva) porque a=2 >0.

Intersección con los ejes: La intersección con el eje x, se determina cuando la gráfica intercepte el eje x, debe ocurrir que y = 0; si reemplazamos en la ecuación, obtenemos: 0= ax 2 + bx + c, por lo tanto las intersecciones de la función cuadrática con el eje x se obtienen resolviendo las ecuación de segundo grado. » Por factorización » Utilizando la fórmula » Por completación de cuadrados

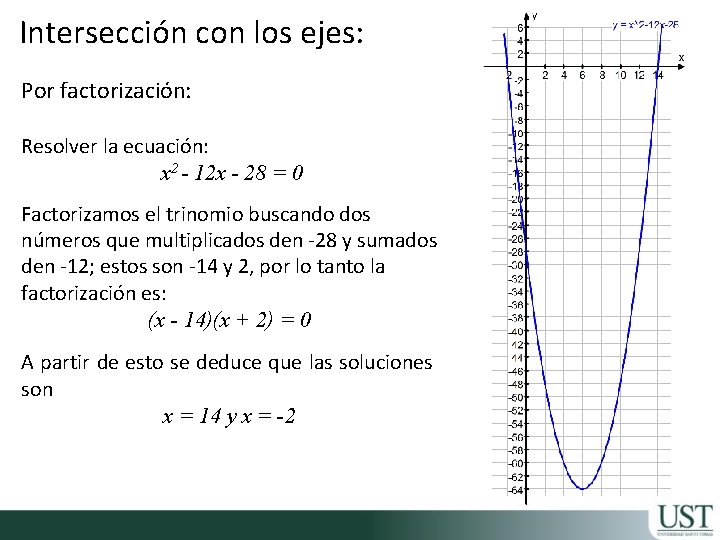
Intersección con los ejes: Por factorización: Resolver la ecuación: x 2 - 12 x - 28 = 0 Factorizamos el trinomio buscando dos números que multiplicados den -28 y sumados den -12; estos son -14 y 2, por lo tanto la factorización es: (x - 14)(x + 2) = 0 A partir de esto se deduce que las soluciones son x = 14 y x = -2

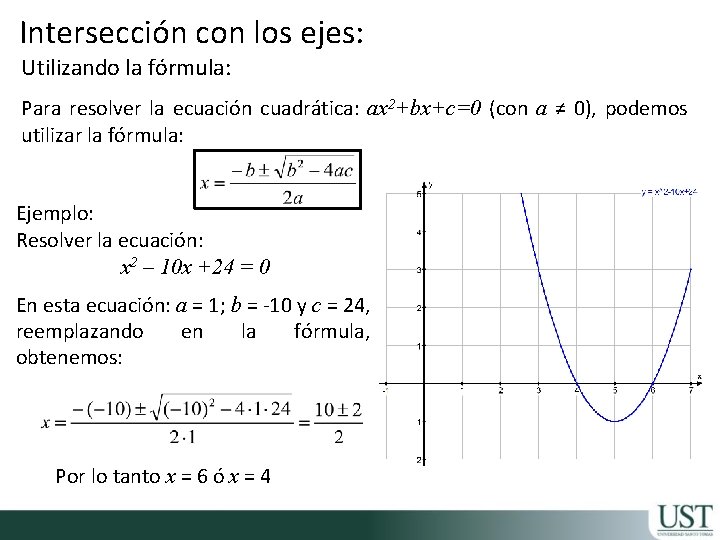
Intersección con los ejes: Utilizando la fórmula: Para resolver la ecuación cuadrática: ax 2+bx+c=0 (con a ≠ 0), podemos utilizar la fórmula: Ejemplo: Resolver la ecuación: x 2 – 10 x +24 = 0 En esta ecuación: a = 1; b = -10 y c = 24, reemplazando en la fórmula, obtenemos: Por lo tanto x = 6 ó x = 4

Intersección con los ejes: Las soluciones de una ecuación ax 2+bx+c=0 dependen del signo del discriminante que es la cantidad subradical de la fórmula Lo que se denota Así tenemos que: 1. Si Δ > 0, la ecuación tiene soluciones reales y distintas, por lo tanto la parábola corta en dos puntos al eje x. 2. Si Δ = 0, la ecuación tiene soluciones reales iguales, por lo tanto la parábola es tangente al eje x. 3. Si Δ < 0, la ecuación no tiene soluciones reales, por lo tanto la parábola no corta el eje x.

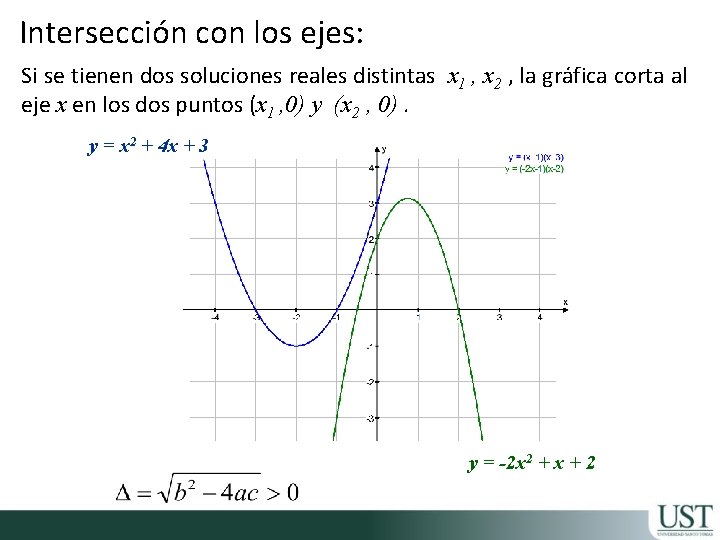
Intersección con los ejes: Si se tienen dos soluciones reales distintas x 1 , x 2 , la gráfica corta al eje x en los dos puntos (x 1 , 0) y (x 2 , 0). y = x 2 + 4 x + 3 y = -2 x 2 + x + 2

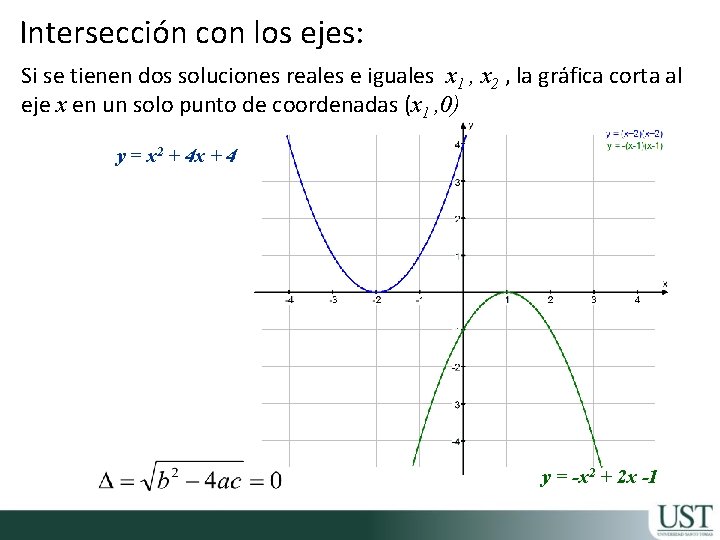
Intersección con los ejes: Si se tienen dos soluciones reales e iguales x 1 , x 2 , la gráfica corta al eje x en un solo punto de coordenadas (x 1 , 0) y = x 2 + 4 x + 4 y = -x 2 + 2 x -1

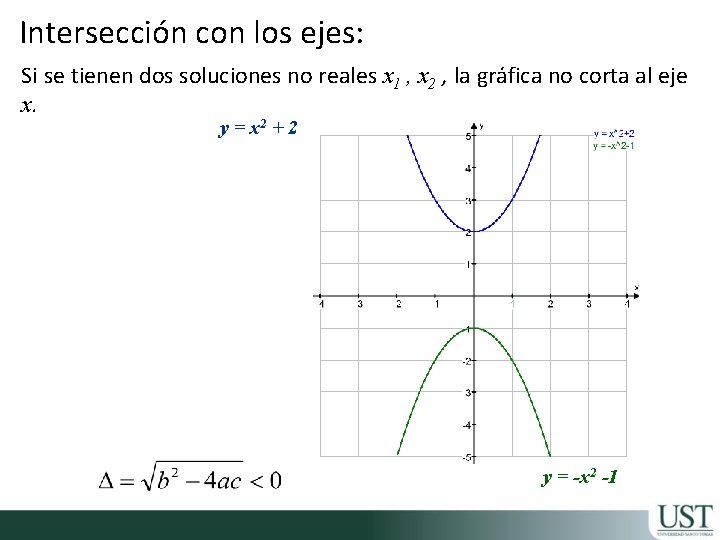
Intersección con los ejes: Si se tienen dos soluciones no reales x 1 , x 2 , la gráfica no corta al eje x. y = x 2 + 2 y = -x 2 -1

Coordenadas del vértice de la parábola: Otro de los elementos importantes para elaborar una buena gráfica de la parábola es conocer las coordenadas del vértice de una parábola, que es el punto donde “da la vuelta”. La fórmula del vértice, en función de los coeficientes a, b, c es: Si la parábola tiene concavidad positiva, decimos que V es un punto mínimo de la función. Si la parábola tiene concavidad negativa, V es punto máximo de la función.

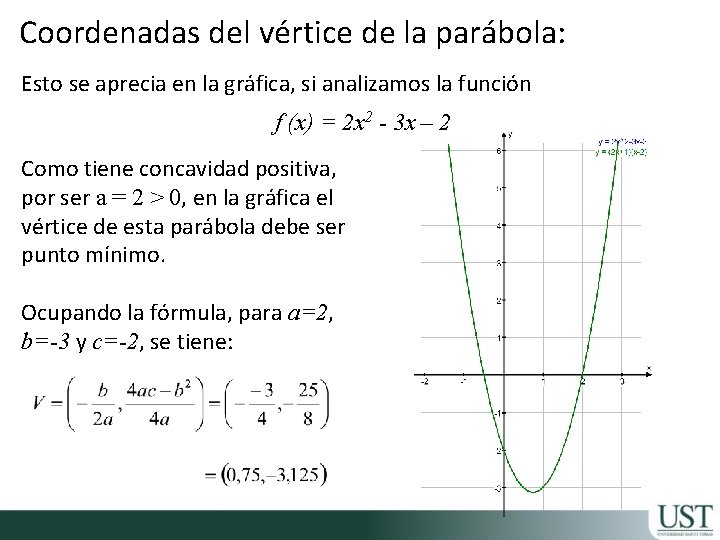
Coordenadas del vértice de la parábola: Esto se aprecia en la gráfica, si analizamos la función f (x) = 2 x 2 - 3 x – 2 Como tiene concavidad positiva, por ser a = 2 > 0, en la gráfica el vértice de esta parábola debe ser punto mínimo. Ocupando la fórmula, para a=2, b=-3 y c=-2, se tiene:

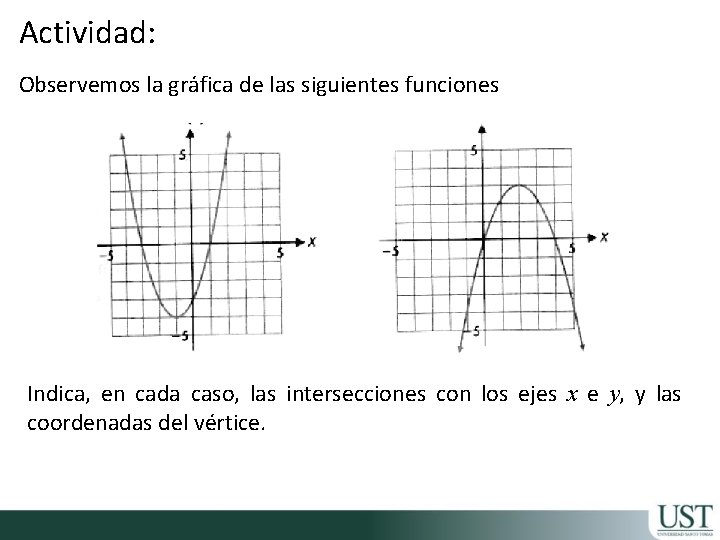
Actividad: Observemos la gráfica de las siguientes funciones Indica, en cada caso, las intersecciones con los ejes x e y, y las coordenadas del vértice.