Funcin cuadrtica y Ecuacin de segundo grado APRENDIZAJES

Función cuadrática y Ecuación de segundo grado

APRENDIZAJES ESPERADOS • Conocer y aplicar los conceptos matemáticos asociados al estudio de la función cuadrática. • Graficar una función cuadrática, determinando vértice, eje de simetría y concavidad. • Indicar las características gráficas de una parábola a través del análisis del discriminante. • Determinar las intersecciones de la parábola con los ejes cartesianos. • Determinar las raíces de una ecuación de 2º grado.

Contenidos 1. Función cuadrática 1. 1 Intersección con el eje Y 1. 2 Concavidad 1. 3 Eje de simetría y vértice 1. 4 Discriminante 2. Ecuación de 2º grado 2. 1 Raíces de una ecuación cuadrática 2. 2 Propiedades de las raíces 2. 3 Discriminante

1. Función Cuadrática Es de la forma: f(x) = ax 2 + bx + c con a =0; a, b, c IR y su gráfica es una parábola. Ejemplos: a) Si f(x) = 2 x 2 + 3 x + 1 a = 2, b = 3 b) Si f(x) = 4 x 2 - 5 x - 2 y c=1 a = 4, b = -5 y c = -2

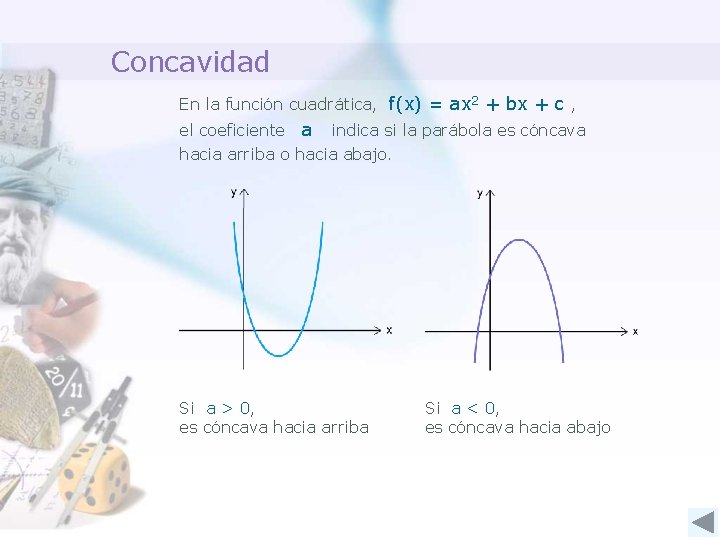
Concavidad En la función cuadrática, f(x) = ax 2 + bx + c , el coeficiente a indica si la parábola es cóncava hacia arriba o hacia abajo. Si a > 0, es cóncava hacia arriba Si a < 0, es cóncava hacia abajo

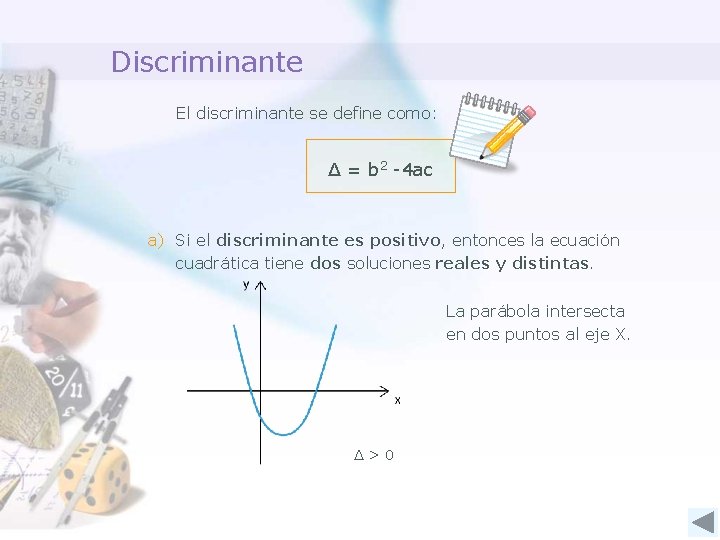
Discriminante El discriminante se define como: Δ = b 2 -4 ac a) Si el discriminante es positivo, entonces la ecuación cuadrática tiene dos soluciones reales y distintas. La parábola intersecta en dos puntos al eje X. Δ>0

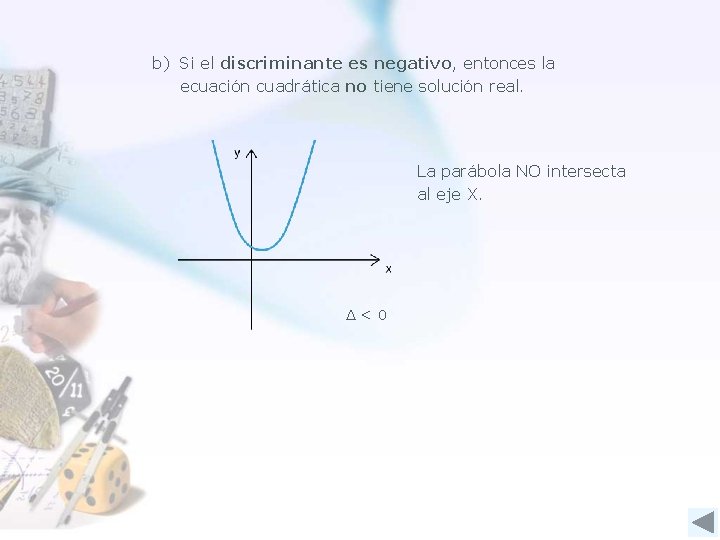
b) Si el discriminante es negativo, entonces la ecuación cuadrática no tiene solución real. La parábola NO intersecta al eje X. Δ<0

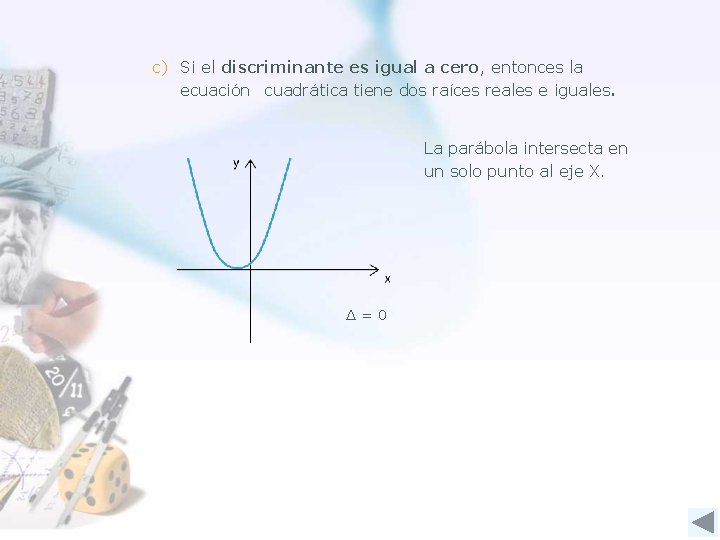
c) Si el discriminante es igual a cero, entonces la ecuación cuadrática tiene dos raíces reales e iguales. La parábola intersecta en un solo punto al eje X. Δ=0

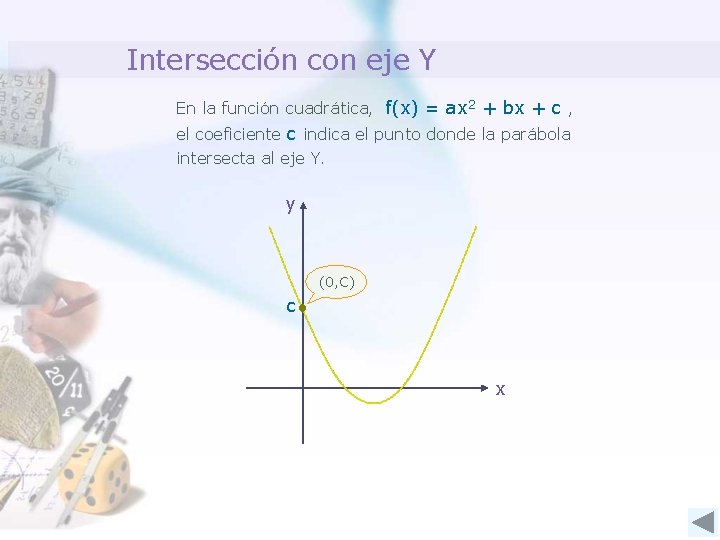
Intersección con eje Y En la función cuadrática, f(x) = ax 2 + bx + c , el coeficiente c indica el punto donde la parábola intersecta al eje Y. y (0, C) c x

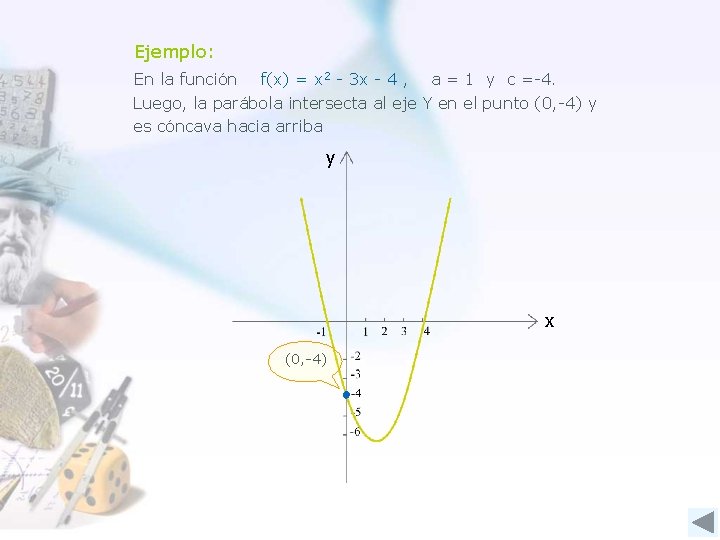
Ejemplo: En la función f(x) = x 2 - 3 x - 4 , a = 1 y c =-4. Luego, la parábola intersecta al eje Y en el punto (0, -4) y es cóncava hacia arriba y x (0, -4)

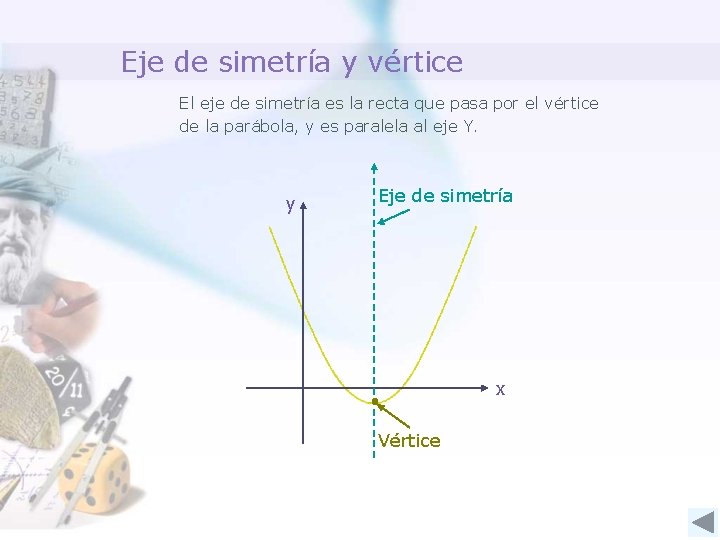
Eje de simetría y vértice El eje de simetría es la recta que pasa por el vértice de la parábola, y es paralela al eje Y. y Eje de simetría x Vértice

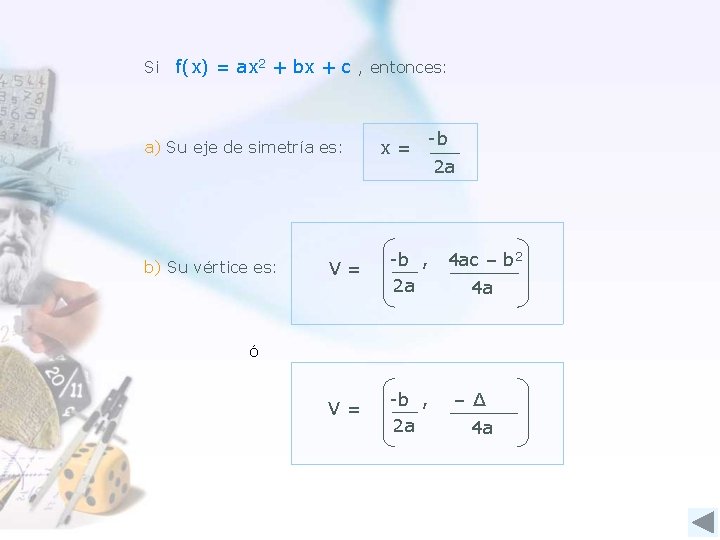
Si f(x) = ax 2 + bx + c , entonces: a) Su eje de simetría es: b) Su vértice es: x= -b V= -b , 2 a 2 a 4 ac – b 2 4 a ó – Δ 4 a

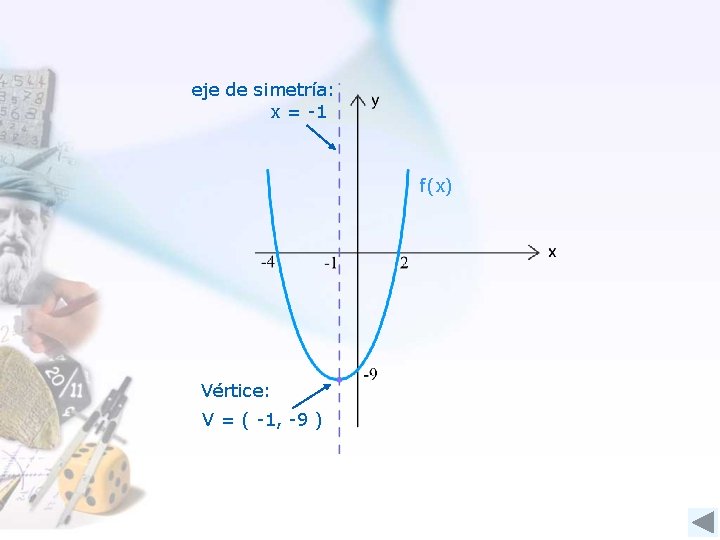
Ejemplo: En la función entonces: f(x) = x 2 + 2 x - 8, a = 1, b=2 y a) Su eje de simetría es: x= -b 2 a x= -2 2· 1 x = -1 b) Su vértice es: V= -b , 2 a 4 ac – b 2 4 a V = ( -1, -9 ) c = -8,

eje de simetría: x = -1 f(x) Vértice: V = ( -1, -9 )

Si la parábola es abierta hacia arriba, el vértice es un mínimo y si la parábola es abierta hacia abajo, el vértice es un máximo.

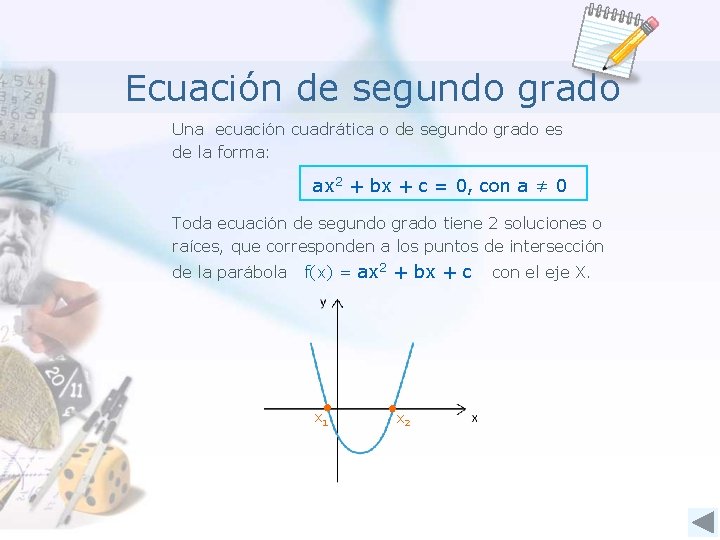
Ecuación de segundo grado Una ecuación cuadrática o de segundo grado es de la forma: ax 2 + bx + c = 0, con a ≠ 0 Toda ecuación de segundo grado tiene 2 soluciones o raíces, que corresponden a los puntos de intersección de la parábola f(x) = ax 2 + bx + c x 1 x 2 con el eje X.

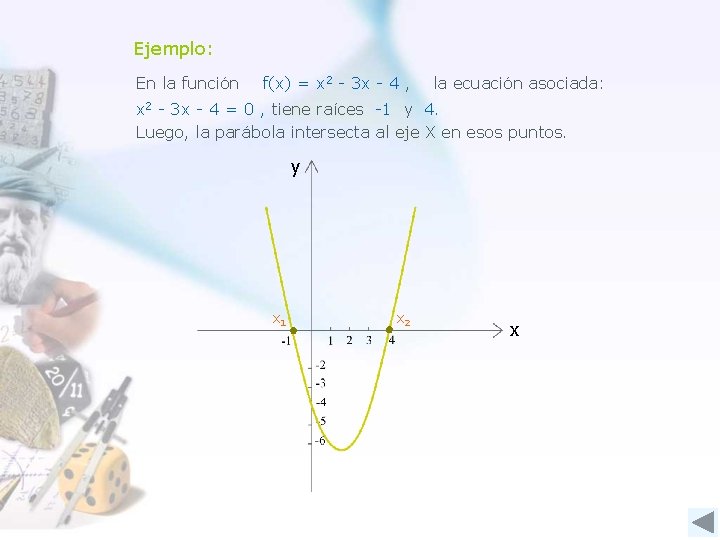
Ejemplo: En la función f(x) = x 2 - 3 x - 4 , la ecuación asociada: x 2 - 3 x - 4 = 0 , tiene raíces -1 y 4. Luego, la parábola intersecta al eje X en esos puntos. y x 1 x 2 x

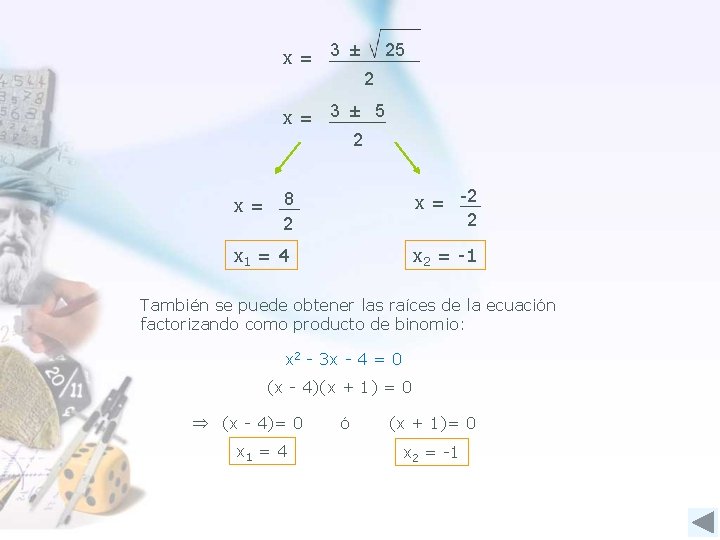
Raíces de una ecuación de 2° grado Fórmula para determinar las soluciones (raíces) de una ecuación de segundo grado: x= -b ± b 2 – 4 ac 2 a Ejemplo: Determinar las raíces de la ecuación: x 2 - 3 x - 4 = 0 x= -(-3) ± (-3)2 – 4· 1(- 4) 2 x= 3 ± 9 + 16 2

x= 3 ± 25 2 x= 3 ± 5 2 8 2 x = -2 2 x 1 = 4 x 2 = -1 x= También se puede obtener las raíces de la ecuación factorizando como producto de binomio: x 2 - 3 x - 4 = 0 (x - 4)(x + 1) = 0 (x - 4)= 0 x 1 = 4 ó (x + 1)= 0 x 2 = -1

Propiedades de las raíces Si x 1 y x 2 son las raíces de una ecuación de segundo grado de la forma ax 2 + bx + c = 0, entonces: 1) x 1 + x 2 = -b a 2) x 1 · x 2 = c a 3) x 1 - x 2 = ± Δ a Dadas las raíces o soluciones de una ecuación de segundo grado, se puede determinar la ecuación asociada a ellas. (x – x 1)(x – x 2) = 0

Pasos para graficar un Cuadrática. Paso Paso 1. 2. 3. 4. 5. 6. Calcular el Discriminante. Identificar la intersección con el eje Y. Calcular eje de Simetría. Calcular el Vértice. Solo si es que posee raíces, Calcularlas. Utilizando: Vértice + Intersección con el eje Y + raíces = Graficar