Fraktly Motivcia Pomocou 3 D modelovacch programov a

Fraktály

Motivácia · Pomocou 3 D modelovacích programov a techník, o ktorých sme si doteraz hovorili, vieme veľmi dobre modelovať veľké množstvo vecí – budovy, rôzne predmety, zvieratá, ľudí · Ťažko sa však modelujú rôzne zložité prírodné útvary – oblaky, dym, hory, pobrežia, niektoré rastliny a pod.

Motivácia

Fraktály · Fraktály sú útvary, ktorých základnou vlastnosťou je sebepodobnosť – znamená to, že obsahujú zmenšené kópie samých seba.

Fraktály

Fraktály v prírode

Fraktály v prírode

Fraktály v prírode

Sebepodobnosť · Sebepodobnosť (self-similarity) môže byť dvoch typov: · 1. Presná sebepodobnosť – hovoríme že množina A je presne sebepodobná, ak je zjednotením konečného počtu neprekrývajúcich sa transformovaných kópií samej seba: Transformácia i je škálovanie s koeficientom d (0, 1), ktoré môže byť zložené s otáčaním alebo posunutím. · Tento strom je zjednotením dvoch kópií samého seba: A= 1(A) 2(A) kde 1(A) je škálovanie zložené s otočením v smere hodinových ručičiek a s posunutím a 2(A) je rovnaké škálovanie zložené s otočením o rovnaký uhol proti smeru hodinových ručičiek a s rovnakým posunutím.

Sebepodobnosť · 2. Štatistická sebepodobnosť – hovoríme, že množina A je štatisticky sebepodobná, ak je zjednotením konečného počtu neprekrývajúcich sa transformovaných kópií samej seba, pričom každá z týchto kópií má rovnaké štatistické charakteristiky ako množina A (to býva väčšinou stredná hodnota alebo smerodajná odchýlka). Zápis je rovnaký ako v prvom prípade: Rozdiel je v tom, že transformácia i je zložená zo škálovania s koeficientom d (0, 1) a z ľubovoľnej inej transformácie, ktorá môže byť lineárna aj nelineárna. · Príkladom takejto sebepodobnosti sú hory alebo oblaky – v menšej mierke nenájdeme presné kópie celého objektu, ale objekty s veľmi podobnou štruktúrou ako celok.

Lineárne deterministické fraktály · Tieto fraktály sú presne sebepodobné a vznikajú jednoduchými rekurzívnymi postupmi, pri ktorých aplikujeme transformácie otáčania, posunutia a škálovania. · Uvedieme si niektoré najznámejšie príklady: 1. Cantorovo diskontinuum · Tento fraktál vzniká z úsečky tak, že z nej vyjmeme jej prostrednú tretinu. Potom tento postup opakujeme pre zostávajúce dve tretiny, ďalej pre štyri ďalšie vzniknuté časti atď. X Y Z · Z hľadiska transformácií dostaneme Cantorovo diskontinuum pomocou dvoch operácií. Najprv zoberieme celú množinu a preškálujeme ju s koeficientom 1/3 (z úsečky X dostaneme úsečku Y). Potom zoberieme celú množinu, preškálujeme ju s koeficientom 1/3 a potom posunieme o 2/3 pôvodnej dĺžky (z úsečky X dostaneme úsečku Z).

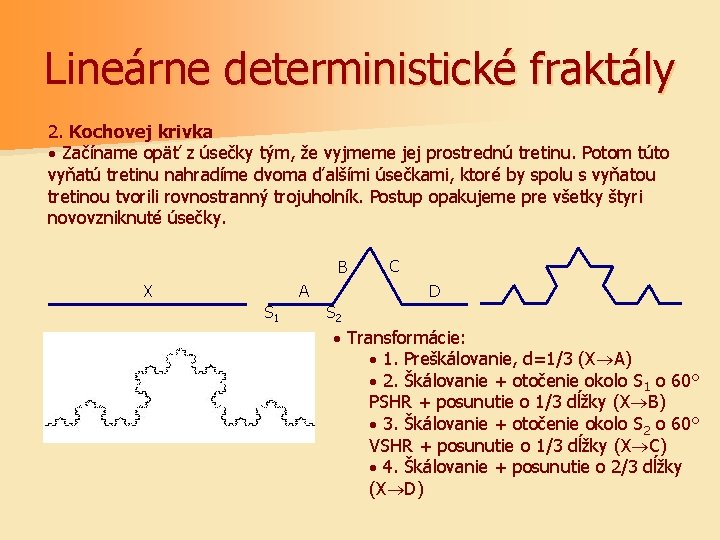
Lineárne deterministické fraktály 2. Kochovej krivka · Začíname opäť z úsečky tým, že vyjmeme jej prostrednú tretinu. Potom túto vyňatú tretinu nahradíme dvoma ďalšími úsečkami, ktoré by spolu s vyňatou tretinou tvorili rovnostranný trojuholník. Postup opakujeme pre všetky štyri novovzniknuté úsečky. B X A S 1 C D S 2 · Transformácie: · 1. Preškálovanie, d=1/3 (X A) · 2. Škálovanie + otočenie okolo S 1 o 60° PSHR + posunutie o 1/3 dĺžky (X B) · 3. Škálovanie + otočenie okolo S 2 o 60° VSHR + posunutie o 1/3 dĺžky (X C) · 4. Škálovanie + posunutie o 2/3 dĺžky (X D)

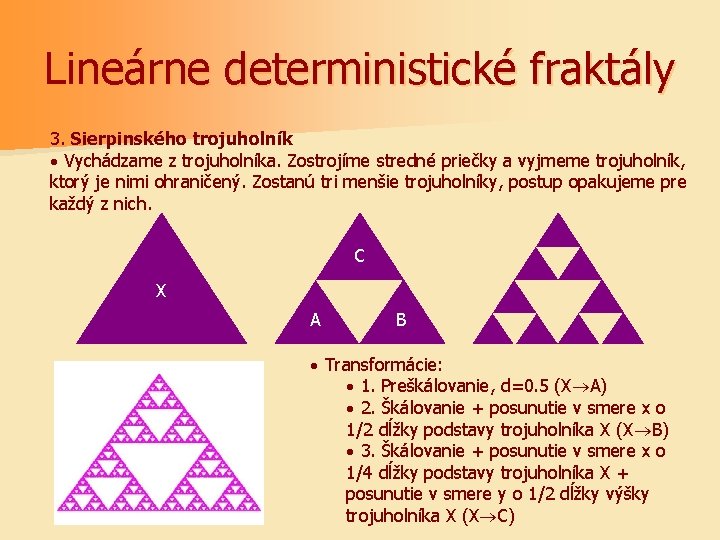
Lineárne deterministické fraktály 3. Sierpinského trojuholník · Vychádzame z trojuholníka. Zostrojíme stredné priečky a vyjmeme trojuholník, ktorý je nimi ohraničený. Zostanú tri menšie trojuholníky, postup opakujeme pre každý z nich. C X A B · Transformácie: · 1. Preškálovanie, d=0. 5 (X A) · 2. Škálovanie + posunutie v smere x o 1/2 dĺžky podstavy trojuholníka X (X B) · 3. Škálovanie + posunutie v smere x o 1/4 dĺžky podstavy trojuholníka X + posunutie v smere y o 1/2 dĺžky výšky trojuholníka X (X C)

Fraktálna dimenzia · Geometrické objekty obyčajne delíme na 1 D, 2 D, 3 D atď. Táto klasicky chápaná dimenzia sa nazýva topologická. · Pri charakteristike fraktálov si s topologickou dimenziou nevystačíme, keďže fraktály majú niektoré neobvyklé vlastnosti. · Predstavme si, že meriame úsečku. Najskôr použijeme hrubší meter, ktorý má dieliky dĺžky 1 m. Potom použijeme jemnejší meter s dielikmi dĺžky 1 cm. Dostaneme rovnaké výsledky. · Teraz si predstavme meranie nejakého členitejšieho objektu, napr. pobrežia. Pri meraní hrubším metrom, ktorý nie je schopný zachytiť malé nerovnosti, dostaneme menšiu dĺžku ako pri meraní jemnejším metrom (dĺžka portugalskošpanielskeho pobrežia bola pri metri v dielikom 100 km 987 km, pri metri s dielikom 1 km 1214 km). Toto je typická vlastnosť fraktálov.

Fraktálna dimenzia · Jedna z možných definícií fraktálnej dimenzie je takáto: · Majme útvar X, preškálujme ho s koeficientom d. Nech N(d) je počet takýchto preškálovaných objektov, ktoré treba na úplné pokrytie pôvodného objektu. Potom je fraktálna (Hausdorffova) dimenzia definovaná takto: · Majme úsečku. Preškálujme ju napr. s koeficientom 1/3, čím dostaneme úsečku tretinovej dĺžky. Na pokrytie pôvodnej úsečky potrebujeme tri tieto menšie úsečky. Ak preškálujeme úsečku s koeficientom 1/4, budeme na pokrytie pôvodnej úsečky potrebovať štyri menšie úsečky atď. Preto platí: · Fraktálna dimenzia úsečky je teda rovná jej topologickej dimenzii, teda 1.

Fraktálna dimenzia · Teraz majme trojuholník. Preškálujme ho s koeficientom 1/2. Na pokrytie pôvodného trojuholníka budeme potrebovať štyri tieto menšie trojuholníky. Ak preškálujeme trojuholník s koeficientom 1/4, budeme potrebovať na pokrytie pôvodného trojuholníka 16 menších trojuholníkov. Fraktálna dimenzia trojuholníka je teda: · Aj trojuholník má teda fraktálnu dimenziu rovnú svojej topologickej dimenzii. Takýto výsledok je typický pre útvary, ktoré nie sú fraktálmi.

Fraktálna dimenzia · Teraz vypočítajme fraktálnu dimeziu spomenutých fraktálov. · 1. Pre Cantorovo diskontinuum dostávame, že ak preškálujeme pôvodný útvar s koeficientom 1/3, stačia nám na jeho pokrytie dva preškálované útvary. Ak preškálujeme s koeficientom 1/9, budeme potrebovať 4 menšie útvary atď. Máme teda: Topologická dimenzia Cantorovho diskontinua je 0, pretože sa skladá len z bodov. Fraktálna dimenzia je však väčšia. · 2. Pre Kochovej krivku platí, že ak preškálujeme krivku s koeficientom 1/3, potrebujeme na pokrytie pôvodnej krivky 4 preškálované krivky. Ak preškálujeme krivku s koeficientom 1/9, potrebujeme na pokrytie pôvodnej krivky 16 preškálovaných kriviek. Dostávame: Tento rozmer je opäť väčší ako topologická dimenzia krivky, ktorá je 1.

Fraktálna dimenzia · 3. Pre Sierpinského trojuholník dostaneme podobný výsledok. Ak preškálujeme trojuholník s koeficientom 1/2, na pokrytie pôvodného útvaru potrebujeme 3 menšie trojuholníky. Ak preškálujeme s koeficientom 1/4, budeme potrebovať 9 menších trojuholníkov. Máme: Po nekonečnom počte vyňatí stredných trojuholníkov bude Sierpinského trojuholník len nekonečnou sieťou čiar. Jeho plocha je nulová, topologická dimenzia je 1. · Tieto výsledky môžeme zhrnúť do nasledujúceho poznatku – fraktály sú útvary, ktorých fraktálna dimenzia je vyššia ako ich topologická dimenzia.

Fraktálna dimenzia · Je možné odhadnúť fraktálnu dimenziu niektorých prírodných útvarov, čo potvrdzuje ich fraktálny charakter: pobrežie: 1. 26 povrch mozgu človeka: 2. 76 povrch skaly: 2. 2 obvod 2 D rezu oblaku: 1. 33

IFS · IFS (iterated function systems), alebo systémy iterovaných funkcií, sú podmnožinou lineárnych deterministických fraktálov. · Základom je definovanie niekoľkých transformácií, ktoré sa postupne aplikujú na bod. · Majme množinu transformácií 1. . . n. Zvoľme si bod X. Potom bod X’= i 1( i 2( i 3(. . . im(X). . . ))) kde m a i 1. . . im {1. . . n} je bodom fraktálu typu IFS. Jeden bod fraktálu typu IFS teda dostaneme tak, že na nejaký bod nekonečne veľakrát aplikujeme zvolené transformácie, a to v náhodnom poradí, opakovanie je možné. Náhodný výber transformácií prebieha tak, že transformáciu i vyberieme s pravdepodobnosťou pi. Aby sme dostali všetky body fraktálu, musíme tento postup opakovať nekonečne veľakrát. · Transformácie i nemôžu byť ľubovoľné, ale musia spĺňať isté podmienky: · 1. Musia to byť afinné transformácie, t. j. transformácie typu: (X)=AX+B kde X je bod, A matica a B vektor. Teda sú to napr. klasické transformácie otočenia, posunutia a škálovania a ich rôzne kombinácie.

IFS · 2. Každá z týchto transformácií v sebe môže obsahovať aj operáciu škálovania. Nech transformácia i je vybraná s pravdepodobnosťou pi a má koeficient škálovania si (ak si<1, ide o zmenšenie, ak si>1, ide o zväčšenie). Musí platiť tzv. podmienka priemernej kontrakcie, teda: s 1 p 1. s 2 p 2. s 3 p 3. . . snpn<1 pričom platí: Táto podmienka hovorí o tom, že v priemere by mala byť vzdialenosť dvoch transformovaných bodov menšia ako vzdialenosť pôvodných dvoch bodov. · Fraktály IFS sa vyznačujú tým, že majú svoj atraktor – to je množina, ktorá obsahuje všetky body vygenerované pomocou daných transformácií s danými pravdepodobnosťami. Množina sa nazýva atraktorom preto, lebo “priťahuje” všetky body, ktoré vzniknú postupným aplikovaním transformácií, bez ohľadu na to, s akým bodom sa začalo.

IFS Príklad: Sierpinského trojuholník ako atraktor · Už sme si hovorili, ako dostať Sierpinského trojuholník pomocou transformácií: · 1. Preškálovanie, d=0. 5 (X A) · 2. Škálovanie + posunutie v smere x o 1/2 dĺžky podstavy X (X B) · 3. Škálovanie + posunutie v smere x o 1/4 dĺžky podstavy trojuholníka X + posunutie v smere y o 1/2 dĺžky výšky trojuholníka X (X C) C A X B p 1=1/3, p 2=1/3, p 3=1/3 · Nech má trojuholník X podstavu dĺžky 2 a výšku 1. Matematicky zaspíšeme uvedené transformácie takto: 1. x’=0. 5 x y’=0. 5 y 2. x’=0. 5 x+1 y’=0. 5 y 3. x’=0. 5 x+0. 5 y’=0. 5 y+0. 5 · Všetky transformácie robíme s rovnakou pravdepodobnosťou 1/3. Zápis vo forme IFS by teda vyzeral takto:

IFS výsledný bod štartovací bod

IFS · Príklad: Barnsleyho papraď · Pri zostrojovaní takejto paprade postupujeme tak, že najskôr zostrojíme stopku po prvý list vľavo, potom prvý list vľavo a vpravo a potom celú túto časť zmenšíme a pootočíme, čím vytvoríme ďalšie poschodie paprade. · Predpokladajme, že papraď má výšku 10. Budeme potrebovať 4 transformácie: · 1. Transformácia, ktorá prevedie ľubovoľný bod na bod prvého úseku stopky. Prvý úsek stopky je zvislý a má dĺžku 1/6 z celkovej výšky, začína v bode (0, 0). Preto má transformácia nasledujúci tvar: x’=0 y’=0. 16 y

IFS · 2. Transformácia, ktorá transformuje celú papraď do spodného ľavého listu. Táto transformácia sa skladá z viacerých transformácií: · Škálovanie – s koeficientom 0. 3 v smere x, 0. 34 v smere y · Otočenie proti smeru hodinových ručičiek o 49° · Posunutie v smere y o 1/6 výšky, t. j. 1. 6 Transformáciu zapíšeme takto: x’=0. 20 x - 0. 26 y y’=0. 23 x + 0. 22 y + 1. 6

IFS · 3. Transformácia, ktorá transformuje celú papraď do spodného pravého listu. Táto transformácia sa skladá z týchto transformácií: · Preklopenie podľa osi y · Škálovanie – s koeficientom 0. 3 v smere x, 0. 37 v smere y · Skosenie v smere y s koeficientom -0. 19 · Otočenie v smere hodinových ručičiek o 50° · Posunutie v smere y o 0. 44 Matematický zápis vyzerá takto: x’=-0. 15 x + 0. 28 y y’=0. 26 x + 0. 24 y + 0. 44

IFS · 4. Transformácia, ktorá transformuje dolné poschodie paprade na nasledujúce poschodie. Táto transformácia je zložená z týchto zobrazení: · Škálovanie s koeficientom 0. 85 v smere x aj y · Otočenie v smere hodinových ručičiek o 2. 5° · Posunutie v smere y o 1. 6 x’=0. 85 x + 0. 04 y y’=-0. 04 x + 0. 85 y + 1. 6 · Pri tomto fraktále majú jednotlivé transformácie rôzne pravdepodobnosti. Platí: p 1=0. 01 p 2=0. 07 p 3=0. 07 p 4=0. 85

IFS · Majme teda dané transformácie 1. . . n a pravdepodobnosti p 1. . . pn. Chceme vykresliť príslušný fraktál IFS. Budeme ho vykresľovať po bodoch. Čím viac bodov vykreslíme, tým bude útvar úplnejší. Čím viac iterácií aplikovania transformácií i urobíme, tým bude bod bližšie k aktraktoru. Algoritmus generovania IFS môžeme zapísať takto: · · Zvoľ počet bodov n, ktoré sa majú vygenerovať Zvoľ počet iterácií m Zvoľ počiatočný bod (x. P, y. P) Opakuj pre i=1. . . n · P= (x. P, y. P) · Opakuj pre j=1. . . m · Náhodne vyber zobrazenie j s príslušnou pravdepodobnosťou · P= j(P) · Vykresli bod P

IFS a korytnačia grafika · Korytnačia grafika je spôsob kreslenia, keď sa v obrázku pohybuje pomyselný objekt (“korytnačka”) a pri pohybe môže za sebou zanechávať čiaru. Pohyb korytnačky riadime tým, že jej udáme smer pohybu a dĺžku, o akú sa má v tomto smere posunúť.

IFS a korytnačia grafika Príklad: Strom vykreslený korytnačou grafikou · Chceme vykresliť nasledujúci strom: · Postupujeme takto: · 1. Na začiatku sa korytnačka pohybuje v smere vektora v=(0, 1) (teda nahor) a dĺžka kmeňa stromu je d. · 2. Nakreslíme kmeň · 3. Korytnačka si náhodne vyberie, či otočí smer pohybu v o 30° v smere hodinových ručičiek alebo proti smeru HR · 4. d sa skráti na polovicu · 5. Nakreslíme čiaru v smere v s dĺžkou d · 6. Vrátime sa do bodu 3 Tento postup po istom počte krokov zastavíme. · Takto získame jednu vetvu stromu (na obrázku vyznačenú červenou). Vrátime sa ku koreňu a celý postup opakujeme, kým nie je strom dostatočne hustý.

IFS a korytnačia grafika · Algoritmus pre tento strom môžeme zapísať takto: · · Zvoľ počet opakovaní n (počet vetiev) Zvoľ počet krokov v rámci jednej vetvy m Zvoľ dĺžku kmeňa d Opakuj pre i=1. . . n · v=(0, 1), x=d · Opakuj pre j=1. . . m · Vykresli čiaru v smere v s dĺžkou x · Náhodne vyber jedno z čísel 1, 2 · Ak je vybratá 1, tak otoč v o 30° v smere HR · Ak je vybratá 2, tak otoč v o 30° proti smeru HR · x=x/2

Štatistické fraktály Metóda náhodného presúvania stredného bodu · Pomocou tejto metódy získame náhodne vyzerajúce útvary, ktoré sa v praxi môžu použiť napr. na modelovanie hôr alebo pobrežia.

Štatistické fraktály · Postup metódy náhodného presúvania stredného bodu v 1 D je nasledujúci: · 1. Začíname s dvomi bodmi A, B so súradnicami (x. A, y. A), (x. B, y. B). · 2. Nájdeme stred úsečky AB, označíme ho C, jeho súradnice sú (x C, y. C). · 3. Vygenerujeme náhodné číslo d a pripočítame ho k y. C. Bod C má teda súradnice (x. C, y. C+d)=((x. A+x. B)/2, (y. A+y. B)/2+d) · 4. Nájdeme stred úsečky AC, označíme ho D, jeho súradnice sú (x D, y. D) · 5. Vygenerujeme náhodné číslo d a pripočítame ho k y. D. Bod D má teda súradnice (x. D, y. D+d). · 6. Nájdeme stred úsečky CB, označíme ho E, jeho súradnice sú (x E, y. E) · 7. Vygenerujeme náhodné číslo d a pripočítame ho k y. E. Bod E má teda súradnice (x. E, y. E+d). · 8. Postup opakujeme pre všetky novovzniknuté úsečky C B A A D B A C E B

Štatistické fraktály · Náhodné čísla, ktoré v tomto algoritme generujeme, nemôžu byť ľubovoľné, ale musia mať Gaussovské rozloženie. Funkcia hustoty pre takéto rozloženie je daná ako: · Pre náš algoritmus potrebujeme náhodné čísla so strednou hodnotou =0. Smerodajná odchýlka je na začiatku rovná 1. V i-tom kroku (zjemnení) platí: · Koeficient H sa nazýva Hurstov exponent.

Mandelbrotova množina · Mandelbrotova množina je špeciálna množina komplexných čísel, ktorej hranicou je fraktál. · Množina je daná nasledujúcim predpisom: M={c C; xn+1=xn 2+c< n N; x 0=0} Je to teda množina komplexných čísel c, pre ktoré opakovaným aplikovaním iteračného predpisu xn+1=xn 2+c, kde x 0=0, dostávame konečné komplexné čísla (presnejšie povedané čísla s konečnou absolútnou hodnotou). · Napr. pre c=1 dostávame x 0=0, x 1=1, x 2=2, x 3=5, x 4=26. . . 1 M · Pre c=i dostaneme x 0=0, x 1=i, x 2=-1+i, x 3=-i, x 4=-1+i. . . i M

Juliova množina · Juliova množina je definovaná podobným spôsobom ako Mandelbrotova. Máme: J={x 0 C; xn+1=xn 2+c< n N} kde c je daná konštanta. · Pre rôzne konštanty c dostávame rôzne útvary: c=-0. 618 c=-0. 70176 -0. 3842 i c=-0. 4+0. 6 i c=0. 285+0. 01 i c=-0. 835 -0. 2321 i

Systémy častíc · Systémy častíc sa používajú pri modelovaní zložitých objektov, ktoré sa v čase menia a ťažko sa reprezentujú pomocou plôch – napr. dym, oheň, hmla, voda, sneh, tráva, kŕdeľ vtákov a pod.

Systémy častíc · Systém častíc sa obyčajne skladá z veľkého množstva menších podobných objektov (body, kvapky, vločky, guličky a pod. ). Každý objekt je daný rôznymi charakteristikami (farba, veľkosť, rýchlosť, smer pohybu, pružnosť atď. ). Každá charakteristika systému má nejakú strednú hodnotu. Zadá sa táto hodnota a pre každú časticu sa potom určí jej charakteristika vzťahom: x=Sx+d kde Sx je stredná hodnota veličiny x a d je náhodné číslo. · Charakteristiky jednotlivých častíc a celého systému sa v čase menia. · Správanie sa systému častíc v čase môžeme opísať takto: · 1. Ak je v scéne nejaké miesto vzniku častíc, vytvoria sa nové častice · 2. Pre každú novú časticu sa určia jej charakteristiky · 3. Na základe charakteristík častíc, prípadne vonkajších vplyvov sa určí aktuálny stav (poloha, rýchlosť, veľkosť) danej častice · 4. Ak niektorá častica opustí scénu (alebo iný vymedzený priestor) alebo skončí doba jej životnosti, zaniká · 5. Zobrazia sa všetky existujúce častice

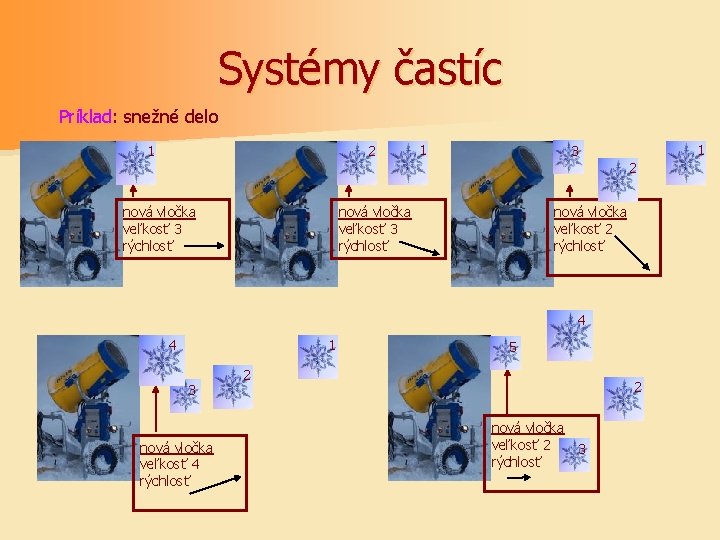
Systémy častíc Príklad: snežné delo 1 2 1 1 3 2 nová vločka veľkosť 3 rýchlosť nová vločka veľkosť 2 rýchlosť 4 1 4 3 nová vločka veľkosť 4 rýchlosť 5 2 2 nová vločka veľkosť 2 3 rýchlosť