Floating Point Representation and Arithmetic see Patterson Chapter

Floating Point Representation and Arithmetic (see Patterson Chapter 4) 1

Outline • • • Review of floating point scientific notation Floating point binary IEEE Floating Point Standard Addition in Floating Point Remarks about multiplication 2

Floating Point Notation • Decimal • 12. 4568 ten (decimal notation) means • • 10*1 + 2 + 4/10 + 5/100 + 6/1000 + 8/10000 In scientific notation • 12. 4568 = • • • 124568 * 10 -4 = 1245680 * 10 -5 = 12456. 8 * 10 -3 = 1245. 68 * 10 -2 = 124. 568 * 10 -1 =12. 4568 * 100 1. 24568 * 101 1. 24568*101 is an example of normalised scientific notation. 3

Floating Point in Binary • 0. 010011 two = (0/2) + (1/22) + (0/24) +(1/25) + (1/26) • • 0 + 1/4 + 0 + 1/32 + 1/64 = (0. 25 + 0. 03125 + 0. 015625)ten = 0. 296875 ten In scientific notation • = = 10011*2 -6 = 1001. 1*2 -5 = 100. 11*2 -4 1. 0011*2 -2 normalised 4

Normalised Notation • In normalised binary scientific notation • unless the number is 0 • • always have 1. sssssss. . . sss * 2 E sss. . . sss is the significand E is the exponent The significand s 1 s 2. . . sn represents 5

Representation • • Note that it is impossible to exactly represent all decimal numbers in this way (eg 0. 3) Problem of representation of floating point numbers in fixed word length • need to represent • • significand exponent in one word (32 bits). 6

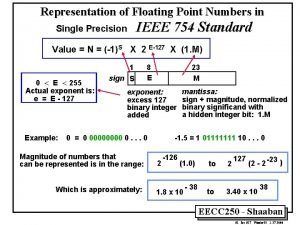
Representation 31 30 23 22 sign bit exponent significand: 23 bits F S 8 bits E • 0 Represents floating point number: • • (-1)S * (1. 0+F) * 2 E S is 1 bit (if S=1 then negative) F is 23 bits E is 8 bits 7

Squeezing out More from the Bits • Since every non-zero binary f. p. number (normalised) is of the form: • • We do not have to represent explicitly the 1 in the word, and can therefore interpret the bitpattern as: • • • 1. sss. . . sss *2 E (-1)S (1 + significand) * 2 E thus ‘reclaiming’ an extra bit! E= 0000 is reserved for zero. 8

Requirements • • As far as possible the ALU should be able to reuse integer machinery in implementation of f. p. Eg, comparison with zero • easy because of sign bit • • fp numbers can be easily classified as negative, zero or positive without additional hardware. Comparison of two fp numbers x<y not so straightforward • how are negative exponents to be formed? 9

Bad Example: (1/2) > 2 ? ? ? • Representation of 1/2 is • l 0. 1 two = 1. 0*2 -1 (normalised) 0 1111 S E 0000. . 0000 significand Representation of 2 is » 10 two = 1. 0*21 (normalised) 0 0001 S E 0000. . 0000 significand 10

Representation of Exponent • Inappropriate to use two’s complement for the exponent • • Ideally want 0000 to represent most negative number, 1111 most positive. Number range: 0111 1111 = 127 ten 1111 positive 1111 1110. . . . use this for 20 0111 1111 0111 1110. . . negative 0000 11

Biased Representation (IEEE FP Standard) • • • The ‘bias’ 127 represents 0 128 to 255 represent positive exponents 1 to 127 represent negative exponents • • The actual exponent is therefore: • • (remember 0 is reserved for the entire number being zero). E - bias (-1)S * (1 + significand) * 2 E-bias 12

Example 1 • • Represent 0. 3125 ten = 5/16 = 1/4 + 1/16 = 0. 0101 two = 1. 01*2 -2 S=0 E = ? ? ? • -2 = E-bias • E = 125 ten = E-127 = 0111 1101 two • Significand = 010. … 000 • 0 0111 1101 010000. . . 000 13

Example 2 • What does • • • 010000. . . 000 S=0 E = 0111 1101 = 125 ten • • 0 0111 1101 represent? Exponent = E-bias = 125 -127 = -2 Significand = 1/4 (-1)S(1+sig. )2 E-bias = (1 + 1/4)*(1/4) = 5/16 14

Addition of FP Numbers • Given two numbers: • • • normalise them both adjust the floating point of the smaller number to match the larger one Add them together renormalise check for underflow/overflow of exponent • • if so then break; round significand to required number of bits • might need renormalisation (eg, 11111 round to 4 bits). 15

Addition Example • 0. 5 + 2. 75 = 3. 25 • 0. 1 two + 10. 11 two • 1. 0*2 -1 + 1. 011*21 • 0. 010*21 + 1. 011*21 • 1. 101*21 (already normalised) • (1 + (1/2) + (1/8)) * 2 • 3. 25 16

Remarks • • • The IEEE FP standard represents floats in 32 bits, higher precision represented across two words (doubles). Multiplication is relatively easy, since the exponents add, and the significands can be done with integer multiplication. There can be huge pitfalls in reliably transferring floating point code to different hardware! 17

Summary • • • FP scientific notation normalised representation in binary Bias to represent -ve to +ve range in exponent Addition Notice how a 32 -bit binary string can represent many different entities in memory. Memory architectures NEXT. 18