IEEE Floating Point The IEEE Floating Point Standard

Lecture overview o o o The standard Floating Point Basics A floating point adder

The floating point standard o Single Precision o Value of bits stored in representation

The floating point standard o Double Precision o Value of bits in word representation

The floating point standard o Notes on single and double precision n The leading

Conversion Examples o Converting from base 10 to the representation Single precision example Covert

Conversion Example Continued o o 1. 1001 x 26 is binary for 100 Thus

Another example o Representation for -175 (sign magnitude rep) n n n n 175

$A fractional example o o o o Decimal value 0. 25 Convert to binary$

Converting back o o Convert $C 32 F 0000 into decimal Extract components from

Another example o Convert $41 C 8 0000 to decimal n n n 0100

Arithmetic with floating point numbers o o Add op 1 $42 C 8 0000

Now add the mantissas o But first align the mantissas n n n Op

Add op 1 mantissa with the aligned op 2 mantissa n n n o

Constructing Result Value o Sign 0 Exponent 6 E = 1000 0101 = 133

Floating point representation of 125 o o o Positive so s is 0 Exponent

Multiplication example o o Multiply op 1 $42 C 8 0000 & op 2

Multiplication basics o Base 10 example n o o o 3 x 102 *

So here o o Have sign of both is + so result is +

The mantissas o Do a binary multiplication n n n o 1. 1001 1100

Final result o o o Exponent is 137 or 10 Mantissa is 10. 01110001

Specification of a FPA o o Floating Point Add/Subtract Unit Specification n Inputs in

Specifications continued n n Result will be a IEEE 754 Double Precision representation Unit

Specifications continued o Outputs n n The correctly represented result Flags that are output

High level block diagram o Basic architecture interface n n Data – 64 bit

Start the VHDL o The entity interface o In the next lecture 1/8/2007 -

Denormalized Example o Denormalized example(multiplication by 100) n n n o $0010 0000 is

Do multiplication o Had the FP representation of 100 n n n o S=0

Renormalize o The values to store n n o S=0 -121 E=2 for a

Slides: 29

Download presentation

The floating point standard o Single Precision o Value of bits stored in representation is: n n If e=255 and f /= 0, then v is Na. N regardless of s s If e=255 and f = 0, then v = (-1) ¥ s If 0 < e < 255, then v = (-1) 2 e-127 (1. f) – normalized number s If e = 0 and f /= 0, the v = (-1) 2 -126 (0. f) o n Denormalized numbers – allow for graceful underflow s If e = 0 and f = 0 the v = (-1) 0 (zero) 1/8/2007 - L 24 IEEE Floating Point Basics Copyright 2006 - Joanne De. Groat, ECE, OSU 3

The floating point standard o Double Precision o Value of bits in word representation is: n n n If e=2047 and f /= 0, then v is Na. N regardless of s s If e=2047 and f = 0, then v = (-1) ¥ s e-1023 If 0 < e < 2047, then v = (-1) 2 (1. f) o n s If e = 0 and f /= 0, the v = (-1) 2 -1022 (0. f) o n – normalized number Denormalized numbers – allow for graceful underflow s If e = 0 and f = 0 the v = (-1) 0 (zero) 1/8/2007 - L 24 IEEE Floating Point Basics Copyright 2006 - Joanne De. Groat, ECE, OSU 4

The floating point standard o Notes on single and double precision n The leading 1 of the fractional part is not stored for normalized numbers o n n Mantissa 1. 001001001…. Representation allows for +0 and -0 indicating direction of 0 (allow determination that might matter if rounding was used) Denormalized numbers allow graceful underflow towards 0 1/8/2007 - L 24 IEEE Floating Point Basics Copyright 2006 - Joanne De. Groat, ECE, OSU 5

Conversion Examples o Converting from base 10 to the representation Single precision example Covert 10010 Step 1 – convert to binary - 0110 0100 o In a binary representation form of 1. xxx have o o o n 0110 0100 = 1. 100100 x 26 1/8/2007 - L 24 IEEE Floating Point Basics Copyright 2006 - Joanne De. Groat, ECE, OSU 6

Conversion Example Continued o o 1. 1001 x 26 is binary for 100 Thus the exponent is a 6 n n n o Biased exponent will be 6+127=133 = 1000 0101 Sign will be a 0 for positive Stored fractional part f will be 1001 Thus we have n n se f 0 100 0 010 1 1 00 1000…. 4 2 C 8 0 0 in hexadecimal $42 C 8 0000 is representation for 100 1/8/2007 - L 24 IEEE Floating Point Basics Copyright 2006 - Joanne De. Groat, ECE, OSU 7

Another example o Representation for -175 (sign magnitude rep) n n n n 175 = 128 + 32 + 8 + 4 + 2 +1 = 1010 1111 Or 1. 0101111 x 27 S=1 Exponent is 7 +127 = 134 = 1000 0110 Fractional part f = 0101111 Representation 1100 0011 0010 1111 0000 …. Or in Hex $C 32 F 0000 1/8/2007 - L 24 IEEE Floating Point Basics Copyright 2006 - Joanne De. Groat, ECE, OSU 8

$A fractional example o o o o Decimal value 0. 25 Convert to binary$

A fractional example o o o o Decimal value 0. 25 Convert to binary 0. 0100 In power form 1. 0000 x 2 -2 Sign is + so 0 Exponent is -2 +127 = 125 = 0111 1101 Fractional part is 00000… Representation is 0 011 1110 1 0000 … And in Hex $3 E 80 0000 1/8/2007 - L 24 IEEE Floating Point Basics Copyright 2006 - Joanne De. Groat, ECE, OSU 9

Converting back o o Convert $C 32 F 0000 into decimal Extract components from n n n n 1100 0011 0010 1111 S=1 Exponent = 1000 0110 = 128+4+2 = 134 unbias 134 – 127 =7 f = 0101111 so mantissa is 1. 0101111 Adjust man by exponent 1010 1111 (move binary pt 7 places) Or 128+32+15 = 175 Sign is negative so -175 1/8/2007 - L 24 IEEE Floating Point Basics Copyright 2006 - Joanne De. Groat, ECE, OSU 10

Another example o Convert $41 C 8 0000 to decimal n n n 0100 0001 1100 1000 0000 …. S is 0 so positive number Exponent 1000 0011 = 128+3=131 -127=4 f = 1001 so mantissa is 1. 1001 With 4 binary positions have 11001 as final number in binay which is 25 1/8/2007 - L 24 IEEE Floating Point Basics Copyright 2006 - Joanne De. Groat, ECE, OSU 11

Arithmetic with floating point numbers o o Add op 1 $42 C 8 0000 and op 2 $41 C 8 0000 First divide into component parts n Op 1 $42 C 8 0000 =0100 0010 1100 1000 0000 …. o o o n S=0 E = 1000 0101 = 133 – 127 = 6 Mop 1 = 1. 10010000… Op 2 $41 C 8 0000 =0100 0001 1100 1000 0000 …. o o o 1/8/2007 - L 24 IEEE Floating Point Basics S=0 E = 1000 0011 = 131 – 127 = 4 Mop 2 = 1. 10010000… Copyright 2006 - Joanne De. Groat, ECE, OSU 12

Now add the mantissas o But first align the mantissas n n n Op 1 1. 1001000…. Op 2 1. 1001000…. Which is the smaller number and needs to be aligned Exponent difference between op 1 and op 2 is 2 So shift op 2 by 2 binary places or Op 2 becomes 0. 0110010000… 1/8/2007 - L 24 IEEE Floating Point Basics Copyright 2006 - Joanne De. Groat, ECE, OSU 13

Add op 1 mantissa with the aligned op 2 mantissa n n n o o o 1. 1001000000… 0. 0110010000… 1. 1111010000 Result exponent is 6 Value is 1111101 or 64+32+16+8+4+1=125 Values added were 100 and 25 1/8/2007 - L 24 IEEE Floating Point Basics Copyright 2006 - Joanne De. Groat, ECE, OSU 14

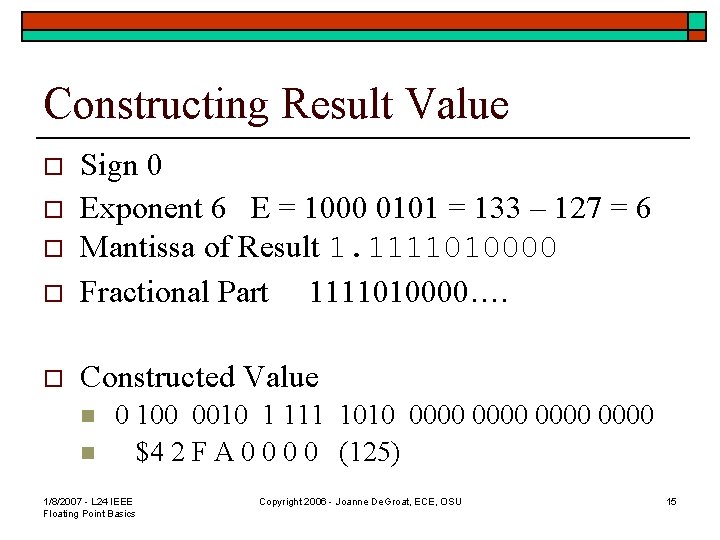
Constructing Result Value o Sign 0 Exponent 6 E = 1000 0101 = 133 – 127 = 6 Mantissa of Result 1. 1111010000 Fractional Part 1111010000…. o Constructed Value o o o n n 0 100 0010 1 111 1010 0000 $4 2 F A 0 0 (125) 1/8/2007 - L 24 IEEE Floating Point Basics Copyright 2006 - Joanne De. Groat, ECE, OSU 15

Floating point representation of 125 o o o Positive so s is 0 Exponent is 6 + 127 = 133 = 1000 0101 Fractional part from mantissa of n o 1. 111101 or 111101 Constructed value n n 0 1000 0101 111101 000000000 $42 FA 0000 1/8/2007 - L 24 IEEE Floating Point Basics Copyright 2006 - Joanne De. Groat, ECE, OSU 16

Multiplication example o o Multiply op 1 $42 C 8 0000 & op 2 $41 C 8 0000 First divide into component parts n Op 1 $42 C 8 0000 =0100 0010 1100 1000 0000 …. o o o n S=0 E = 1000 0101 = 133 – 127 = 6 Mop 1 = 1. 10010000… Op 2 $41 C 8 0000 =0100 0001 1100 1000 0000 …. o o o 1/8/2007 - L 24 IEEE Floating Point Basics S=0 E = 1000 0011 = 131 – 127 = 4 Mop 2 = 1. 10010000… Copyright 2006 - Joanne De. Groat, ECE, OSU 17

Multiplication basics o Base 10 example n o o o 3 x 102 * 1. 1 x 102 = 3. 3 x 104 Have 2 numbers A x 2 ea and B x 2 eb Multiply and get result = A*B x 2 ea+eb 1/8/2007 - L 24 IEEE Floating Point Basics Copyright 2006 - Joanne De. Groat, ECE, OSU 18

So here o o Have sign of both is + so result is + Exponent addition n n Both exponents are biased as stored If you add stored binary exponents you need to subtract the extra bias or 127 Or using pencil and paper (or powerpoint) can just add the unbiased exponent of one operand to the other biased exponent Here have 133 + 4 = 137 = 1000 1001 1/8/2007 - L 24 IEEE Floating Point Basics Copyright 2006 - Joanne De. Groat, ECE, OSU 19

The mantissas o Do a binary multiplication n n n o 1. 1001 1100 1 1100111 0001 and add Adjusting for binary point have 10. 01110001 1/8/2007 - L 24 IEEE Floating Point Basics Copyright 2006 - Joanne De. Groat, ECE, OSU 20

Final result o o o Exponent is 137 or 10 Mantissa is 10. 01110001 Adjusted for exponent 1001 1100 0100 Value is 2048+256+128+64+4 Or 2304+128+68 = 2432 + 68 = 2500 And we were multiplying 100 * 25 1/8/2007 - L 24 IEEE Floating Point Basics Copyright 2006 - Joanne De. Groat, ECE, OSU 21

Specification of a FPA o o Floating Point Add/Subtract Unit Specification n Inputs in IEEE 754 Double Precision Must perform both addition and subtraction Must handle the full floating point standard o o 1/8/2007 - L 24 IEEE Floating Point Basics Normalized numbers Not a Numbers – Na. Ns +/- Infinity Denormalized numbers Copyright 2006 - Joanne De. Groat, ECE, OSU 22

Specifications continued n n Result will be a IEEE 754 Double Precision representation Unit will correctly handle the invalid operation of adding + ¥ and - ¥ = Nan per the standard Unit latches it inputs into registers from parallel 64 -bit data busses. There is a separate signal line that indicates the operation add or subtract 1/8/2007 - L 24 IEEE Floating Point Basics Copyright 2006 - Joanne De. Groat, ECE, OSU 23

Specifications continued o Outputs n n The correctly represented result Flags that are output are o o o o 1/8/2007 - L 24 IEEE Floating Point Basics Zero result Overflow to infinity from normalized numbers as inputs Na. N result Overshift (result is the larger of the two operands) Denormalized result Inexact (result was rounded) Invalid operation for addition Copyright 2006 - Joanne De. Groat, ECE, OSU 24

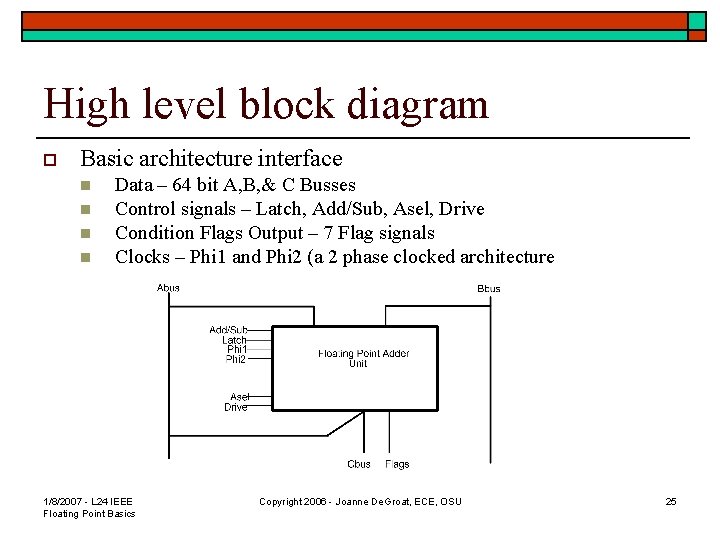
High level block diagram o Basic architecture interface n n Data – 64 bit A, B, & C Busses Control signals – Latch, Add/Sub, Asel, Drive Condition Flags Output – 7 Flag signals Clocks – Phi 1 and Phi 2 (a 2 phase clocked architecture 1/8/2007 - L 24 IEEE Floating Point Basics Copyright 2006 - Joanne De. Groat, ECE, OSU 25

Denormalized Example o Denormalized example(multiplication by 100) n n n o $0010 0000 is 0 0000 0010000…… f =. 001000000 *$42 C 8 0000 (100) Change Denormalized to 2 n n n e-127 form(was 2 e-126 ) S=0 E = 2 -127 M = x. f = 0. 0100 0000 …… 1/8/2007 - L 24 IEEE Floating Point Basics Copyright 2006 - Joanne De. Groat, ECE, OSU 27

Do multiplication o Had the FP representation of 100 n n n o S=0 6 E=2 (133 – 127) M = 1. f = 1. 1001 Multiply and get a result with n n n S=0 E = 26 -127 = -121 M = 1. 1001*0. 01 = 0. 011001 1/8/2007 - L 24 IEEE Floating Point Basics Copyright 2006 - Joanne De. Groat, ECE, OSU 28

Renormalize o The values to store n n o S=0 -121 E=2 for a mantissa of 0. 011001 (stored e 6) Adjust to normailized form -123 E=2 for a mantissa of 001. 1001 (stored e 4) Construct value to store n n S E F 0 0000 0100 1001 0000 ……… = $0248 0000 1/8/2007 - L 24 IEEE Floating Point Basics Copyright 2006 - Joanne De. Groat, ECE, OSU 29