Engineering Economy Chapter 3 The Time Value of









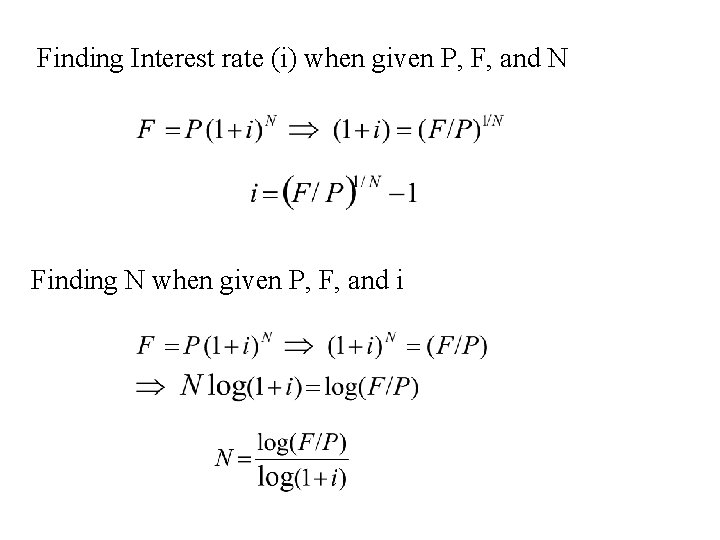
















- Slides: 34

Engineering Economy Chapter 3: The Time Value of Money The objective of Chapter 3 is to explain time value of money calculations and to illustrate economic equivalence.

Money has a time value. • Capital refers to wealth in the form of money or property that can be used to produce more wealth. • Engineering economy studies involve the commitment of capital for extended periods of time.

Simple Interest: infrequently used When the total interest earned or charged is linearly proportional to the initial amount of the loan (principal), the interest rate, and the number of interest periods, the interest and interest rate are said to be simple.

Computation of simple interest The total interest, I, earned or paid may be computed using the formula below. P = principal amount lent or borrowed N = number of interest periods (e. g. , years) i = interest rate per interest period The total amount repaid at the end of N interest periods is P + I.

Example: If $5, 000 were loaned for five years at a simple interest rate of 7% per year, the interest earned would be So, the total amount repaid at the end of five years would be the original amount ($5, 000) plus the interest ($1, 750), or $6, 750.

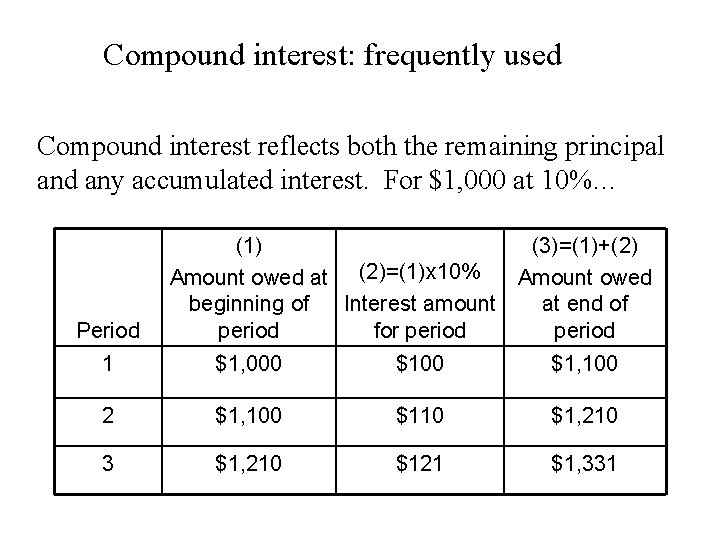
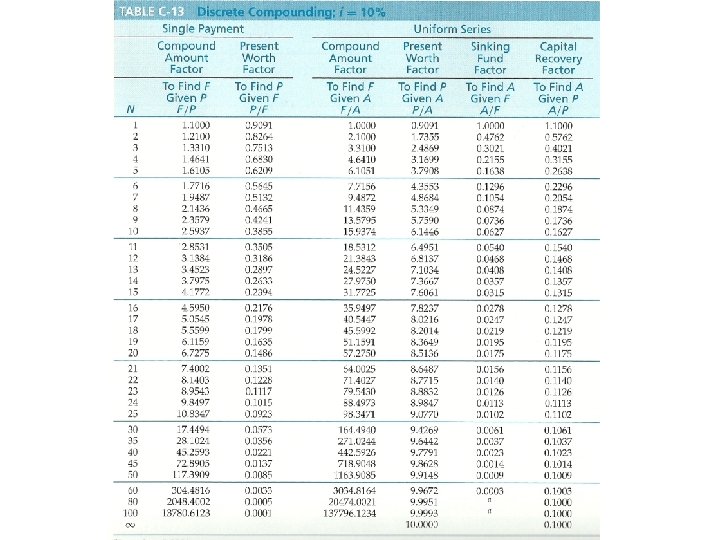
Compound interest: frequently used Compound interest reflects both the remaining principal and any accumulated interest. For $1, 000 at 10%… Period (1) (3)=(1)+(2) Amount owed at (2)=(1)x 10% Amount owed Interest amount beginning of at end of period for period 1 $1, 000 $1, 100 2 $1, 100 $110 $1, 210 3 $1, 210 $121 $1, 331

Notation used in formulas for compound interest calculations. i = effective interest rate per interest period N = number of compounding (interest) periods P = present sum of money; equivalent value of one or more cash flows at a reference point in time; the present F = future sum of money; equivalent value of one or more cash flows at a reference point in time; the future A = end-of-period cash flows in a uniform series continuing for a certain number of periods, starting at the end of the first period and continuing through the last

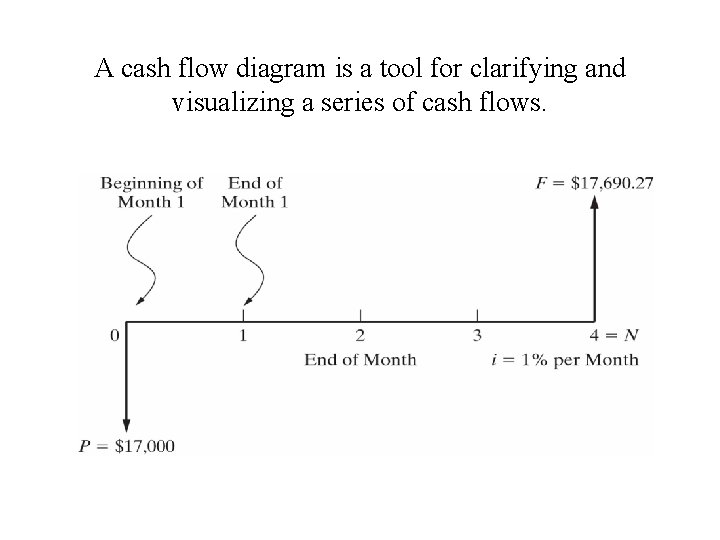
A cash flow diagram is a tool for clarifying and visualizing a series of cash flows.


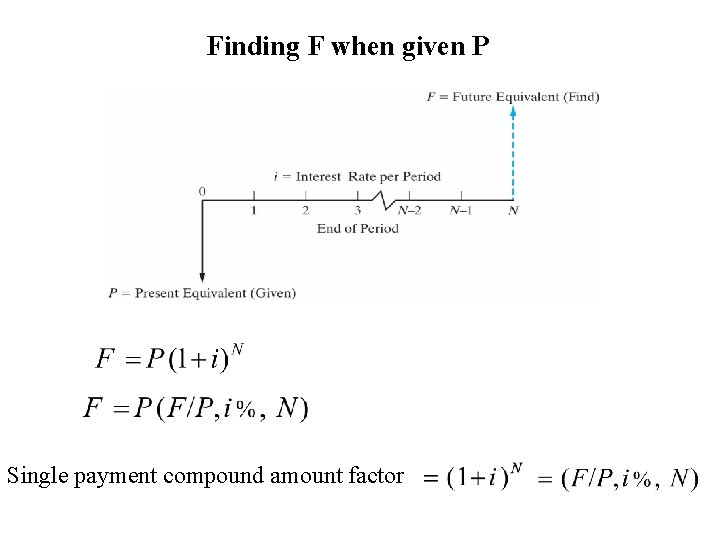
Finding F when given P Single payment compound amount factor



Finding P when given F From Single payment present worth factor

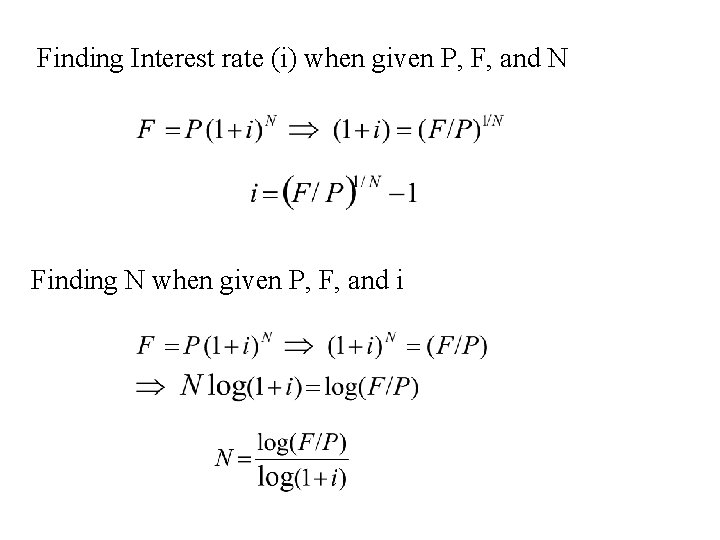
Finding Interest rate (i) when given P, F, and N Finding N when given P, F, and i



Interpolation Example: suppose you wish to have 100, 000$ after 27 years, what amount should be deposited now to provide for it at 7% interest rate per year. 25 27 30 0. 1842 x 0. 1314

Example: suppose you wish to have 100, 000$ after 27 years, what amount should be deposited now to provide for it at 7% interest rate per year.

Interpolation Example: suppose you wish to have 100, 000$ after 20 years, what amount should be deposited now to provide for it at 5. 5% interest rate per year. 5 5. 5 6 0. 3769 x 0. 3118

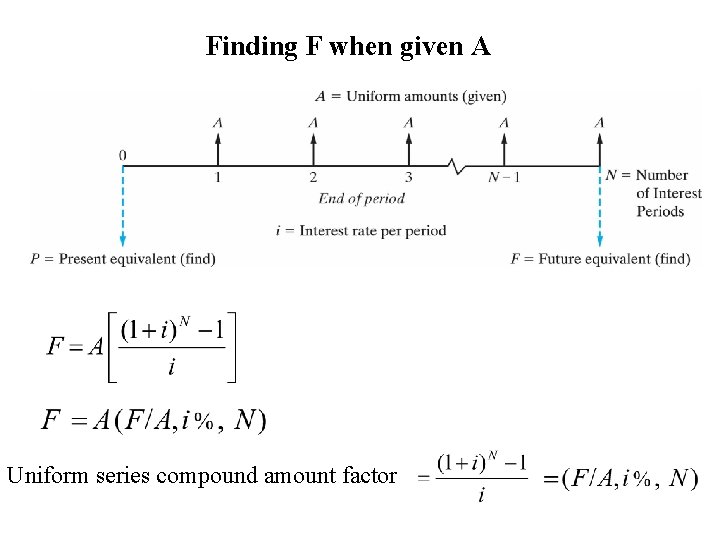
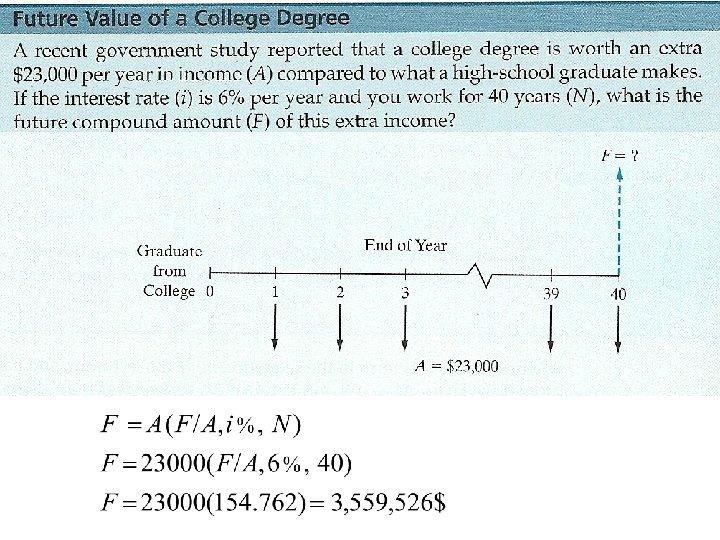
Finding F when given A Uniform series compound amount factor


Finding P when given A Uniform series present worth factor


Finding A when given F Uniform series sinking fund factor

Example: What uniform annual amount should be deposited each year in order to accumulate 2143. 6$ at the time of the eighth annual deposit given i = 10%

Finding A when given P Uniform series capital recovery factor


Finding The number of cash flows in an annuity (N) 1. Given A, P, and i 2. Given A, F, and i

10, 000$ for 20 years 21 th payment equivalents to 1819$ (100, 000 -98, 181) in present


Finding The interest rate (i) given A, N, and F or P Can’t be solved for i

Finding The interest rate (i) given A, N, and F or P

Linear Interpolation i 6% 9. 8975 i 7% 10 10. 2598 i = 6. 28%