Energy of the Simple Harmonic Oscillator The Total













- Slides: 18

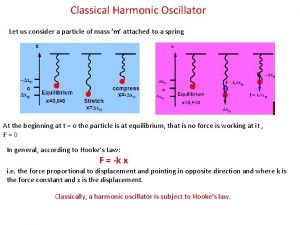
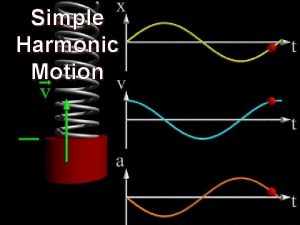
Energy of the Simple Harmonic Oscillator

The Total Mechanical Energy (PE + KE) Is Constant KINETIC ENERGY: • KE = ½ mv 2 • Remember v = -ωAsin(ωt+ϕ) • KE = ½ mω2 A 2 sin 2(ωt+ϕ)

The Total Mechanical Energy (PE + KE) Is Constant POTENTIAL ENERGY: • PE = ½ kx 2 • Remember x = Acos(ωt+ϕ) • PE = ½ k. A 2 cos 2(ωt+ϕ)

The Total Mechanical Energy (PE + KE) Is Constant Etot = KE + PE • Etot = ½k. A 2(sin 2(ωt+ϕ) + cos 2(ωt+ϕ)) • Remember: • ω2 = k/m • sin 2θ + cos 2θ = 1 • Therefore Etot = ½k. A 2

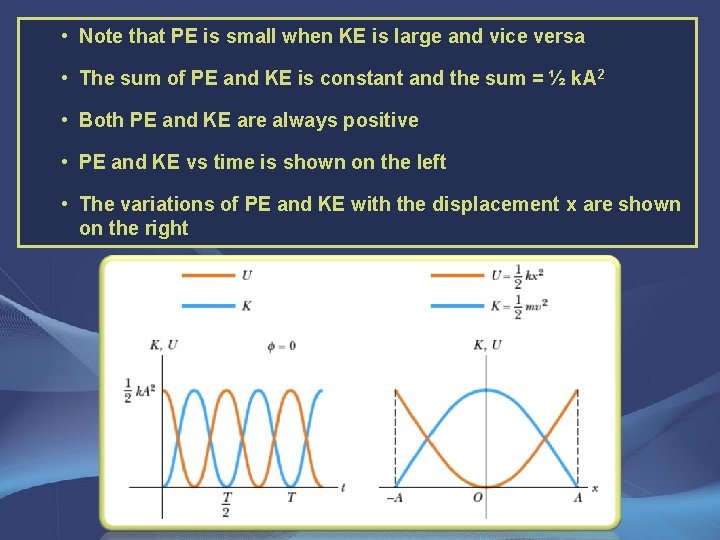
• Note that PE is small when KE is large and vice versa • The sum of PE and KE is constant and the sum = ½ k. A 2 • Both PE and KE are always positive • PE and KE vs time is shown on the left • The variations of PE and KE with the displacement x are shown on the right

Velocity as a function of position for a Simple Harmonic Oscillator

The Simple Pendulum

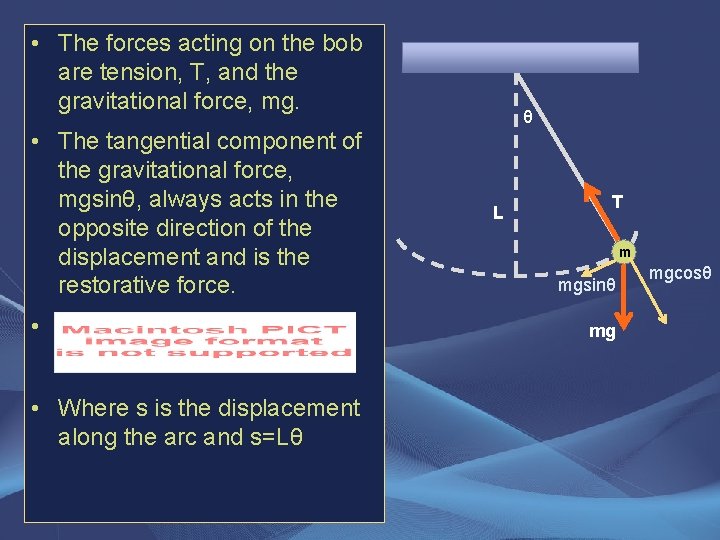
• The forces acting on the bob are tension, T, and the gravitational force, mg. • The tangential component of the gravitational force, mgsinθ, always acts in the opposite direction of the displacement and is the restorative force. • • Where s is the displacement along the arc and s=Lθ θ L T m mgsinθ mg mgcosθ

• The equation then reduces to: • θ • But this is not of the form: L T m mgsinθ mg because the second derivative is proportional to sinθ, not θ mgcosθ

• BUT… we can assume that if θ is small that sinθ=θ (this is called the small angle approximation) • So now the equation becomes: θ L T m mgsinθ mg • And now the expression follows that for simple harmonic motion mgcosθ

SHM: The Pendulum • From this equation θ can be written as: • θ = θmaxcos(ωt+Φ) • Θmax is the maximum angular displacement • ω, the angular frequency, is: • because this follows the function • The Period, T of the motion would be:

Damped Oscillations • In many cases dissipative forces (like friction) act on an object. • The Mechanical Energy diminishes with time and the motion is damped • The retarding force can be expressed as: R = -bv (b is a constant, the damping coefficient) • The restoring force can be expressed as F = -kx

Damped Oscillations • When we do the sum of the forces: • The solution to this equation follows the form:

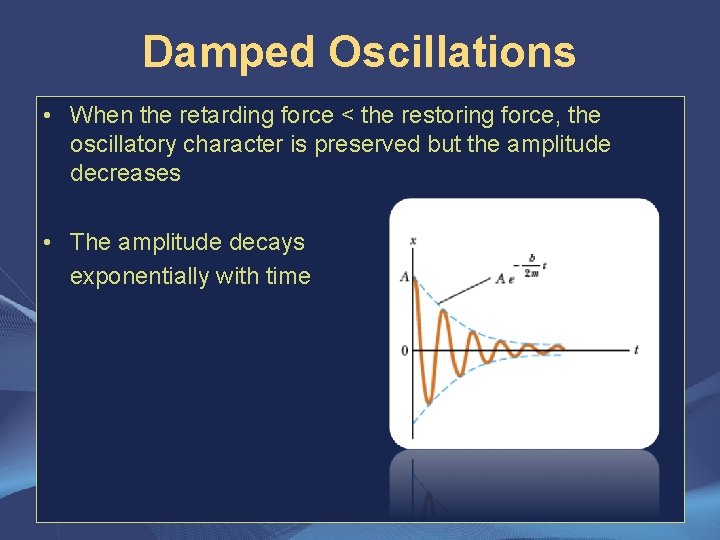
Damped Oscillations • When the retarding force < the restoring force, the oscillatory character is preserved but the amplitude decreases • The amplitude decays exponentially with time

Damped Oscillations • You can also express ω as: • ωo = √(k/m) • ωo is the natural frequency • When the magnitude of the maximum retarding force bvmax< k. A, the system is underdamped • When b reaches a critical value, bc= 2 mωo, the system does not oscillate and is critically damped • If the retarding force is greater than the restoring force, bvmax > k. A, the system is overdamped

Forced Oscillations • The amplitude will remain constant if the energy input per cycle equals the energy lost due to damping • This type of motion is called a force oscillation • Then the sum of the forces becomes:

Forced Oscillations • The solution to this equation follows the form:

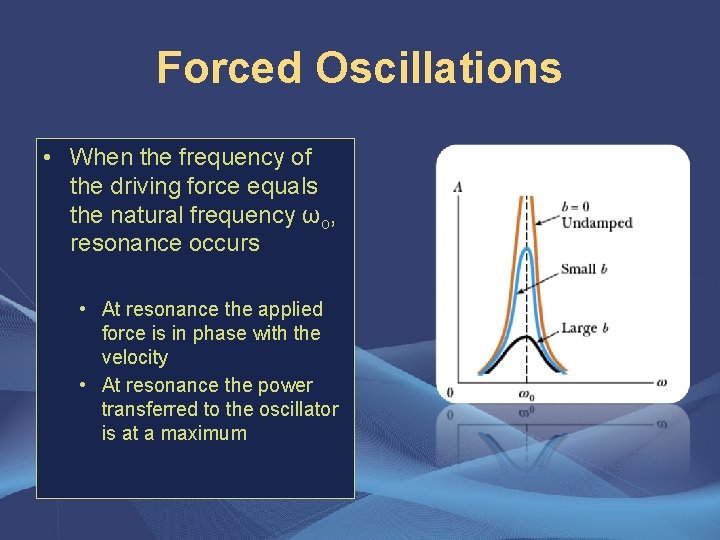
Forced Oscillations • When the frequency of the driving force equals the natural frequency ωo, resonance occurs • At resonance the applied force is in phase with the velocity • At resonance the power transferred to the oscillator is at a maximum
 Energy of harmonic oscillator
Energy of harmonic oscillator Simple harmonic oscillator
Simple harmonic oscillator Harmonic oscillator selection rules
Harmonic oscillator selection rules Migratory aptitude is greater for
Migratory aptitude is greater for Simple harmonic oscillator amplitude
Simple harmonic oscillator amplitude 戴明鳳
戴明鳳 Simple harmonic oscillator
Simple harmonic oscillator Nn.linear
Nn.linear What is shm
What is shm Morse potential
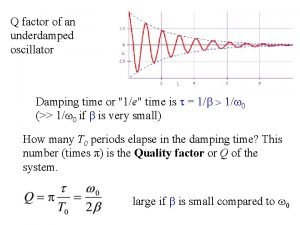
Morse potential Q factor damped harmonic oscillator
Q factor damped harmonic oscillator Relaxation time of damped harmonic oscillator
Relaxation time of damped harmonic oscillator Harmonic oscillator propagator
Harmonic oscillator propagator Harmonic oscillator spring
Harmonic oscillator spring Zero point energy formula
Zero point energy formula Tension wave
Tension wave Simple harmonic motion notes
Simple harmonic motion notes Simple lc oscillator circuit
Simple lc oscillator circuit How to calculate useful energy output
How to calculate useful energy output