END 503 Dorusal Programlama YAPAY DEKEN KULLANIMI Kara

END 503 Doğrusal Programlama YAPAY DEĞİŞKEN KULLANIMI İ. Kara, 2007

Büyük M Yöntemi P: Ax = b x≥ 0 k. a. ENK x 0=Cx P(M): İ. Kara, 2007 Ax+xa = b x, xa ≥ 0 k. a. ENK x 0=Cx+MΣxai

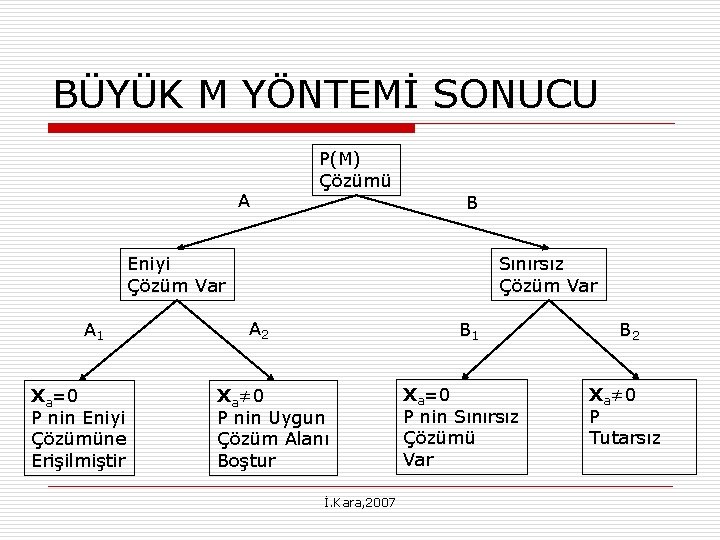
BÜYÜK M YÖNTEMİ SONUCU A P(M) Çözümü B Eniyi Çözüm Var A 1 Xa=0 P nin Eniyi Çözümüne Erişilmiştir Sınırsız Çözüm Var A 2 B 1 Xa≠ 0 P nin Uygun Çözüm Alanı Boştur İ. Kara, 2007 Xa=0 P nin Sınırsız Çözümü Var B 2 Xa≠ 0 P Tutarsız

A 1: P(M)’nin Eniyi Çözümü (X, 0) x 0 = Cx + MΣxai, Enk x 0 Cx ≤ Cx + MΣxai Xai = 0 Cx ≤ Cx P’nin eniyi çözümü İ. Kara, 2007

A 2: P(M)’nin Eniyi Çözümü (x, xa), xa≠ 0 P’nin en az bir uygun çözümü olsun ve x# ile gösterilsin. (x#, 0) P(M) uygun çözümü olur ki, (x, xa) eniyi çözüm olduğundan, Cx + Mxa ≤ C x# yazılır. İ. Kara, 2007

A 2: Devam x, xa ve x# ≥ 0 iken M>0 ve çok büyük olduğundan bu eşitsizlik mümkün değildir. O halde, P’nin bir uygun çözümü olamaz ki, P’nin uygun çözüm alanı boş demektir. İ. Kara, 2007

B 1: P(M) Sınırsız xa=0 P(M) sınırsız Э d=(d 1, d 2) ≥ 0 Cd 1 + Md 2 < 0 M>0 ve çok büyük olduğundan, d 2=0 demektir ki Cd 1<0, d 1 ≥ 0 elde edilir. P sınırsızdır. İ. Kara, 2007

B 2: xa≠ 0, xk temele girebilir, Yk≤ 0 Tüm yapay değişkenler için Σyij ≤ 0 dır. zj-Cj = Σciyij + M(Σyij) – Cj Enb{zj-cj} = zk-ck Simpleks tablosunun yapay değişkenlere karşı gelen ana blok satırları toplanırsa Σxi + Σxj(Σyij) = Σbi bulunur. İ. Kara, 2007

B 2: Devam P’nin en az bir uygun çözümü varsa, xi=0, xj≥ 0 olacağından, Σyij≤ 0 iken, Σbi≥ 0 olamaz. P tutarsız olup, uygun çözüm alanı boş demektir. İ. Kara, 2007

ÖRNEK: Büyük M İ. Kara, 2007

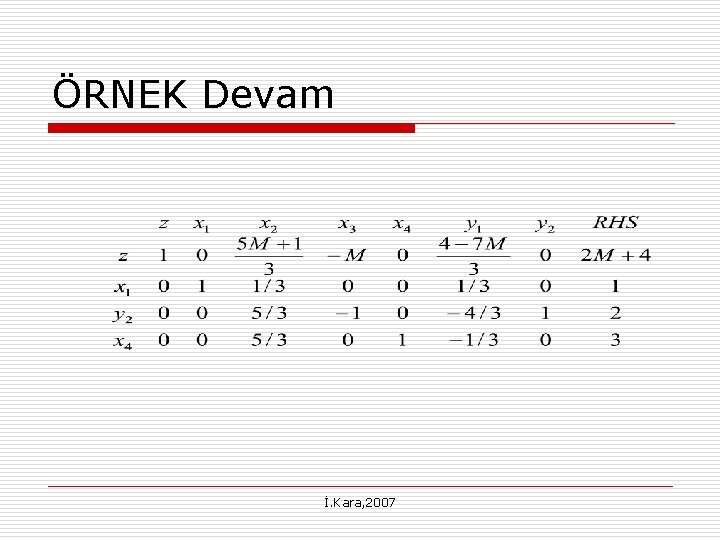
ÖRNEK Devam İ. Kara, 2007

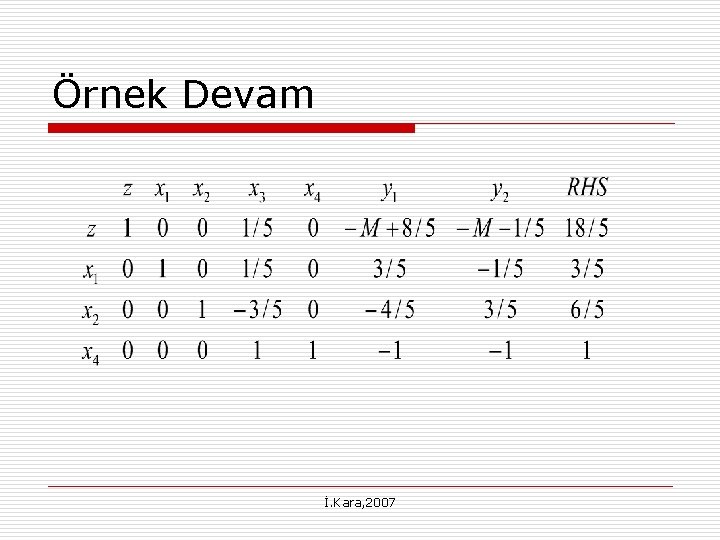
Örnek Devam İ. Kara, 2007

İki Evreli Simpleks Algoritması P: Ax + Y = b x≥ 0 Y≥ 0 k. a. ENK(ENB) Y 0=? İ. Kara, 2007

1. Evre Ax + Y = b x ≥ 0, Y ≥ 0 k. a. ENB Y 0=Σ-yi veya ENK Y 0=Σyi 1. Eniyi y 0 = 0 o o 2. Temelde yi yok. Temelde yi var ama sıfır değerini almış. Eniyi y 0 ≠ 0 UÇA boş. DUR İ. Kara, 2007

2. Evre 1. Tüm yapay değişkenler temel dışı a) b) 2. (x 0 satırı x 0=Cx’e göre) B-1 gerekiyorsa yi lere (0) katkı ver. SA uygula. B-1 gerekmiyorsa, yi lere karşı gelen sütunu çıkart SA uygula. Temelde sıfır değeriyle yapay değişken var o SA’nı yapay değişkenler temele girmeyecek şekilde uygula. İ. Kara, 2007

Temelde sıfır değeriyle yer alan yapay değişkenler var xk temele girecek değişken iken buna karşı gelen sütun yk olsun. xk STS zk-ck x 0 y 1 k y 2 k b 1 b 2 yik 0 ymk bm yi + yik = 0 İ. Kara, 2007

i. ii. yik ≥ 0 tüm yapay değişkenler için enküçük oran testi xk girer, karşı gelen yapay değişken çıkar. xk=0 ve x 0=0 olur. Bazı i’ler için yik<0. xk ↑ yik<0 olduğundan yi ↑ (uygunluk bozulur) xk girer, yi çıkar, xk=0 ve x 0=0 olur. İ. Kara, 2007

Tek Yapay Değişken Tekniği Model Ax=b haline getirildiğinde, A’da I matris var fakat en az bir bi<0 ise başvurulan bir tekniktir. Modelin tüm kısıtlarına, xy≥ 0 bir yapay değişken iken, -xy’yi ekleyelim. İ. Kara, 2007

TEK YAPAY DEĞİŞKEN TEKNİĞİ x 0 XB XR xy 1 0 CBB-1 b-CR 0 I B-1 R İ. Kara, 2007 ST CBB-1 b -1. . . -1 b 1. . . bm

TEK YAPAY DEĞİŞKEN ENK{bi}=br olsun (br<0) br‘a karşı gelen xr temelden çıkartılır, yerine xy temele alınırsa; İ. Kara, 2007

TEK YAPAY DEĞİŞKEN xi + yiyxy = bi x i – x y = bi xr – xy = br, xr=0 xy=-br>0 x i = bi + x y x i = bi – br ≥ 0 i (br<0 ve br≤ 0) A olup, izleyen ardıştırma ile modele bir temle uygun çözüm bulunmuş olur. Bundan sonra, xy bir yapay değişken olarak işlemlere tabi tutulur (Büyük M veya İki Evreli Simpleks Algoritması). İ. Kara, 2007