DORUSAL PRORAMLAMA Yavuz DEMIRDOGEN indekiler Dorusal DP Proramlama

DOĞRUSAL PROĞRAMLAMA Yavuz DEMIRDOGEN

İçindekiler Ø Doğrusal Ø DP Proğramlama (DP) Modeli Ø Grafiksel çözüm Yöntemi Ø Simpleks Çözüm Yöntemi Ø Excel Solver (Çözücü) Ø Tamsayılı Ø Win. QSB Programlama

Doğrusal Programlama Ø Bir Doğrusal Programlama Modeli doğrusal kısıtlar altında bir doğrusal fonksiyonun değerini maksimize yada minimize etmeye çalışır. Ø Doğrusal Programlama belli bir amacı gerçekleştirmek için sınırlı kaynakların etkin kullanımını ve çeşitli seçenekler arasında en uygun dağılımını sağlayan matematiksel bir tekniktir.

Doğrusal Programlama Ø Doğrusal Programlama, optimizasyon problemlerinin çözümünde kullanılan bir yöntemdir. Ø 1947’ de, George Dantzig, doğrusal Programlama problemlerinin çözümünde kullanılan etkin bir yol olan Simpleks Algoritma’ yı buldu ve bu buluşla birlikte doğrusal Programlama, sıklıkla ve hemen her sektörde kullanılmaya başlandı.

Doğrusal Fonksiyonlar �y = mx+b bir doğrunun denklemidir. ör. y = -4/3 x +6 3 y= -4 x+18 yada 4 x + 3 y = 18 �Bir Doğrusal Fonksiyon bir pozitif, negatif veya 0 sabitinin değişkenlerle çarpımlarının toplamıdır; ör. 5 X 1 - 4 X 2 + 0 X 3 + 6 X 4 X 1^2, X 1/X 2, e^-x 2, √X 1, vb. yer almaz

Doğrusal Kısıtlar Doğrusal kısıtlar şu şekle sahiptir <Bir Doğ. Fonksiyon> <Bir İlişki> <Bir Sabit> Örnekler: v 4 X 1 + 5 X 2 - 6 X 3 + 2 X 5 ≤ 34 v 2 X 1 - 5 X 2 + 1 X 4 ≥ 47 v- 2 X 2 + 8 X 3 + 9 X 4 + 2 X 5 = 67 v. X 1 ≥ 0 v X 5 ≥ 0

Doğrusal Programlama (DP) Modeli Ø Max/min Ø Kısıtlar: Ø Ø bm Ø Ø Z = c 1 x 1 + c 2 x 2 +. . . + cnxn a 11 x 1 + a 12 x 2 +. . . + a 1 nxn (≤, =, ≥) b 1 a 21 x 1 + a 22 x 2 +. . . + a 2 nxn (≤, =, ≥) b 2 : am 1 x 1 + am 2 x 2 +. . . + amnxn (≤, =, ≥) xj = Karar değişkenleri bi = Kısıtlama Seviyesi cj = Karar Değişkeni Katsayısı aij = Kısıtlama Katsayıları

DP Modelinin Bileşenleri ü Bir Doğrusal Programlama Modeli şu bileşenlere sahiptir: Ø Bir grup karar değişkeni. (X 1, X 2 gibi) Ø Bir Amaç Fonksiyonu. Zmax/min = c 1 x 1 + c 2 x 2 +. . . cnxn Ø Bir grup kısıtlık. a 11 x 1 + a 12 x 2 +. . . + a 1 nxn (≤, =, ≥) b 1 a 21 x 1 + a 22 x 2 +. . . + a 2 nxn (≤, =, ≥) b 2

DP Modelleri Neden Önemlidir Ø Bir çok Gerçek Hayat Problemi DP ile Modellenebilir. Ø Üretim, Pazarlama, Finans, Reklam, Tarım, Enerji gibi bir çok alanda bildik iyi uygulamalar vardır. Ø Doğrusal Programlama modellerinin çözümü İçin kullanılabilen etkin çözüm teknikleri vardır. Ø Doğrusal Programlama Modellerinin çözümü için geliştirilen yazılımlar çözüm sonrası analizler açısından oldukça güçlüdürler.

DP Modelinin Varsayımları ü Doğrusallık: Modeldeki fonksiyonların hepsi doğrusaldır. ü Kısıtlık: Kaynakların sınırlı olduğunu öngörür. ü Kesinlik: Tüm parametrelerin kesin olarak bilindiğini ve ilgili dönemde değişmeyeceğini öngörür. ü Negatif Olmama: Karar değişkenleri negatif değerler alamazlar. ü Bölünebilirlik : Her karar değişkenlerinin ondalıklı bir sayı alabileceği anlamına gelir.

DP Problemlerinin Modelinin Kurulması üDP Problemlerinin modelinin kurulmasında aşağıdaki adımların izlenmesi gerekmektedir. ØKarar değişkenlerinin tanımlanması ve bunların sembolize edilmesi ØAmacın belirlenerek amaç fonksiyonun karar değişkenlerinin doğrusal bir fonksiyonu olarak yazılması ØTüm kısıtlamaların karar değişkenlerinin doğrusal bir fonksiyonları olarak eşitlik veya eşitsizlik olarak yazılması ØNegatif olmama koşullarının yazılması.

Temel Kavramlar Ø Çözüm: Bir doğrusal programlama probleminin kısıtlayıcı fonksiyonlarının hepsini birden sağlayan karar değişkenlerinin (x 1, x 2, . . . , xn) oluşturduğu kümeye çözüm denir. Ø Uygun çözüm: Negatif olmama koşulunu sağlayan çözüme uygun çözüm denir. Ø En iyi çözüm: Amaç fonksiyonuna en iyi değeri (en küçük veya en büyük) sağlayan uygun çözüme en iyi çözüm denir.

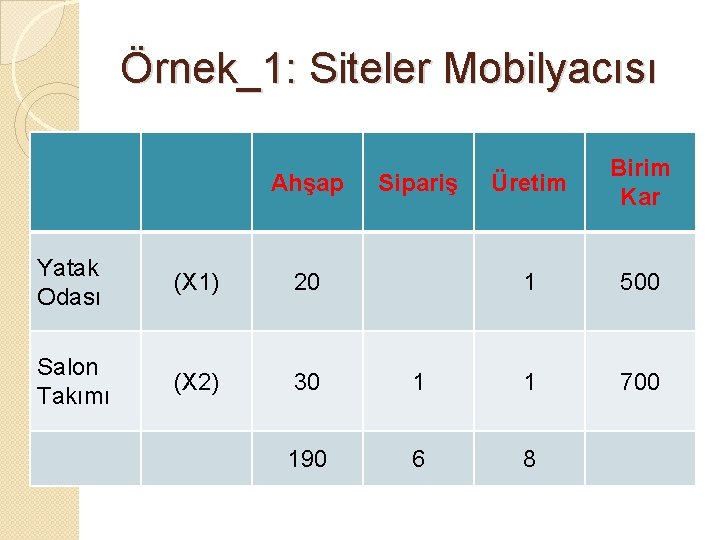
Örnek_1: Siteler Mobilyacısı �Siteler mobilyacısı ahşaptan salon takımı ve yatak odası takımı üretmektedir. Yatak odası takımının karı 500 TL, Salon takımının karı 700 TL dir. Yatak odası takımı aylık en fazla 6 adet sipariş almaktadır. Marangoz aylık 8 adet takım üretebilmektedir. Toplam ahşap miktarı 190 m 2, bir salon takımı 30 m 2 ahşaptan, bir yatak odası takımı 20 m 2 ahşaptan yapılmaktadır. Siteler mobilyacısı maksimum kar elde edebilmek için takımlardan kaçar adet üretmelidir?

Örnek_1: Siteler Mobilyacısı Ahşap Sipariş Üretim Birim Kar 1 500 700 Yatak Odası (X 1) 20 Salon Takımı (X 2) 30 1 1 190 6 8

Örnek_1: Siteler Mobilyacısı ü KARAR DEĞİŞKENLERİ vÜretilecek Salon ve Yatak Odası Takımları ØYatak Odası Takımı : X 1 ØSalon Takımı : X 2 ü AMAÇ FONKSİYONU v“En Yüksek Karı Elde Etmek” (Takımlardan Elde Edilecek Kar Toplamını Maksimize Etmek”) ØYatak Odası Takımından Elde Edilecek Kar; ØYatak Odası Takımı Sayısı * Birim Kar = X 1*500 ØSalon Takımından Elde Edilecek Kar; ØSalon Takımı sayısı * Birim Kar = X 2*700 ØToplam Kar = Salon Odası Takımı Karı + Yatak Odası Takımı Karı Ø= 500 X 1 + 700 X 2

Örnek_1: Siteler Mobilyacısı ü Kısıtlar Ø Yatak Odası Takımı Sipariş Kısıtı Ø X 1 <= 6 Ø Ahşap Kısıtı Ø 20 X 1 + 30 X 2 <= 190 Ø Üretim Kısıtı Ø X 1 + X 2 <= 8 Ø Negatif Olmama Kısıtı Ø X 1 >= 0 ve X 2 >= 0

Örnek_1: Model Ø Max: Zmax = 500 X 1 + 700 X 2 Ø Kısıtlar: 20 X 1 + 30 X 2 <= 190 X 1 <= 6 X 1 + X 2 <= 8 X 1 >= 0 ve X 2 >= 0 (Ahşap Kısıtı) (Sipariş Kısıtı) (Üretim Kısıtı)

Grafiksel Çözüm Yöntemi Ø Bir doğrusal programlama probleminin grafik çözümünde aşağıdaki adımlar izlenir: v Değişkenlerin koordinat sisteminin yatay ve dikey eksenlerine yerleştirilmesi, v Kısıtlayıcı fonksiyonların grafiğinin çizilmesi, v Uygun çözüm bölgesinin belirlenmesi, v En iyi çözümün araştırılması.

Örnek_1: Grafiksel Çözüm 1. AŞAMA : Negatif Olmama Kısıtlarının Sağlanması X 2 X 1

Örnek_1: Grafiksel Çözüm 2. AŞAMA: Sipariş Kısıtının Sağlanması

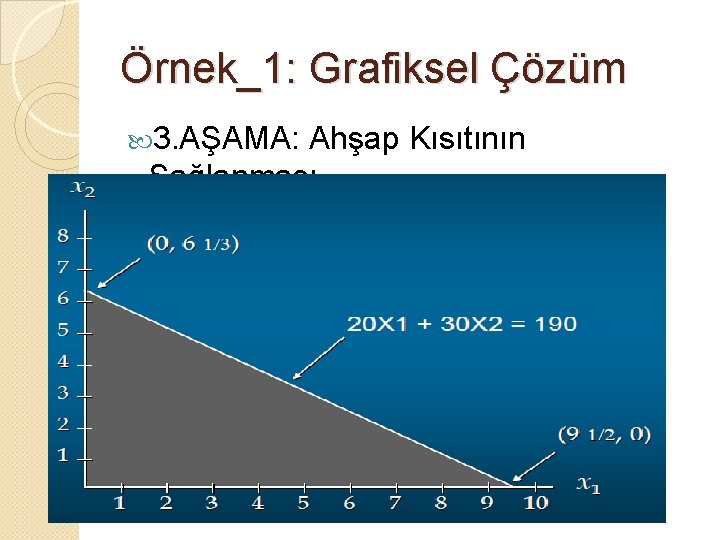
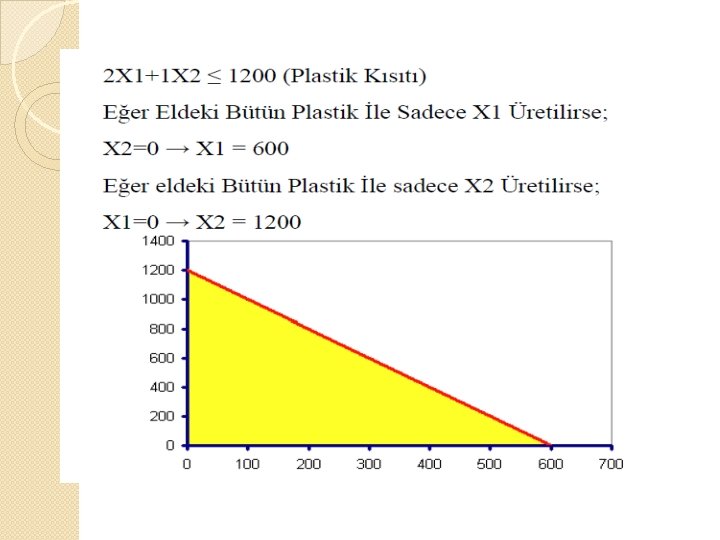
Örnek_1: Grafiksel Çözüm 3. AŞAMA: Ahşap Kısıtının Sağlanması Ahşap Kısıtı: 20 X 1 + 30 X 2 = 190 Sadece Yatak Odası Takımı Üretilirse X 2 = 0 20 X 1 = 190 => X 1 = 190/20 = 9, 5 Sadece Salon Takımı Üretilirse X 1 = 0 30 X 2 = 190 => X 2 = 190/30 = 6, 33

Örnek_1: Grafiksel Çözüm 3. AŞAMA: Ahşap Kısıtının Sağlanması

Örnek_1: Grafiksel Çözüm 4. AŞAMA: Üretim Kısıtının Sağlanması Üretim Kısıtı: X 1 + X 2 = 8 Sadece Yatak Odası Takımı Üretilirse X 2 = 0 X 1 = 8 Sadece Salon Takımı Üretilirse X 1 = 0 X 2 = 8

Örnek_1: Grafiksel Çözüm 3. AŞAMA: Üretim Kısıtının Sağlanması

Örnek_1: Grafiksel Çözüm 4. AŞAMA: Kısıtların Grafiksel birleşimi

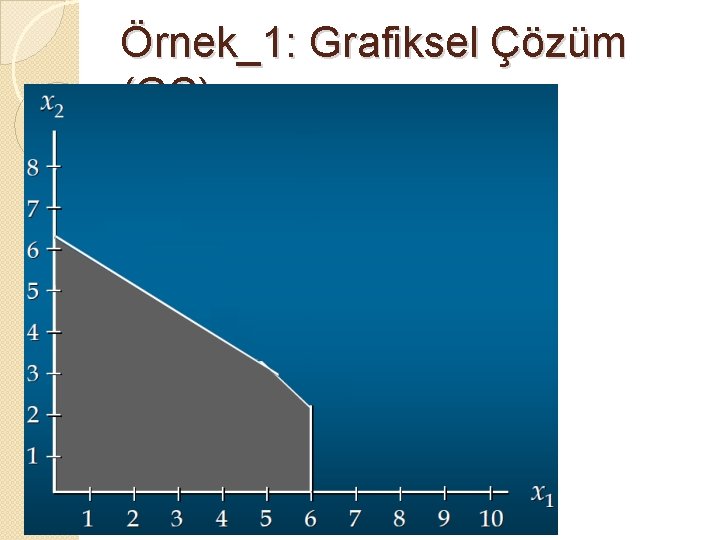
Örnek_1: Grafiksel Çözüm

Örnek_1: Grafiksel Çözüm (GÇ) �A ve D noktalarının koordinatlarını biliyoruz. �B ve C noktalarının koordinatlarını hesaplayalım. �B noktası X 1+X 2=8 ve 20 X 1+30 X 2=190 doğrularının kesişim noktası olduğundan ◦ X 1+X 2=8 ◦ 20 X 1+30 X 2=190 => X 1=3 ve X 2=5 olur. �C noktası X 1+X 2=8 ve X 2= 6 doğrularının kesişim noktası olduğundan ◦ X 1+X 2=8 ◦ X 1 = 6 => X 2=2 olur.

Örnek_1: Grafiksel Çözüm (GÇ)

Örnek_1: Grafiksel Çözüm (GÇ) Kısıtlılıklara göre belirlenen taralı bölgenin uç noktalarından biri optimal çözüm noktasıdır. Bu noktayı iki yöntemle belirleyebiliriz. ◦ Deneme Yanılma Yöntemi ◦ Kayıtsızlık Eğrileri Yöntemi

Örnek_1: Grafiksel Çözüm (GÇ) Deneme-Yanılma Yaklaşımı ◦ Her noktadaki üretim miktarını hesapla ◦ Amaca olan katkıyı hesapla ◦ Amaca en fazla katkı sağlayan nokta optimum noktadır.

Örnek_1: GÇ Deneme. Yanılma Uç noktaların amaç fonksiyonuna katkıları belirlenmeli ◦ A noktası için: X 1=0 ve X 2=6. 33 Zmax=500 X 1+700 X 2 => Zmax= 4431 TL ◦ B noktası için: X 1=5 ve X 2= 3 Zmax=500 X 1+700 X 2 => Zmax= 4600 TL ◦ C noktası için: X 1=6 ve X 2= 2 Zmax=500 X 1+700 X 2 => Zmax= 4400 TL ◦ D noktası için: X 1=6 ve X 2= 0 Zmax=500 X 1+700 X 2 => Zmax= 3000 TL

Örnek_1: GÇ Deneme. Yanılma Görüldüğü gibi B noktasındaki 4600 liralık kar en büyük olduğu için optimal çözüm noktası B noktasıdır. Siteler mobilyacısı mevcut kısıtlılıklar içinde, en fazla kar elde edebilmek için 5 yatak odası takımı ve 3 salon takımı üretmelidir. Zmax=500 X 1+700 X 2 => Zmax= 4600 TL ◦ X 1 = 5 (Yatak Odası Takımı) ◦ X 2 = 3 (Salon Takımı) ◦

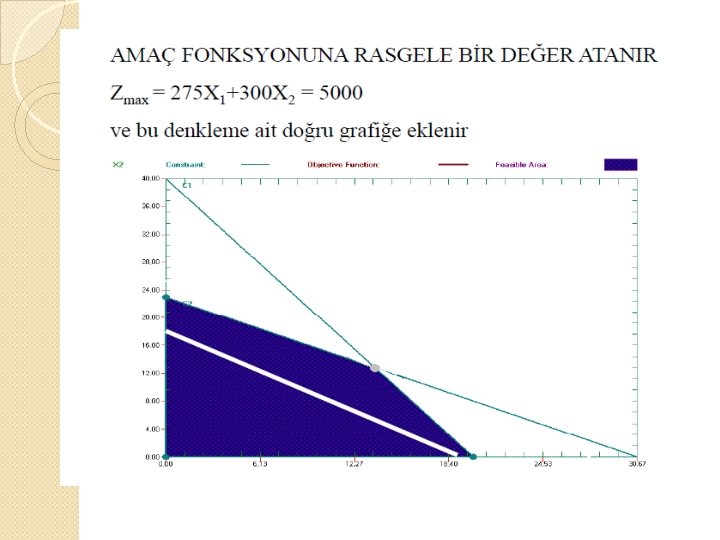
Örnek_1: Grafiksel Çözüm (GÇ) Ø Kayıtsızlık Eğrileri Yaklaşımı ◦ Amaç fonksiyonuna rastgele bir değer verilir ◦ Amaç doğrusu belirlenir ve çizilir ◦ Amaç doğrusu çözüm alanı içinde kaydırılarak optimum çözüm noktası bulunur.

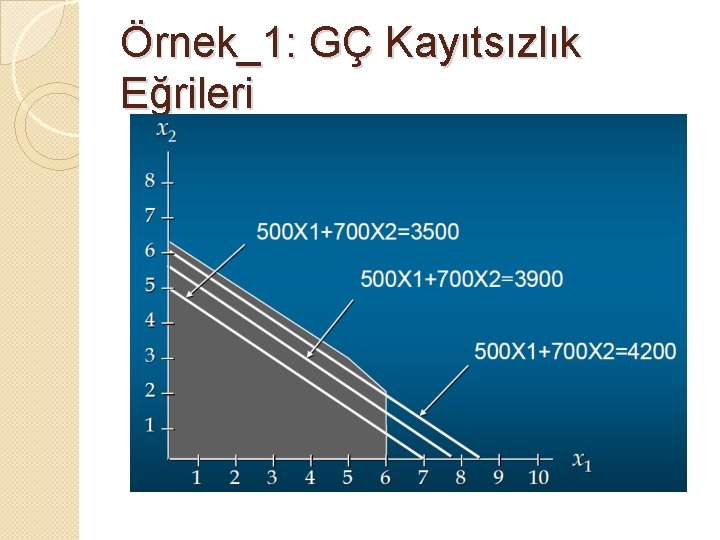
Örnek_1: GÇ Kayıtsızlık Eğrileri 1. Amaç fonksiyonuna bir değer verelim. ◦ ◦ ◦ Zmax=500 X 1+700 X 2 Zmax= 3500 olsun. X 1=0 için X 2=3500/700 => X 2 = 5 olur. X 2=0 için X 1=3500/500 => X 1 = 7 olur. 2. Amaç doğrusunu çizelim 3. Amaç doğrusunu kaydıralım

Örnek_1: GÇ Kayıtsızlık Eğrileri

Örnek_1: GÇ Kayıtsızlık Eğrileri

Örnek_1: GÇ Kayıtsızlık Eğrileri

Örnek_2: Minimizasyon problemi Ankara Boyacısı Siyah ve Renkli boya üretmektedir. Her ay en az 30 ton Siyah ve 20 ton renkli boya üretmesi gerekmektedir. Aylık en az 60 ton boya üretilmelidir. Siyah boyanın aylık üretim maliyeti 2500 TL ve Renkli boyanın aylık maliyeti ise 3000 TL dir. Üretim maliyetini minimize etmek için boyalardan ne kadar üretilmelidir?

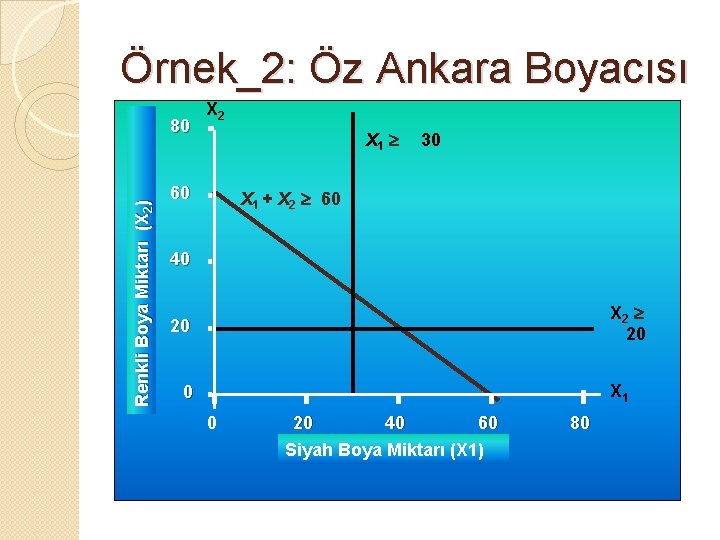
Örnek_2: Öz Ankara Boyacısı Karar Değişkenleri Amaç fonksiyonu ◦ X 1 = Üretilecek Siyah Boya miktarı ◦ X 2 = Üretilecek Renkli Boya miktarı ◦ Minimizasyon Zmin = 2500 X 1 + 3000 X 2 Kısıtlar ◦ X 1 30 (Siyah Boya Kısıtı) ◦ X 2 20 (Renkli Boya Kısıtı) ◦ X 1 + X 2 60 (Toplam Aylık Üretim Kısıtı) ◦ X 1 0; X 2 0 (Negatif Olmama Kısıtı)

Örnek_2: Öz Ankara Boyacısı Renkli Boya Miktarı (X 2) 80 X 2 X 1 30 60 X 1 + X 2 60 40 X 2 20 20 X 1 0 0 20 40 60 Siyah Boya Miktarı (X 1) 80

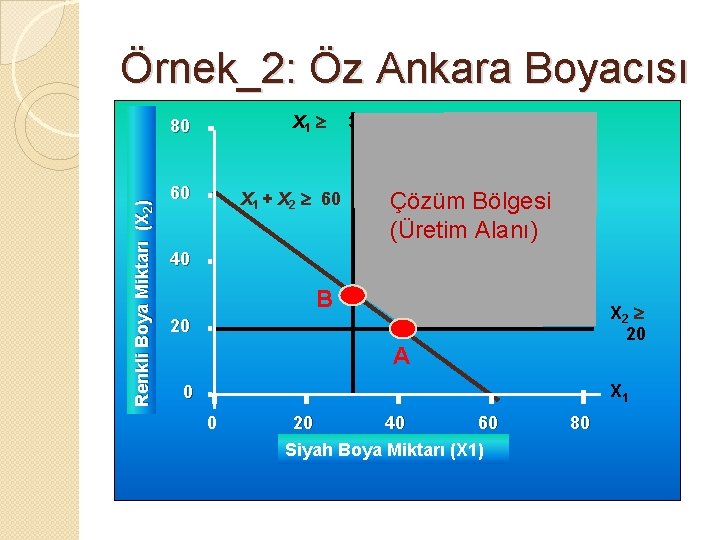
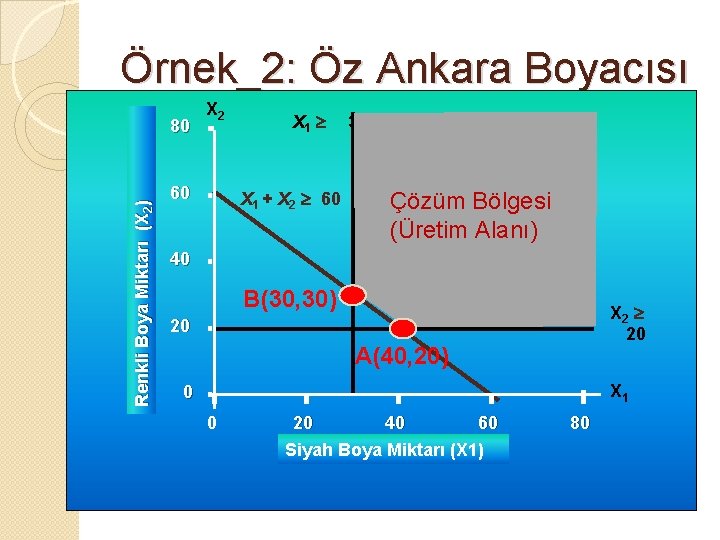
Örnek_2: Öz Ankara Boyacısı X 1 30 Renkli Boya Miktarı (X 2) 80 60 X 1 + X 2 60 Çözüm Bölgesi (Üretim Alanı) 40 B X 2 20 20 A X 1 0 0 20 40 60 Siyah Boya Miktarı (X 1) 80

Örnek_2: Deneme-Yanılma Uç noktaların amaç fonksiyonuna katkıları belirlenmeli ◦ A noktası X 1 + X 2 60 ve X 2 20 doğrularının kesişim noktası olduğundan X 2 = 20 => X 1 + X 2 = 60 => X 1 = 60 - 20 => X 1 = 40 olur. ◦ B noktası X 1 + X 2 60 ve X 1 30 doğrularının kesişim noktası olduğundan X 1 = 30 => X 1 + X 2 = 60 => X 1 = 60 - 30 => X 2 = 30 olur.

Örnek_2: Öz Ankara Boyacısı Renkli Boya Miktarı (X 2) 80 X 2 60 X 1 30 X 1 + X 2 60 Çözüm Bölgesi (Üretim Alanı) 40 B(30, 30) X 2 20 20 A(40, 20) X 1 0 0 20 40 60 Siyah Boya Miktarı (X 1) 80

Örnek_2: GÇ Deneme. Yanılma Uç noktaların amaç fonksiyonuna katkıları belirlenmeli ◦ A noktası için: X 1 = 40 ve X 2 = 20 Zmin = 2500 X 1 + 3000 X 2 => Zmin = 160. 000 TL ◦ B noktası için: X 1 = 30 ve X 2 = 30 Zmin = 2500 X 1 + 3000 X 2 => Zmin = 165. 000 TL

Örnek_2: GÇ Deneme. Yanılma Uç noktaların amaç fonksiyonuna katkıları belirlendiğinde A noktasındaki üretim maliyeti mevcut kısıtlar çerçevesinde en düşük olduğundan optimum çözüm noktası A noktasıdır. ◦ X 1 = 40 ton Siyah Boya üretilmeli ◦ X 2 = 20 ton Renkli Boya üretilmeli ◦ 2500 X 1 + 3000 X 2 = 160. 000 TL (maliyet)

Grafik Çözümde Karşılan Özel Durumlar Eşitsizliklerin Tutarsız Olması Sınırsız Çözüm Uygun Çözüm Bölgesinin Bir nokta Olması Alternatif En iyi Çözümün Bulunması

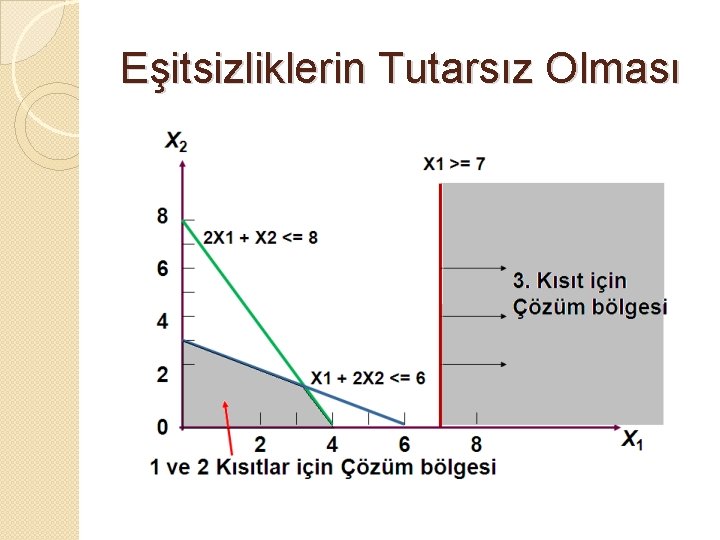
Eşitsizliklerin Tutarsız Olması Mevcut kısıtların tutarsız olması durumudur. Ör: Amaç fonksiyonu: Zmax = X 1 + 2 X 2 olan ve Kısıtlar: X 1 + X 2 <= 20 2 X 1 + X 2 <= 30 X 1 <= 25 X 1, X 2 >= 0 Olarak verilen problemi grafiksel olarak çözersek.

Eşitsizliklerin Tutarsız Olması

Sınırsız Çözüm Sınırsız bir çözüm kümesine sahip olan doğrusal proğramlama; Ör: Zmax = 3 X 1 + 5 X 2 Kısıtlar: X 1 >= 5 X 2 <= 10 X 1 + 2 X 2 >= 10 X 1, X 2 >= 0

Sınırsız Çözüm 15 X 1 > 5 10 Çözüm Bölgesi 5 0 X 2 < 10 X 1 + 2 X 2 > 10 5 10 15

Uygun Çözüm Bölgesinin Bir Nokta Olması Aşağıdaki doğrusal programlama problemini grafik yöntemiyle çözelim. Zmax = 6 x 1 + 3 x 2 x 1 + x 2 £ 6 3 x 1 + 5 x 2 24 x 2 = 3 x 1, x 2 0

Uygun Çözüm Bölgesinin Bir Nokta Olması

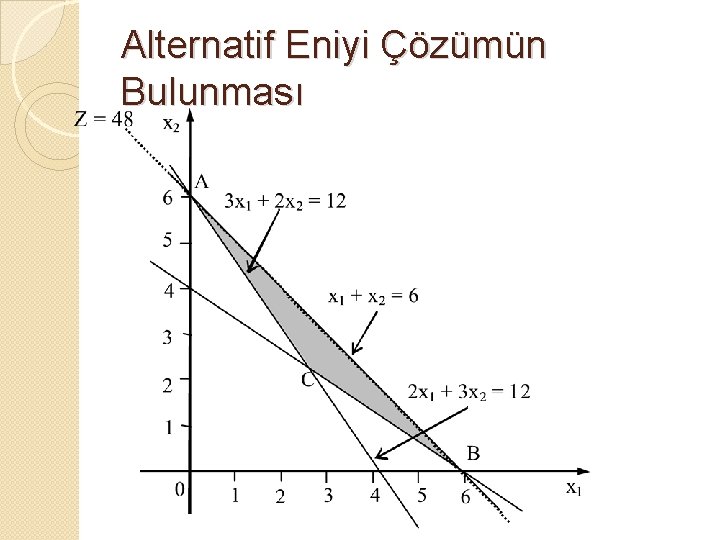
Alternatif Eniyi Çözümün Bulunması Aşağıdaki doğrusal programlama problemini grafik yöntemiyle çözelim. Zmax = 8 x 1 + 8 x 2 2 x 1 + 3 x 2 12 3 x 1 + 2 x 2 12 x 1 + x 2 6 x 1, x 2 0

Alternatif Eniyi Çözümün Bulunması

Alternatif Eniyi Çözümün Bulunması �Uç noktaların amaç fonksiyonuna katkılarını deneme yanılma yöntemiyle belirleyelim. ◦ A noktası için: X 1 = 0 ve X 2 = 6 �Zmax = 8 x 1 + 8 x 2 ise Zmax = 48 ◦ B noktası için: X 1 = 6 ve X 2 = 0 �Zmax = 8 x 1 + 8 x 2 ise Zmax = 48 ◦ C noktası için: � 2 X 1 + 3 X 2 12 ve 3 X 1 + 2 X 2 12 doğrularının kesim noktası X 1 = 2. 4 ve X 2 = 2. 4 �Zmax = 8 x 1 + 8 x 2 ise Zmax = 38. 4 Ø Görüldüğü gibi A ve B noktaları en iyi çözüm

Örnek DP Modeli-1 İnci kimya firması X ve Y gibi iki tip kimyasal madde üretmektedir. 1 litre X ürününün maliyeti 160 TL. , 1 litre Y ürününün maliyeti ise 240 TL. dir. Müşteri talebine göre, firma, gelecek hafta için en az 6 litre X ve en az 2 litre Y ürünü üretmelidir. X ve Y kimyasal ürünlerinde kullanılan hammaddelerden birisinin sunumu azdır ve sadece 30 gr. sağlanabilmektedir. X ürününün bir litresinde bu hammaddeden 3 gr. ve Y nin litresinde de 5 gr. gerekli olmaktadır. İnci firması, toplam maliyetini minimize etmek için X ve Y ürünlerinden kaçar litre üretmesi gerektiği konusunda çok büyük bir kararsızlık içerisine girmiştir. Bu soruyu yanıtlayacak modeli kurunuz.

Örnek DP Modeli-1 Problemde karar değişkenleri, x 1 = Üretilecek X ürününün miktarı ( litre ) x 2 = Üretilecek Y ürününün miktarı ( litre ) Minimize edilmek istenen toplam maliyet 160 x 1 + 240 x 2 dir. İstenen gerekli minimum miktar ise x 1 6 ve x 2 2 dir. Hammadde kısıtlayıcısı ise 3 x 1 + 5 x 2 30 dur. Böylece minimizasyon modeli şöyle olacaktır: Min z = 160 x 1+240 x 2 x 1 6 x 2 2 3 x 1+5 x 2 30 x 1, x 2 0

Örnek DP Modeli-2 Mügesüt şirketi kapasite sorunu yüzünden günde 120. 000 kg. dan daha çok süt işleyememektedir. Yönetim, yağ veya işlenmiş süt için kullanılan sütün dengelenmesi için peynir fabrikasında en az 10. 000 kg. lık günlük süt kullanmak istemektedir. Bir kg. sütün yağ üretimi için kullanıldığında, kara katkısı, 4 TL. , şişe sütü olarak kullanıldığında katkısı 8 TL. ve peynir üretimi için kullanıldığında ise katkısı 6 TL. dir. Yağ bölümü günde 60. 000 kg. , süt şişeleme donanımı günde 40. 000 kg. , peynir donanımı ise günde 30. 000 kg. süt işleyebilir. Şirket karını maksimize etmek istediğine göre problemi doğrusal programlama modeli olarak ifade ediniz.

Örnek DP Modeli-2 Çözüm: Karar Değişkenleri x 1 = Yağ yapımında kullanılan süt miktarı ( kg ) x 2 = Şişelemede kullanılan süt miktarı ( kg ) x 3 = Peynir yapımında kullanılan süt miktarı ( kg ) İşletmenin karını maksimize edecek amaç fonksiyonu; Maksimum z = 4 x 1 + 8 x 2 + 6 x 3 Kısıtlar ise; x 3 10. 000 x 1 60. 000 x 2 40. 000 x 3 30. 000 x 1 + x 2 + x 3 120. 000 Negatif Olmama koşulu; x 1, x 2, x 3 0

Örnek DP Modeli-3 Giapetto tahtadan oyuncak asker ve tren yapmaktadır. Satış fiyatları, bir oyuncak asker için $27, bir oyuncak tren için $21'dır. Bir asker için $10'lık hammadde ve $14'lık işçilik kullanılmaktadır. Bir tren için ise söz konusu rakamlar sırasıyla $9 ve $10'dır. Her bir asker için 2 saat montaj ve 1 saat marangozluk gerekirken, her bir tren için 1 saat montaj ve 1 saat marangozluk gerekmektedir. Eldeki hammadde miktarı sınırsızdır, fakat haftada en çok 100 saat montaj ve 80 saat marangozluk kullanabilen Giapetto'nun haftada en fazla 40 oyuncak asker satabileceğini göz önünde bulundurarak karını enbüyüklemek için hangi oyuncaktan haftada kaç adet üretmesi gerektiğini bulunuz?

Örnek DP Modeli-3 Karar Değişkenleri x 1 = bir haftada üretilen asker sayısı x 2 = bir haftada üretilen tren sayısı İşletmenin karını maksimize edecek amaç fonksiyonu; Maximum z = 3 x 1 + 2 x 2 Kısıtlar ise; s. t. 2 x 1 + x 2 ≤ 100 (Montaj kısıdı) x 1 + x 2 ≤ 80 (Marangozluk kısıdı) x 1 ≤ 40 (Talep kısıdı) Negatif Olmama koşulu; x 1, x 2 ≥ 0

Örnek DP Modeli-3 Grafiksel Çözüm Aşağıdaki kısıtları sağlayan noktalar kümesi olurlu bölgedir. DP’yi sağlayan noktalar kümesi DGFEH beşgeni ile sınırlandırılmıştır. Bu beşgen (boyalı bölge) üzerindeki veya içindeki herhangi bir nokta olurlu bölgededir.

Örnek DP Modeli-3 Eğer (x 1, x 2)’nin bir değeri (bir çözüm) tüm bu kısıtları ve işaret sınırlamalarını sağlarsa, söz konusu çözüm olurlu bölgededir (feasible region). Grafik olarak ya da hesaplayarak sorun çözüldüğünde olurlu bölgedeki çözümlerden amaç fonksiyon değeri en yüksek olan çözümün (x 1, x 2) = (20, 60) olduğunu ve z=180 değerini verdiğini buluruz. Bu çözüm en iyi çözümdür (optimal solution). Rapor Haftada 20 asker ve 60 tren üretilmesi durumunda kar $180 olacaktır. Kar miktarları, eldeki işçilik ve talebe göre elde edilebilecek en büyük kar budur. Daha fazla işçilik bulunursa kar çoğalabilir.

Örnek DP Modeli-4 Dorian şirketi, yüksek gelirli müşterileri için otomobil ve jeep üretmektedir. Televizyondaki tiyatro oyunlarına ve futbol maçlarına bir dakikalık spot reklamlar vererek satışlarını arttırmayı hedeflemektedir. Tiyatro oyununa verilen reklamın maliyeti $50 bin'dir ve hedef kitledeki 7 milyon kadın ve 2 milyon erkek tarafından seyredilebilir. Futbol maçına verilen reklamın maliyeti ise $100 bin'dir ve hedef kitledeki 2 milyon kadın ve 12 milyon erkek tarafından seyredilebilir. Dorian yüksek gelirli 28 milyon kadın ve 24 milyon erkeğe en az maliyetle nasıl ulaşır?

Örnek DP Modeli-4 Karar değişkenleri aşağıdaki gibi belirlenebilir: x 1 = tiyatro oyununa verilen reklam sayısı x 2 = futbol maçına verilen reklam sayısı Sorunun modeli: min z = 50 x 1 + 100 x 2 öyle ki 7 x 1 + 2 x 2 ≥ 28 2 x 1 + 12 x 2 ≥ 24 x 1, x 2≥ 0

Örnek DP Modeli-4 Grafiksel Çözüm Dorian toplam reklam maliyetini enküçüklemek istediği için sorunun en iyi çözümü olurlu bölgede en az z değerini veren noktadır. En az z değerli eş maliyet doğrusu E noktasından geçmektedir; bu yüzden en iyi çözüm x 1 = 3. 6, x 2 = 1. 4 ve z = 320 şeklindedir. Hem yüksek gelirli kadın hem de yüksek gelirli erkek kısıtları sağlandığı için her ikisi de aktif kısıtlardır.

Örnek DP Modeli-4 Grafik çözüm yapılırsa (x 1, x 2) = (3. 6, 1. 4) değerleri için amaç fonksiyonunun en iyi değeri z = 320 olarak bulunur. Grafiğe bakılarak en iyi tamsayılı çözüm (x 1, x 2) = (4, 2) olarak bulunabilir. Rapor Hedeflenen kitleye ulaşmak için en az maliyetli çözüm 4 adet reklamı tiyatro oyununda ve 2 adet reklamı futbol maçında kullanmak gerekir. Bu durumda Dorian $400 bin reklam masrafı yapacaktır.

Örnek DP Modeli-5 Two Mines Şirketi özel bir cevher çıkardığı iki adet maden ocağına sahiptir. Ocaklarda üretilen cevher üç sınıfa ayrılır: yüksek, orta, düşük kaliteli. Şirket bir fabrikaya haftalık olarak 12 ton yüksek, 8 ton orta ve 24 ton düşük kaliteli cevher sağlamak üzere anlaşmıştır. Söz konusu iki maden ocağı (X ve Y) ayrıntıları aşağıda verilen farklı işletim özelliklerine sahiptir. Anlaşmayı gerçekleştirmek için haftasonu üretim yapılmayan maden ocakları haftada kaç gün işletilmelidir? Maden Maliyet Üretim (ton/gün) (£'000 / gün) Yüksek Orta Düşük X 180 6 3 4 Y 160 1 1 6

Örnek DP Modeli-5 Sorunun Modeli enküçükle (minimize) 180 x + 160 y öyle ki (subject to) 6 x + y >= 12 3 x + y >= 8 4 x + 6 y >= 24 x <= 5 y <= 5 x, y >= 0

Örnek DP Modeli-5 Grafik Çözümü En iyi çözüm için maliyet 765. 71’dir. 1. 71 gün X madeni ve 2. 86 gün Y madeni çalıştırılmalıdır.

Örnek DP Modeli-6 Bayan Fidan dört "temel gıda grubu" ile beslenmektedir: kek, çikolatalı dondurma, kola, ananaslı pasta. Bir adet kek $0. 5'a, bir kaşık dondurma $0. 2'a, bir şişe kola $0. 3'a ve bir dilim pasta $0. 8'a satılmaktadır. Her gün en az 500 kalori, 6 oz. çikolata, 10 oz. şeker ve 8 oz. yağ alması gereken Bayan Fidan en az maliyetle bu gereksinimlerini nasıl karşılar? Aşağıdaki tabloyu kullanarak bir DP modeli kurup sorunu çözünüz. Kalori Çikolata Şeker Yağ (ounce) e) Kek (1 adet) 400 3 2 2 Çikolatalı dondurma (1 kaşık) 200 2 2 4 Kola (1 şişe) 150 0 4 1 Ananaslı pasta (1 dilim) 500 0 4 5

Örnek DP Modeli-6 Karar değişkenleri: x 1: günlük yenilecek kek sayısı x 2: günlük yenilecek kaşık dondurma sayısı x 3: günlük içilecek şişe kola sayısı x 4: günlük yenilecek dilim pasta sayısı şeklinde belirlenebilir. Bu durumda amaç fonksiyonu (cent cinsinden toplam günlük maliyet): min w = 50 x 1 + 20 x 2 + 30 x 3 + 80 x 4 Kısıtlar: 400 x 1 + 200 x 2 + 150 x 3 + 500 x 4 > 500 (günlük kalori) 3 x 1 + 2 x 2 > 6 (günlük çikolata)

Örnek DP Modeli-6 Rapor Bayan Fidan günde 3 kaşık dondurma yiyip 1 şişe kola içerek tüm besin gereksinimlerini karşılayabilir ve sadece 90 cent harcar (w=90, x 2=3, x 3=1).

Örnek DP Modeli-7 Bir postanede haftanın her günü farklı sayıda elemana gereksinim duymaktadır. Sendika kurallarına göre bir eleman 5 gün peşe çalışmakta diğer iki gün izin yapmaktadır. Çalıştırılması gereken toplam en az eleman sayısını aşağıdaki iş yüküne göre hesaplayınız. Pzt Sal Çar Per Cum Cmt Paz Gerekli eleman 17 13 15 19 14 16 11

Örnek DP Modeli-7 Karar değişkenleri xi (i. gün çalışmaya başlayan eleman sayısı) olsun Matematiksel olarak DP modeli aşağıdaki gibi oluşturulabilir: min z = x 1 +x 2 +x 3 +x 4 +x 5 +x 6 +x 7 x 1 +x 4 +x 5 +x 6 +x 7 ≥ 17 x 1 +x 2 +x 5 +x 6 +x 7 ≥ 13 x 1 +x 2 +x 3 +x 6 +x 7 ≥ 15 x 1 +x 2 +x 3 +x 4 +x 7 ≥ 19 x 1 +x 2 +x 3 +x 4 +x 5 ≥ 14 +x 2 +x 3 +x 4 +x 5 +x 6 ≥ 16 +x 3 +x 4 +x 5 +x 6 +x 7 ≥ 11 xt≥ 0,

Örnek DP Modeli-7 Rapor (xt) = (4/3, 10/3, 2, 22/3, 0, 10/3, 5), z = 67/3 şeklindedir. Karar değişkeni değerleri yakın tamsayılara yuvarlanırsa (xt) = (2, 4, 2, 8, 0, 4, 5), z=25 çözümü bulunur (yanlış olabilir!). Elde edilen Tamsayılı Lindo çözümüne göre ise amaç fonksiyonun en iyi değeri z=23'dür ve (xt) = (4, 4, 2, 6, 0, 4, 3) şeklindedir.

Örnek DP Modeli-8 Sailco şirketi gelecek dört mevsimde kaç adet yelkenli üreteceğine karar verecektir. Talep sırasıyla 40, 60, 75 ve 25 yelkenlidir. Sailco tüm talepleri zamanında karşılamalıdır. Başlangıçta Sailco'nun envanterinde 10 yelkenli vardır. Normal mesai ile bir mevsimde 40 yelkenli üretebilen şirket yelkenli başına $400 işçilik maliyetine maruz kalmaktadır. Fazla mesai ile yapılan her ek yelkenli için ise işçilik maliyeti $450'dır. Herhangi bir mevsimde yapılan yelkenli ya talebi karşılamak için kullanılıp satılır ya da envantere konulur. Bir yelkenlinin bir mevsim envanterde tutulması durumunda ise $20 envanter taşıma maliyeti oluşmaktadır.

Örnek DP Modeli-8 t = 1, 2, 3, 4 için karar değişkenleri xt = t. mevsimde normal mesai ile üretilen yelkenli sayısı yt = t. mevsimde fazla mesai ile üretilen yelkenli sayısı Envanter hesaplarının yapılabilmesi için kullanılacak değişkenler: it = t. mevsimin sonunda envanterdeki yelkenli sayısı dt = t. dönem için yelkenli talebi Veri xt ≤ 40, ∀t Mantıksal olarak it = it-1+ xt + yt - dt, ∀t. Talep karşılanmalı it ≥ 0, ∀t (İşaret sınırlamaları xt, yt≥ 0, ∀t) Bu kısıt kümelerini kullanarak toplam maliyet z’yi enküçüklemeliyiz: z = 400(x 1+x 2+x 3+x 4) + 450(y 1+y 2+y 3+y 4) + 20(i 1+i 2+i 3+i 4)

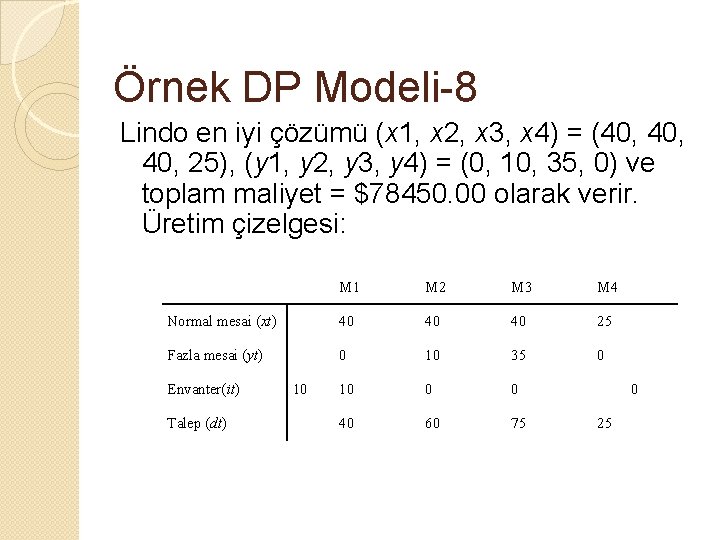
Örnek DP Modeli-8 Lindo en iyi çözümü (x 1, x 2, x 3, x 4) = (40, 40, 25), (y 1, y 2, y 3, y 4) = (0, 10, 35, 0) ve toplam maliyet = $78450. 00 olarak verir. Üretim çizelgesi: M 1 M 2 M 3 M 4 Normal mesai (xt) 40 40 40 25 Fazla mesai (yt) 0 10 35 0 10 0 0 40 60 75 Envanter(it) Talep (dt) 10 0 25

Örnek DP Modeli-9 Bir bilgisayar şirketinde müşteri hizmetleri için deneyimli uzmana olan talep (adamsaat/ay) aşağıdaki gibidir: t Ocak Şub Mart Nis May dt 6000 7000 8000 9500 11000 Ocak ayı başında şirkette 50 deneyimli uzman vardır. Her uzman ayda 160 saat çalışabilir. Yeni bir uzmanı yetiştirmek için deneyimli uzmanlar 50 saat ayırmaktadır ve söz konusu uzmanın eğitimi bir ayda tamamlanmaktadır. Her deneyimli uzmana ayda $2000, her yeni uzmana ise ayda $1000 ödenmektedir. Her ay deneyimli uzmanların %5'i işten ayrılmaktadır. Şirket hem hizmet talebini karşılamak istemekte hem de maliyetleri enazlamak istemektedir. Sorunu çözmek için DP modeli kurunuz.

Örnek DP Modeli-9 Karar değişkenleri: xt = t ayında eğitilecek uzman sayısı İşlem yapabilmek için kullanılan diğer değişkenler ise yt = t. ayın başında şirketteki deneyimli uzman sayısı dt = t. ayın hizmet talebi Bu durumda min z = 2000(y 1+. . . +y 5)+1000(x 1+. . . +x 5) öyle ki 160 yt-50 xt ≥ dt for t = 1, . . . 5 y 1 = 50 yt =. 95 yt-1+xt-1 for t = 2, 3, 4, 5 xt, yt≥ 0

Örnek 10. Hesmak adında bir firma, A ve B markalarında iki tip hesap makinesi üretmektedir. Her bir A marka hesap makinesinin üretimi için 4 entegre ve iki dijital ekran ve B marka hesap makinesi için de 2 entegre ve 4 dijital ekran kullanılmaktadır. Kullanılabilir entegre miktarı 600 ve dijital ekran ise 480’dir. Üretilecek olan her bir A hesap makinesinin net karı 8 TL ve her bir B hesap makinesinin net karı 6 TL’dir. a)Firmanın karını maksimize edecek şekilde doğrusal programlama modelini kurunuz. b)Modeli grafik yöntemle çözünüz.

a) x= üretilecek A marka hesap makinesi adedi y= üretilecek B marka hesap makinesi adedi Z max= 8 x + 6 y 4 x + 2 y ≤ 600 2 x + 4 y ≤ 480 x≥ 0 y≥ 0 b) Modelin grafik yöntemle çözümü 4 x + 2 y ≤ 600 4 x + 2 y = 600 2 x + 4 y ≤ 480 2 x + 4 y = 480

4 x + 2 y = 600 2 x + 4 y = 480 Denklemleri çözümlenerek yukarıdaki tabloda görülen çözüm değerine ulaşılmaktadır. Böylece A hesap makinesinden 120 ve B hesap makinesinden 60 adet üretildiğinde kar maksimum olmaktadır ( kar 1320 TL )

Örnek 2. GÜBRECİ adında bir firma, nitrat ve fosfat maddelerinden oluşan karışık bir ürün üretmek istemektedir. Elde edilecek karışık ürün 50 kg ’lik paketler halinde satılacaktır. Araştırmalara göre, bir pakette en az 20 kg nitrat ve en fazla 40 kg fosfat olması gerekmektedir. Bir kg nitratın maliyeti 10 TL ve 1 kg fosfatın maliyeti ise 25 TL’dir. Firmanın amacı maliyeti en düşük olacak şekilde bir karışım ürün üretmektir. a)Firmanın maliyetini minimum yapacak şekilde doğrusal programlama modelini kurunuz. b)Modeli grafik yöntemle çözünüz.

a) x= karışımda kullanılacak nitrat miktarı y= karışımda kullanılacak fosfat miktarı Z min= 10 x + 25 y x + y = 50 x ≥ 20 y ≤ 40 ve x ≥ 0 y ≥ 0 ‘dır.

b)

TESEKKUR EDERIM YAVUZ DEMIRDOGEN