EFFICIENT AUCTIONS PARTHA DASGUPTA AND ERIC MASKIN QUARTERLY

















































- Slides: 49

EFFICIENT AUCTIONS PARTHA DASGUPTA AND ERIC MASKIN QUARTERLY JOURNAL OF ECONOMICS May 2000

INTRODUCTION n n Efficient auctions – auctions that put goods into the hands of the buyers who value them the most. Most of theoretical literature on auctions primarily concentrates on revenue-maximization.

Motivation n A leading rationale for the widespread privatization of state-owned assets in recent years is to enhance efficiency.

The Case of many buyers n n n If there a sufficiently large number of potential buyers, competition will render virtually any kind of auction approximately efficient. In practice, the number of serious bidders is often severely limited. For many properties sold in the FCC spectrum auctions, the number of bidders submitting realistic bids was as low as two or three.

Common values n n Common values - where one buyer’s valuation can depend on the private information of another buyer. Example: several wildcatters are bidding for the right to drill for oil on a given tract of land.

The principal contribution of this paper n n Show that the Vickrey auction can be generalized so as to attain efficiency even when there are common values. Show that this auction remains efficient regardless of the number of goods being sold, and of the nature of those goods, e. g. , whether they are substitutes or complements.

Formulation n n Suppose that there is a single unit of a good available for auction. There are n risk-neutral buyers. Buyer i observes a private real-valued Signal si. Let vi (s 1, . . . , sn) be buyer i’s expected valuation for the good, conditional on all the signals (s 1, . . . , sn).

Formulation (Cont. ) n n If buyer i is awarded the good and pays price p, his net payoff is vi (s 1 , . . . , sn ) – p Assume that, for all i, vi(·) is continuously differentiable in its arguments and that a higher signal value si corresponds to a higher valuation:

Example & Definition n n If vi(s 1 , . . . , sn ) = si, then this is an auction of private values. We call an auction efficient if, for all signal values (s 1, . . . , sn), the winner in equilibrium is buyer i such that vi(s 1 , . . . , sn ) ≥ vj(s 1 , . . . , sn ) for all j.

Familiar auction types n n n High-bid auction: The buyers submit sealed bids, the winner is the high bidder. Second-price (or Vickrey) auction: Has the same rules as the high-bid, except that the winner pays only the second-highest bid. English auction: The buyers call out bids publicly. The winner is the last buyer to bid, and he pays his bid.

High-bid auction n n Even with private values, the high-bid auction is not, in general, efficient. Example: s 1 is drawn from a continuous distribution on [0, 1] whereas s 2 is drawn (independently) from a continuous distribution on [0, 10]. The equilibrium bid functions (b 1(·), b 2(·)) satisfy b 1(1) = b 2(10), where b 2(·) is strictly increasing at s 2=10.

Second-price auction n n Is efficient in the case of private values. Not efficient in the case of common values !!

Second-price auction Example n n Suppose that there are three buyers, whose valuations are: v 1(s 1 , s 2 , s 3 ) = s 1 + ½ s 2 + ¼ s 3 v 2(s 1 , s 2 , s 3 ) = s 2 + ¼ s 1 + ½ s 3 v 3(s 1 , s 2 , s 3 ) = s 3 In a neighborhood of (s 1, s 2, s 3) = (1, 1, 1), efficient allocation of the good between buyers 1 and 2 depends on the value of s 3.

Direct revelation mechanisms n n n Each buyer i reports a signal value ŝi. The good is awarded to the buyer i for whom vi(ŝ 1, . . . , ŝn) ≥ maxi≠j vj(ŝ 1, . . . , ŝn). In equilibrium, ŝi equals the true value si.

Direct revelation mechanisms - Problems n It would require the mechanism designer (or auctioneer) to know the physical signal spaces S 1, S 2, and S 3 and the functional forms of the valuation functions v 1(·), v 2(·), and v 3(·). A strong assumption.

Condition on valuations n for all i and j≠i, n At any point where vi(s 1, . . . , sn) = vj(s 1, . . . , sn) = maxk vk(s 1, . . . , sn). The condition says that (if buyers i and j have equal and maximal valuations) buyer i’s signal must have a greater marginal effect on his own valuation than on that of buyer j.

Example to establish condition n n Two wildcatters are competing for the right to drill for oil on a given tract of land. Wildcatter 1 has a fixed cost of 1 and a marginal cost of 2. Wildcatter 2’s fixed cost is 2 and marginal cost is 1. Oil can be sold at a price of 4. Only wildcatter 1 performs a test, and discovers that the expected size of the oil reserve is s 1 units.

Example (cont. ) n n n The value functions are: v 1(s 1 , s 2) = (4 -2)s 1 - 1 = 2 s 1 - 1 v 2(s 1 , s 2) = (4 -1)s 1 - 2 = 3 s 1 – 2 Notice that Efficiency dictates that wildcatter 1 get the drilling rights if ½ < s 1 < 1 and that wildcatter 2 get the drilling rights if s 1 > 1.

Example (cont. 2) n n n Suppose that wildcatter 1 is given a reward R(ŝ 1) if he claims that there are ŝ 1 units of oil. If s 1 > s’ 1 > ½ , incentive compatibility and efficiency demand that R (s 1 ) ≥ 2 s 1 – 1 + R(s’ 1) 2 s’ 1 – 1 + R(s’ 1) ≥ R(s 1) And we get 2(s’ 1 - s 1) ≥ 0 contradiction.

Auctions with Two Buyers n n Instead of a single bid, we will have each buyer i report a bid function, where j ≠ i. We can interpret as buyer i’s bid if the other buyer’s valuation turns out to be vj.

Find a fixed point n n Given the bid functions let us look for a fixed point, i. e. , a pair (v° 1, v° 2) such that Buyer i is the winner

Bidding truthfully n n To see that this allocation rule is the ‘‘right’’ one, consider what happens when buyers bid ‘‘truthfully. ’’ That is, if buyer 1’s signal value is s 1, the truthful bid function is b 1(·) such that b 1(v 2(s 1 , s’ 2)) = v 1(s 1 , s’ 2) for all s’ 2. Similarly, b 2(v 1(s’ 1 , s 2)) = v 2(s’ 1 , s 2) for all s’ 1.

Bidding truthfully (cont. ) n n Observe that (v° 1, v° 2) = (v 1(s 1 , s 2) , v 2(s 1 , s 2)) is a fixed point of the mapping (v 1, v 2) (b 1(v 2) , b 2(v 1)) This means that, if buyers bid truthfully, our allocation rule ensures that buyer 1 wins if and only if v 1(s 1, s 2) > v 2(s 1, s 2).

Example of two fixed points n n v 1(s 1, s 2) = s 1² + s 1 s 2 – s 2² + s 1 - 2 s 2 + 24 v 2(s 1, s 2) = s 2² + s 1 s 2 – s 1² - 9 s 1 + 13 If (s 1, s 2) = (2, 3), then one fixed point is (v 1(2, 3) , v 1(2, 3)) = (21, 6) However, for these signal values, (v 1(2, 4) , v 2(1, 3)) = (14, 15) also constitutes a fixed point, because vi(2, 4) = vi(1, 3), and so v 2(1, 3) = b 2(v 1(1, 3)), and v 1(2, 4) = b 1(v 2(2, 4)).

Stronger conditions to ensure unique fixed point n for all i and j≠i, At any point. n n Note that And so, we obtain and vice versa. for all v 1

Winning’s buyer payment n n It remains to establish that there exists a payment scheme that induces truthful bidding. The way that the Vickrey auction induces truthfulness in the private-values case is to make a winning buyer’s payment equal to the lowest bid that he could have made for which he would still have won the auction.

Winning’s buyer payment (cont. ) n Try to adhere to this principle means that, if buyer 1 is the winner, then he should pay where n This is because if buyer 1 were restricted to constant bids, v*1 would be the lowest such bid for which buyer 1 would still win the auction.

Incentive to bid truthfully n n If buyer 1 wins, his payoff is v 1(s 1, s 2) – b 2(v*1) where v*1 = b 2(v*1). To see that buyer 1 has an incentive to bid truthfully in equilibrium, it suffices to show that if buyer 1 sets then he wins if and only if his payoff is positive.

Proof of equilibrium n n (*) The payoff is positive iff for any v’ 1 From the intermediate value theorem, there exists a value of v’ 1 such that

Proof of equilibrium (cont. ) n n Hence, (*) holds if and only if v 1(s 1, s 2) - v*1 > b 2(v 1(s 1, s 2)) - b 2(v*1). But v*1 = b 2(v*1) , and b 2(v 1(s 1, s 2)) = v 2(s 1, s 2) (**) Hence, (*) holds if and only if v 1(s 1, s 2) > v 2(s 1, s 2). But, when he is truthful, buyer 1 wins if and only if (**) holds. Hence, if buyer 1 bids truthfully, (*) is indeed positive if and only if buyer 1 wins.

To summarize n Consider the two-buyer auction in which, for i = 1, 2, n buyer i reports i≠j and a contingent bid function that satisfy n n a fixed point (v° 1, v° 2) is taken, and the winner is determined. Winner i pays

To summarize (cont. ) n This auction is efficient: n n It is an equilibrium for each buyer i to bid truthfully. If both buyers do so, the auction results in an efficient outcome.

Remark 1 n n n It may seem very demanding to insist that a buyer make his bid a function of the other buyer’s valuation. Indeed, suppose that buyer 1 knew nothing about the nature of v 2(·), He could, make an uncontingent bid b 1(·) b 1. In this sense, having buyers report contingent bids should be viewed as giving them an opportunity to express their interdependencies.

Remark 2 n n Some degree of common knowledge about valuation functions is needed to ensure that players can calculate equilibrium. Why we do not go ‘‘all the way’’ and have each buyer i report a pair of valuation functions (vˆ1(·), vˆ2(·)) and then n (i) use a ‘‘direct revelation’’ mechanism, in which each buyer reports his signal value and these are then plugged into the reported valuation functions. (ii) or punish buyers in some way if their reports disagree.

Remark 2 (cont. ) n n n There is a difficulty, however, with having buyer 1 report vˆ2(·), namely, he may not even know what buyer 2’s physical signal space. Notice that there is no contradiction in supposing that buyer 1 does not know v 2(·) but does know v*2. The ability of buyer i to calculate v*j can be thought of as the weakest hypothesis that ensures efficiency in equilibrium.

Auctions with More than Two Buyers n n n Each buyer i (i = 1, . . . , n) submits a bid correspondence where A fixed point (v° 1, . . . , v°n) is calculated so that for all i. if v°i ≥ maxj≠i v°j , the good is awarded to buyer i.

Auctions with More than Two Buyers (cont. ) n n n If buyer i is the winner, he makes a payment maxj≠iv*j , where (v*1, …, iv*n) is a vector such that v*j = maxj≠iv*j and for all k≠i. What if there are multiple fixed points ? What if there are multiple payment points ?

Conditions to ensure efficiency equilibrium n n (i) For all i, for all s-i S–i , there exists s'i Si such that vi(s'i, s-i) > maxj≠iv(s'i, s-i). (ii) for all m=1, …, n

Proposition n n Assume that, for all i = 1, . . . , n, buyer i’s valuation function satisfies (i), and that buyers’ valuation functions collectively satisfy (ii), then it is an equilibrium for each buyer i to bid truthfully. Moreover, if buyers are truthful, the auction is efficient.

Example with three users n n n (i) v 1(s 1 , s 2 , s 3 ) = s 1 + ½ s 2 + ¼ s 3 (ii) v 2(s 1 , s 2 , s 3 ) = s 2 + ¼ s 1 + ½ s 3 (iii) v 3(s 1 , s 2 , s 3 ) = s 3 Buyer 3’s valuation does not depend on s 1 and s 2 and so, given s 3, his truthful bid function b 3(v 1, v 2) = s 3. b 1(v 2, v 3) = s 1 + ½ (v 2 – ¼ s 1 – ½ v 3) + ¼ v 3 = 7/8 s 1 + ½ v 2. b 2(v 1, v 3) = 7/8 s 2 + ¼ v 1 + 7/16 v 3

Example (cont. ) n Suppose for example, that s 1 = s 2 =1 and that s 3 is either slightly less than 1. Then buyer 1 is the winner, and he should pay v*1 = b 2(v*1, v*3) = 7/ + ¼ v* + 7/ v* 8 1 16 3 i. e. , v*1 = 7/6 + 7/12 s 3 Hence, buyer 1’s net payoff is (1 + ½ + ¼ s 3 ) – (7/6 + 7/12 s 3 )

Multidimensional Signals n n Example: There are two wildcatters competing for the right to drill for oil on a tract of land consisting of an eastern and western region. Wildcatter 1 has a (fixed) cost of drilling c 1, which is private information. She also performs a private test that tells her that the expected quantity of oil in the eastern region is q 1. Wildcatter 2 has fixed cost c 2 and expected quantity q 2 in the western region.

Multidimensional Signals(cont) n n wildcatter 1’s information can be summarized, from her own standpoint, by the onedimensional signal t 1 =q 1 - c 1. However, t 1 is not an adequate summary of 1’s information from wildcatter 2’s standpoint.

Proposition n If there exist signal values s i , s i and s -i such that vi(s i, ·) = vi(s i , ·), but arg maxj vj(s i, , s -i) ≠ arg maxj vj(s i, , s -i) then there is no efficient auction with regular equilibria.

Multiple goods n n n Each buyer has valuation for every possible set of goods. For each subset of goods, the buyer report bid function. Again we will look for fixed points.

Problem with multiple goods n n Vickrey auctions for multiple goods are sometimes criticized as demanding too much information of a buyer: he is asked to submit a bid for each possible combination of goods. Further-more, in our common-values setting, these bids must be made contingent on all other buyers’ valuations.

An answer n n n In our view, these criticisms are overblown. A buyer could be permitted to submit bids only on those combinations of goods he is potentially interested in. Furthermore, he could choose to make his bids contingent only on those other buyers’ valuations that, he believes, share a significant common component with his own valuation.

An open question n there at least two important advantages that an English auction could have over a generalized Vickrey auction: n n at any instant, a buyer in an English auction need make only a binary decision: whether or not to drop out. Back to the 3 buyers example… In the English auction, buyer 3’s true signal value can be inferred even though he does not win. In the generalized Vickrey auction, by contrast, buyer 3 must truthfully bid b 3(v 1, v 2) in order for s 3 to be revealed.

An open question (cont. ) n Thus, on both counts, we regard finding an appropriate ‘‘English’’ auction (i. e. , a dynamic auction with binary decisions at each instant) counterpart to our Vickrey auction with multiple goods as a leading topic for further research.
 Productively efficient vs allocatively efficient
Productively efficient vs allocatively efficient Allocative efficiency
Allocative efficiency Productively efficient vs allocatively efficient
Productively efficient vs allocatively efficient Productively efficient vs allocatively efficient
Productively efficient vs allocatively efficient Productive inefficiency and allocative inefficiency
Productive inefficiency and allocative inefficiency Mrinal dasgupta
Mrinal dasgupta Manisha dasgupta
Manisha dasgupta Amartya dasgupta
Amartya dasgupta Nairanjana dasgupta
Nairanjana dasgupta Cisco ethernet oam
Cisco ethernet oam Diff
Diff Partha kanuparthy
Partha kanuparthy Partha kanuparthy
Partha kanuparthy Klaibyam ma sma gamah partha
Klaibyam ma sma gamah partha Partha sarker
Partha sarker Partha dutta rpi
Partha dutta rpi Partha kanuparthy
Partha kanuparthy Snurrande del i maskin
Snurrande del i maskin Split maskin
Split maskin Menneske-maskin interaksjon
Menneske-maskin interaksjon Mjukglassmaskin leasing
Mjukglassmaskin leasing Carnotcykeln
Carnotcykeln Maskin
Maskin Christys angels auctions
Christys angels auctions Type of auctions
Type of auctions Baystate auctions
Baystate auctions Kista bus sales
Kista bus sales Regretnet
Regretnet Ecommerce online auctions
Ecommerce online auctions Forward auction
Forward auction Anderson auctions
Anderson auctions Play auctions
Play auctions Russell quarterly economic and market review
Russell quarterly economic and market review Russell quarterly economic and market review
Russell quarterly economic and market review Quarterly business review examples
Quarterly business review examples Access securepak californiaqp
Access securepak californiaqp Gantt chart quarterly template
Gantt chart quarterly template Quarterly business review ppt
Quarterly business review ppt Kpi templates
Kpi templates Ecrq author guidelines
Ecrq author guidelines Quarterly business review templates
Quarterly business review templates Quarterly business review
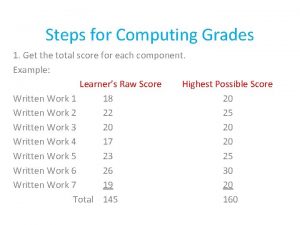
Quarterly business review Grading system deped
Grading system deped Fidelity quarterly market update q1 2018
Fidelity quarterly market update q1 2018 Experian automotive quarterly briefing
Experian automotive quarterly briefing Wv doc quarterly package program
Wv doc quarterly package program Arrangement of people in an organization
Arrangement of people in an organization Examples of explicit instruction
Examples of explicit instruction Using the body in an efficient and careful way is
Using the body in an efficient and careful way is Irregular modifiers
Irregular modifiers