EE 313 Linear Systems and Signals Fall 2010

EE 313 Linear Systems and Signals Fall 2010 Laplace Transform Prof. Brian L. Evans Dept. of Electrical and Computer Engineering The University of Texas at Austin Initial conversion of content to Power. Point by Dr. Wade C. Schwartzkopf

Forward Laplace Transform • Decompose a signal f(t) into complex sinusoids of the form es t where s is complex: s = s + j 2 pf • Forward (bilateral) Laplace transform f(t): complex-valued function of a real variable t F(s): complex-valued function of a complex variable s • Bilateral means that the extent of f(t) can be infinite in both the positive t and negative t direction (a. k. a. two-sided) 2

Inverse (Bilateral) Transform • Inverse (Bilateral) Transform is a contour integral which represents integration over a complex region– recall that s is complex c is a real constant chosen to ensure convergence of the integral • Notation F(s) = L{f(t)} f(t) = L-1{F(s)} variable t implied for L variable s implied for L-1 3

Laplace Transform Properties • Linear or nonlinear? • Linear operator f(t) L F(s) 4

Laplace Transform Properties • Time-varying or time-invariant? This is an odd question to ask because the output is in a different domain than the input. 5

Example 6

Convergence • The condition Re{s} > -Re{a} is the region of convergence, which is the region of s for which the Laplace transform integral converges • Re{s} = -Re{a} is not allowed (see next slide) 7

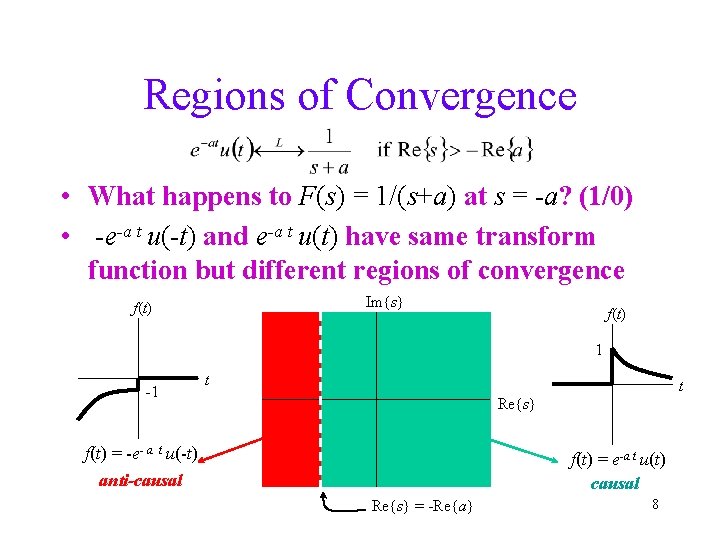
Regions of Convergence • What happens to F(s) = 1/(s+a) at s = -a? (1/0) • -e-a t u(-t) and e-a t u(t) have same transform function but different regions of convergence Im{s} f(t) 1 -1 t t Re{s} f(t) = -e- a t u(-t) f(t) = e-a t u(t) causal anti-causal Re{s} = -Re{a} 8

Review of 0 and + 0 • d(t) not defined at t = 0 but has unit area at t = 0 • 0 - refers to an infinitesimally small time before 0 • 0+ refers to an infinitesimally small time after 0 9

Unilateral Laplace Transform • Forward transform: lower limit of integration is 0 - (i. e. just before 0) to avoid ambiguity that may arise if f(t) contains an impulse at origin • Unilateral Laplace transform has no ambiguity in inverse transforms because causal inverse is always taken: No need to specify a region of convergence Disadvantage is that it cannot be used to analyze noncausal systems or noncausal inputs 10

Existence of Laplace Transform • As long as e-s t decays at a faster rate than rate f(t) explodes, Laplace transform converges for some M and s 0, there exists s 0 > s to make the Laplace transform integral finite We cannot always do this, e. g. does not have a Laplace transform 11

Key Transform Pairs 12

Key Transform Pairs 13

Fourier vs. Laplace Transform Pairs Assuming that Re{a} > 0 14