EE 313 Linear Systems and Signals Fall 2010

EE 313 Linear Systems and Signals Fall 2010 Fourier Transform Properties Prof. Brian L. Evans Dept. of Electrical and Computer Engineering The University of Texas at Austin Initial conversion of content to Power. Point by Dr. Wade C. Schwartzkopf

Duality • Forward/inverse transforms are similar rect(t/t) t sinc(w t / 2) • Example: t sinc(t t/2) 2 p rect(-w/t) t sinc(t t /2) 2 p rect(w/t) Apply duality rect(·) is even f(t) 1 -t/2 0 t F(w) t/2 t w 6 p t 4 p t -2 p t 0 2 p t 4 p t 6 p t 2

Scaling • Given and that a 0 |a| > 1: compress time axis, expand frequency axis |a| < 1: expand time axis, compress frequency axis • Extent in time domain is inversely proportional to extent in frequency domain (a. k. a bandwidth) f(t) is wider spectrum is narrower f(t) is narrower spectrum is wider 3

Shifting in Time • Shift in time Does not change magnitude of the Fourier transform Shifts phase of Fourier transform by -wt 0 (so t 0 is the slope of the linear phase) • Derivation Let u = t – t 0, so du = dt and integration limits stay same 4

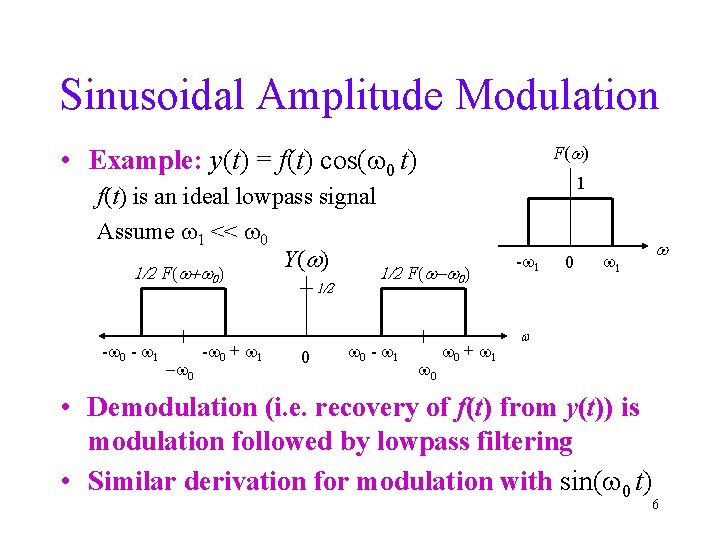
Sinusoidal Amplitude Modulation 5

Sinusoidal Amplitude Modulation F(w) • Example: y(t) = f(t) cos(w 0 t) f(t) is an ideal lowpass signal Assume w 1 << w 0 Y(w) 1/2 F(w+w 0) -w 0 - w 1 w 0 -w 0 + w 1 1/2 0 1 1/2 F(w-w 0) w 0 - w 1 w 0 + w 1 -w 1 0 w w 1 w • Demodulation (i. e. recovery of f(t) from y(t)) is modulation followed by lowpass filtering • Similar derivation for modulation with sin(w 0 t) 6

Frequency-shifting Property 7

Time Differentiation Property • Conditions f(t) 0 when |t| f(t) is differentiable • Derivation of property: Given f(t) F(w) 8

Time Integration Property • Example: 9

Summary • Definition of Fourier Transform • Two ways to find Fourier Transform Use definition Use transform pairs and properties 10