ECE 667 Synthesis and Verification of Digital Systems

ECE 667 Synthesis and Verification of Digital Systems Exact Two-level Minimization Quine-Mc. Cluskey Procedure Slides adopted (with permission) from A. Kuehlmann, UC Berkeley, 2003 1

Outline • QM Theorem • Generating all primes – Single output functions – Multiple output functions • Setting up a covering table • Solving the Unate Covering Problem – Reduction rules – Solving cyclic core ECE 667 - Synthesis & Verification 2

Quine-Mc. Cluskey Theorem (Quine): There is a minimum cover that is prime Proof: Consider a minimum cover that is not prime. Each non-prime implicant can be replaced by a prime implicant that covers it. Thus the resulting set of implicants is a cover and has the same cardinality as the original cover. Hence, there is a minimum cover that is prime. • Given initial cover for F = (f, d, r), find a minimum cover G of primes where: f G f+d G is a prime cover of F ; f = on-set, r = off-set, d = don’t care set ECE 667 - Synthesis & Verification 3

Quine-Mc. Cluskey Procedure (Exact) Q-M Procedure: 1. Generate all primes (f+d), call it {Pi} 2. Generate all minterms of (f+d), call it {mi} 3. Build a covering (prime implicant) matrix B, where Bij = 1 if mi Pj = 0 otherwise 4. Solve the minimum column covering problem for B (unate covering problem), UCP. ECE 667 - Synthesis & Verification 4

Example (on set) (don’t care set) x y x z xy xy x y z w y’ Covering table w zw y’ w x’z’ x’y’z’w’ zw x’y z’w z w x y’z’w Primes: y’ + w + x’z’ ECE 667 - Synthesis & Verification x’y zw 5

Covering Table Minterms of f {p 1 y’ p 2 w p 3} Primes of (f+d) x’z’ x’y’ z’w’ x’y z’w x y’ z’w x’y z w Row singleton (essential minterm) Essential prime Recall: An essential prime is any prime that uniquely covers a minterm of f. Solution: {p 1, p 2} y + w is minimum prime cover. (Also w + x z) Possible approach (SAT): (p 1+p 3)(p 2 +p 3)(p 1+p 2)p 2 ECE 667 - Synthesis & Verification 6

Table reduction - Column Dominance Definition: A column P 1 whose 1 -entries are a superset of another column P 2 is said to dominate P 2. P 1 P 2 Example: P 1 dominates P 2 (it has 1 everywhere P 2 has) 1 0 1 0 0 1 We can remove dominated column P 2 since P 1 covers all those rows and more. We would never choose P 2 in a minimum cover since it can always be replaced by P 1. ECE 667 - Synthesis & Verification 7

Row Dominance and equality Definition: A row m 1 whose set of primes contains the set of primes of row m 2 is said to dominate m 2. . Example: m 1 m 2 011110 011010 Dominating row m 1 dominates m 2 : it has 1 everywhere m 2 has 1 We can remove dominating row m 1: any prime that covers m 2 also covers m 1 (covered automatically). Row Equality: • In practice, many rows are identical. That is there exist minterms that are contained in the same set of primes. ECE 667 - Synthesis & Verification 8

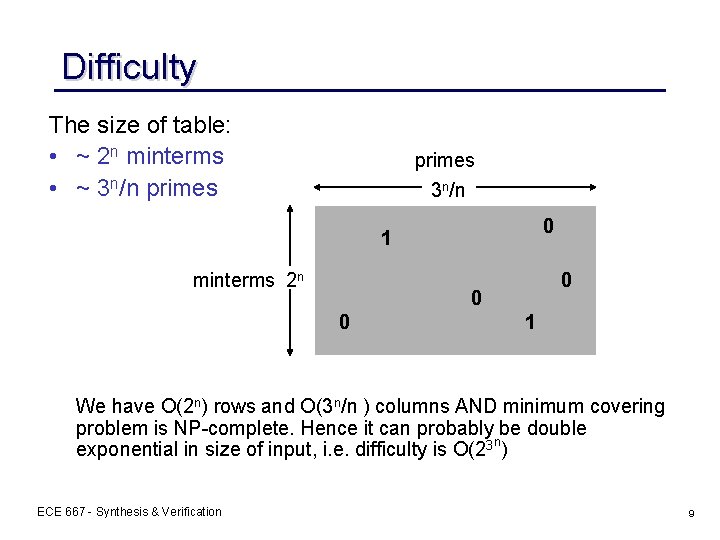
Difficulty The size of table: • ~ 2 n minterms • ~ 3 n/n primes 3 n/n 0 1 minterms 2 n 0 0 0 1 We have O(2 n) rows and O(3 n/n ) columns AND minimum covering problem is NP-complete. Hence it can probably be double exponential in size of input, i. e. difficulty is O(23 n) ECE 667 - Synthesis & Verification 9

Pruning the Covering Table 1. Remove all rows covered by essential primes (columns in row singletons). Put these primes in the cover G. 2. Group identical rows together and remove dominating rows. 3. Remove dominated columns. For equal columns, keep one prime to represent them. 4. Newly formed row singletons define essential primes. 5. Go to step 1 if covering table decreased. • • The resulting reduced covering table is called the cyclic core. This has to be solved (unate covering problem). A minimum solution is added to G (set of essential primes). The resulting G is a minimum cover. ECE 667 - Synthesis & Verification 10

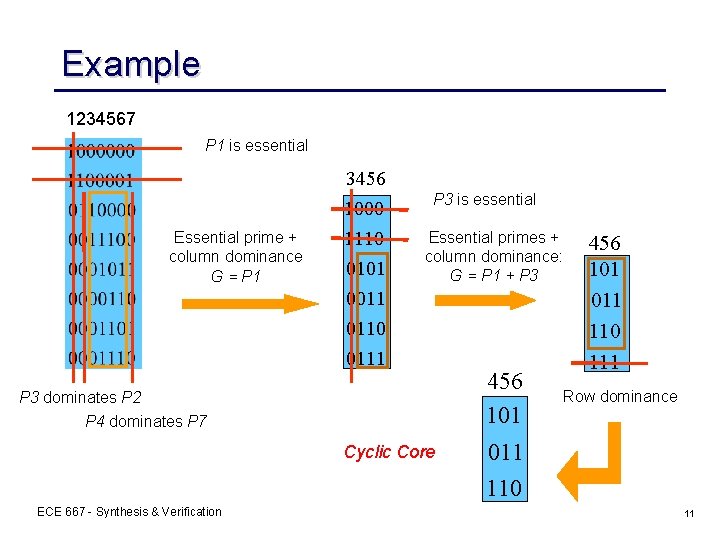
Example 1234567 P 1 is essential 3456 Essential prime + column dominance G = P 1 1000 1110 0101 0011 0110 0111 P 3 is essential Essential primes + column dominance: G = P 1 + P 3 dominates P 2 P 4 dominates P 7 Cyclic Core 456 101 011 110 111 Row dominance 011 110 ECE 667 - Synthesis & Verification 11

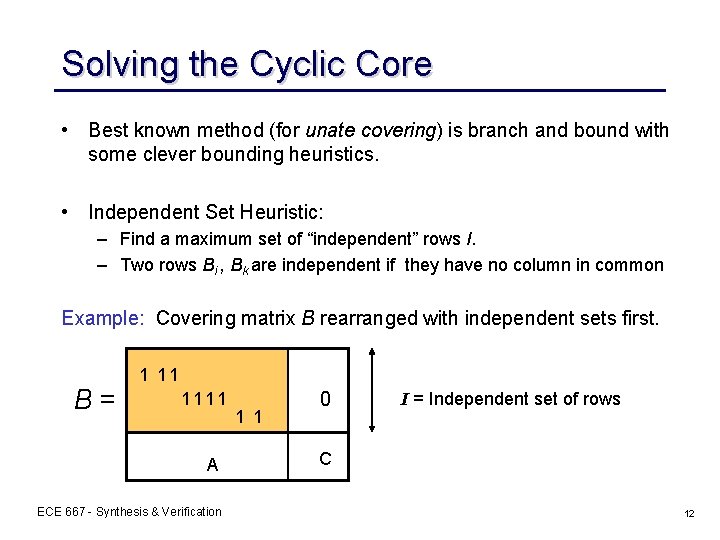
Solving the Cyclic Core • Best known method (for unate covering) is branch and bound with some clever bounding heuristics. • Independent Set Heuristic: – Find a maximum set of “independent” rows I. – Two rows Bi , Bk are independent if they have no column in common Example: Covering matrix B rearranged with independent sets first. B= 1 11 1111 A ECE 667 - Synthesis & Verification 1 1 0 I = Independent set of rows C 12

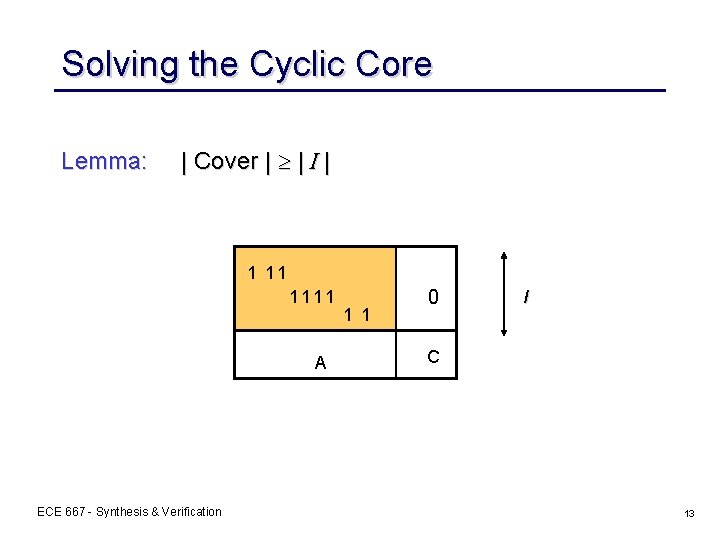
Solving the Cyclic Core Lemma: | Cover | | I | 1 11 1111 A ECE 667 - Synthesis & Verification 1 1 0 I C 13

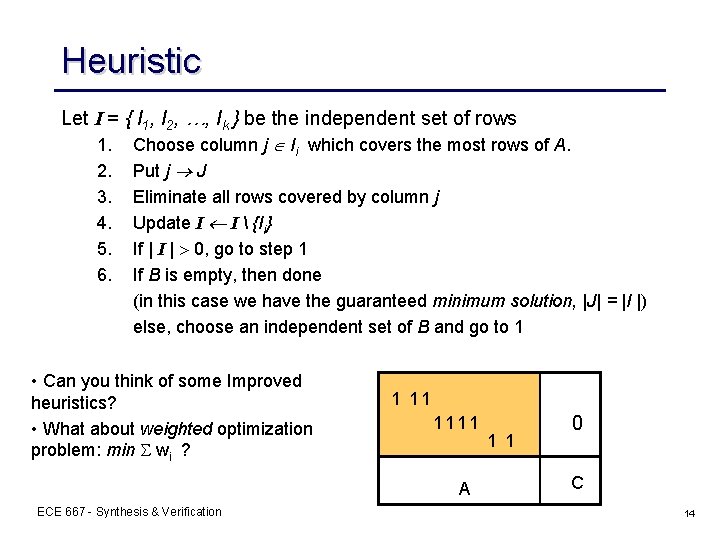
Heuristic Let I = { I 1, I 2, …, Ik } be the independent set of rows 1. Choose column j Ii which covers the most rows of A. 2. Put j J 3. 4. 5. 6. Eliminate all rows covered by column j Update I I {Ii} If | I | 0, go to step 1 If B is empty, then done (in this case we have the guaranteed minimum solution, |J| = |I |) else, choose an independent set of B and go to 1 • Can you think of some Improved heuristics? • What about weighted optimization problem: min wi ? 1 11 1111 A ECE 667 - Synthesis & Verification 1 1 0 C 14

Branch and Bound Algorithm (generic) ECE 667 - Synthesis & Verification 15

Generating Primes - single output func. Tabular method (based on consensus operation): • • Start with all minterm canonical form of F Group pairs of adjacent minterms into cubes Repeat merging cubes until no more merging possible; mark ( ) + remove all covered cubes. Result: set of primes of f. Example: F = x’ y’ + w x y + x’ y z’ + w y’ z ECE 667 - Synthesis & Verification F = x’ y’ + w x y + x’ y z’ + w y’ z w’ x’ y’ z’ w’ x’ y’ z w’ x’ y z’ w x’ y’ z w x’ y z’ w x y’ z wxyz w’ x’ y’ w’ x’ z’ x’ y’ z x’ y z’ w x’ y’ w x’ z’ w y’ z w y z’ wxy wxz x’ y’ x’ z’ 16

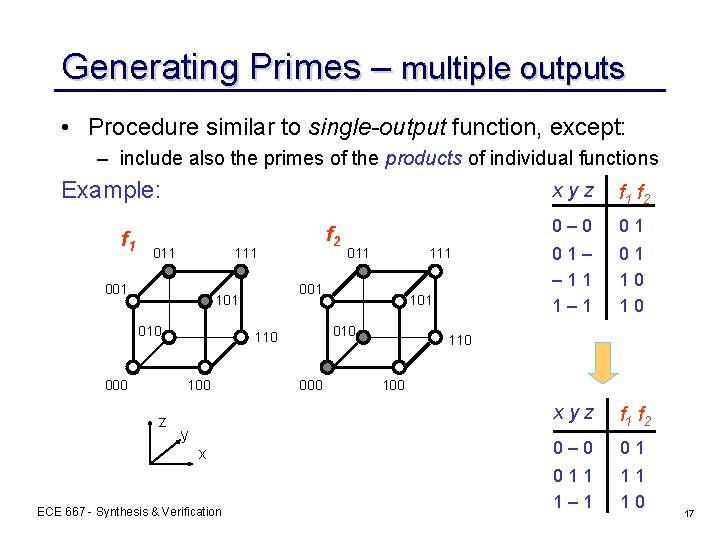
Generating Primes – multiple outputs • Procedure similar to single-output function, except: – include also the primes of the products of individual functions Example: f 1 011 111 001 010 z y x ECE 667 - Synthesis & Verification 111 101 010 100 011 001 101 000 f 2 000 xyz f 1 f 2 0– 0 01 01– – 11 1– 1 01 10 10 xyz f 1 f 2 0– 0 01 011 1– 1 11 10 100 17

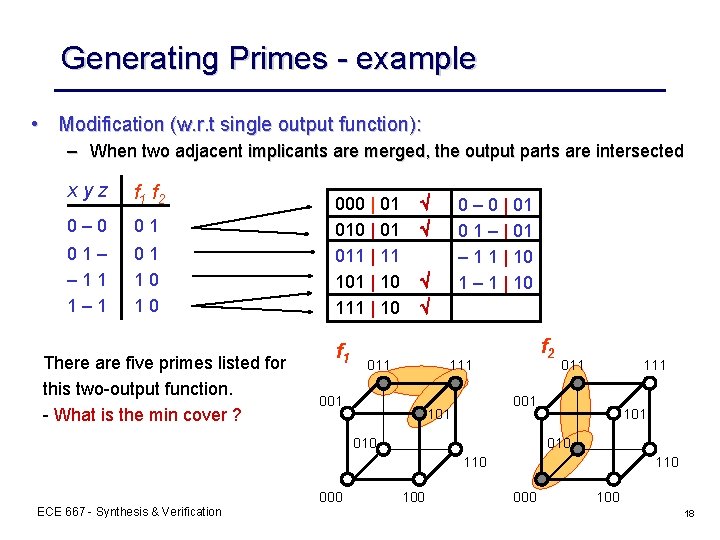
Generating Primes - example • Modification (w. r. t single output function): – When two adjacent implicants are merged, the output parts are intersected xyz f 1 f 2 0– 0 01 01– – 11 1– 1 01 10 10 There are five primes listed for this two-output function. - What is the min cover ? 000 | 01 011 | 11 101 | 10 111 | 10 f 1 0 – 0 | 01 0 1 – | 01 – 1 1 | 10 1 – 1 | 10 011 f 2 111 001 011 111 001 101 010 110 ECE 667 - Synthesis & Verification 000 110 000 18

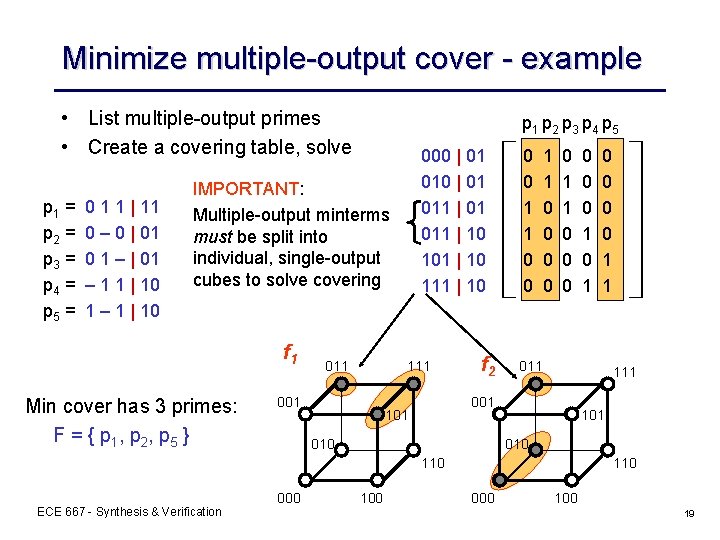
Minimize multiple-output cover - example • List multiple-output primes • Create a covering table, solve p 1 = p 2 = p 3 = p 4 = p 5 = 0 1 1 | 11 0 – 0 | 01 0 1 – | 01 – 1 1 | 10 1 – 1 | 10 p 1 p 2 p 3 p 4 p 5 000 | 01 011 | 10 101 | 10 111 | 10 IMPORTANT: Multiple-output minterms must be split into individual, single-output cubes to solve covering f 1 Min cover has 3 primes: F = { p 1, p 2, p 5 } 011 111 001 f 2 0 0 1 1 0 010 111 101 010 110 ECE 667 - Synthesis & Verification 000 0 0 1 1 011 001 101 0 0 0 1 100 110 000 19

Summary Q-M: 1. Generate cover of all primes 2. Make G irredundant (in optimum way) Note: Q-M is exact i. e. , it gives an exact minimum Heuristic Methods: 1. Generate (somehow) a cover of F using some of the primes 2. 3. Make G irredundant (maybe not optimally) Keep best result - try again (go to 1) ECE 667 - Synthesis & Verification 20