Dr Kafu WONG ECON 1003 Analysis of Economic
















- Slides: 22

Dr. Ka-fu WONG ECON 1003 Analysis of Economic Data Ka-fu Wong © 2003 Lab 1 -1

Counting the cards n We are interested in knowing the number of cards in box. n We only need to do to obtain a reasonable estimate of cards in the box – allowing for errors of counting or estimation. Ka-fu Wong © 2003 2

Two examples n n Example #1: The box contains only a small number of cards. Example #2: The box contains a lot of cards that will take days to count. Ka-fu Wong © 2003 3

In-class Lab Capture/Re-capture GOAL: 1. Illustrate that how to estimate the population size when the cost of counting all individuals is prohibitive. 2. Illustrate how easy and intuitive statistics could be. Statistics need not be completely deep, murky, and mysterious. Our common sense can help us to negotiate our way through the course. Ka-fu Wong © 2003 4

History and examples of capture / recapture method n Capture-recapture methods were originally developed in the wildlife biology to monitor the census of bird, fish, and inset populations (counting all individuals is prohibitive). Recently, these methods have been utilized considerably in the areas of disease and event monitoring. n http: //www. pitt. edu/~yuc 2/cr/history. htm Ka-fu Wong © 2003 5

The fish example n Estimating the number of fish in a lake or pond. n C fish is caught, tagged, and returned to the lake. n Later on, R fish are caught and checked for tags. Say T of them have tags. n The numbers C, R, and T are used to estimate the fish population. Ka-fu Wong © 2003 6

Cards in a box n The objective is to estimate the number of fish (represented by black cards) in a box. n Capture one handful of fish (black cards). Count them and call it C. Mark the fish by replacing the black cards with red cards. Put them back into the box. n Capture another handful of fish (cards). Count the total number of fish or cards (R) and the number of marked fish or red cards (T). n Based on this information, n How to obtain a reasonable estimate of the number of fish or cards in the box? Ka-fu Wong © 2003 7

Cards in a box n We know that C/N ≈ T/R n Hence, a simple estimate is CR/T n C= the number of fish or cards captured in the first round. n R= the total number of fish or cards captured in the second round. n T= the number of marked fish or red cards captured in the second round. Ka-fu Wong © 2003 8

Simulations to see the properties of this proposed estimator n How good is the proposed estimator? n To see the properties of this proposed estimator, I have use MATLAB to simulation our Capturerecapture experiment with different numbers of capture (C) and different numbers of recapture (R), relative to the total number of fish in the pond. n Throughout, n N=500 and n 1000 simulations Ka-fu Wong © 2003 9

Simulation design – via MATLAB n Individual simulation experiment: n Create 500 “black” fish, labelled 1 to 500. n Capture a random sample of C fish, mark them by converting their label to zero (i. e. , red fish). n Capture another random sample of R fish. Count the number of marked fish in the sample. Call it T. n Compute the estimate as CR/T. n If T=0, we are in trouble. Such experiments with T=0 are dropped. n Repeat this experiment 1000 times. Hence, we have 1000 estimates. n Compute the mean and standard deviation of these 1000 estimates. Ka-fu Wong © 2003 10

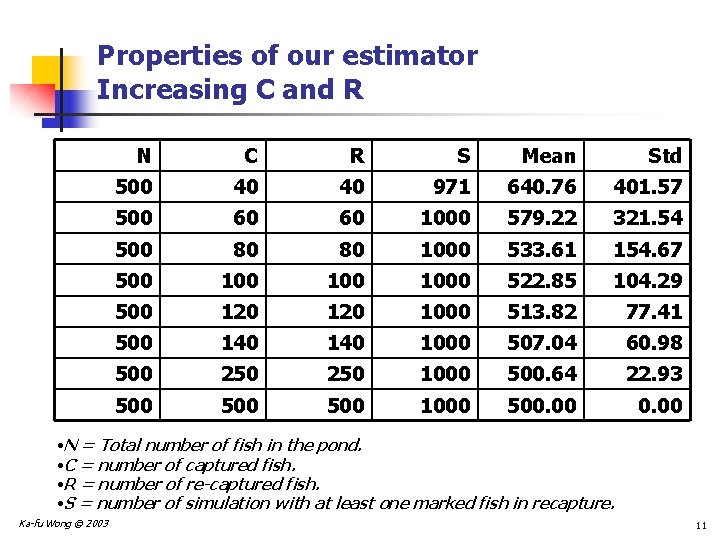
Properties of our estimator Increasing C and R N C R S Mean Std 500 40 40 971 640. 76 401. 57 500 60 60 1000 579. 22 321. 54 500 80 80 1000 533. 61 154. 67 500 100 1000 522. 85 104. 29 500 120 1000 513. 82 77. 41 500 140 1000 507. 04 60. 98 500 250 1000 500. 64 22. 93 500 500 1000 500. 00 • N = Total number of fish in the pond. • C = number of captured fish. • R = number of re-captured fish. • S = number of simulation with at least one marked fish in recapture. Ka-fu Wong © 2003 11

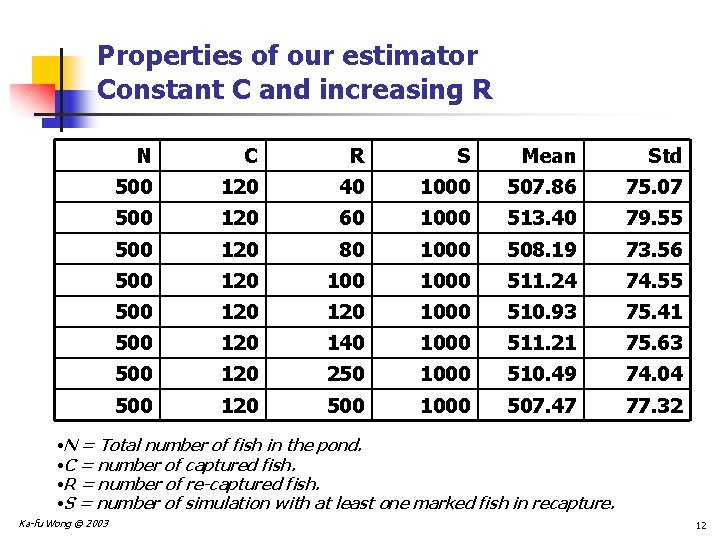
Properties of our estimator Constant C and increasing R N C R S Mean Std 500 120 40 1000 507. 86 75. 07 500 120 60 1000 513. 40 79. 55 500 120 80 1000 508. 19 73. 56 500 120 1000 511. 24 74. 55 500 120 1000 510. 93 75. 41 500 120 140 1000 511. 21 75. 63 500 120 250 1000 510. 49 74. 04 500 120 500 1000 507. 47 77. 32 • N = Total number of fish in the pond. • C = number of captured fish. • R = number of re-captured fish. • S = number of simulation with at least one marked fish in recapture. Ka-fu Wong © 2003 12

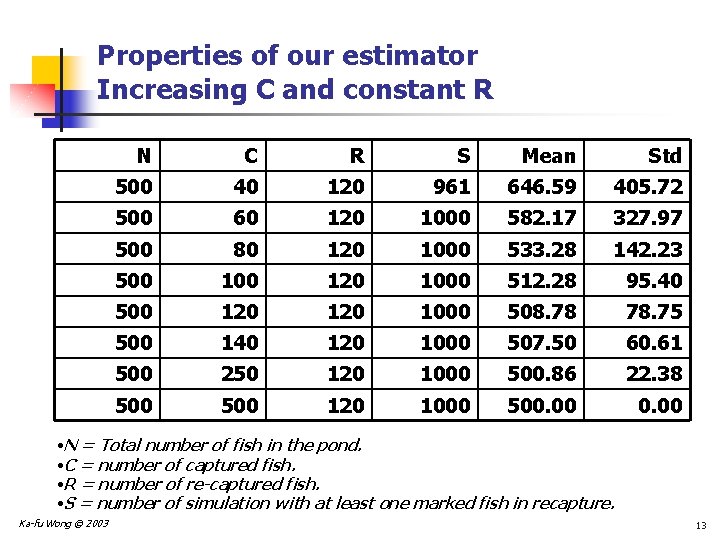
Properties of our estimator Increasing C and constant R N C R S Mean Std 500 40 120 961 646. 59 405. 72 500 60 120 1000 582. 17 327. 97 500 80 120 1000 533. 28 142. 23 500 120 1000 512. 28 95. 40 500 120 1000 508. 78 78. 75 500 140 120 1000 507. 50 60. 61 500 250 120 1000 500. 86 22. 38 500 120 1000 500. 00 • N = Total number of fish in the pond. • C = number of captured fish. • R = number of re-captured fish. • S = number of simulation with at least one marked fish in recapture. Ka-fu Wong © 2003 13

Conclusion from the simulations n The proposed estimator generally overestimate the number of fish in pond, i. e. , estimate is larger than the true number of fish in pond. n That is, there is a bias. n Holding R constant, increasing the number of capture (C) helps: n Bias is reduced, i. e. , Mean is closer to the true population n The estimator is more precise, i. e. , standard deviation of the estimator is smaller. n Holding C constant, increasing the number of recapture (R) does not help: n Bias is more or less unchanged. n The precision of the estimator is more or less unchanged. Ka-fu Wong © 2003 14

Additional issues n Our proposed estimator is good enough but it can be better. Alternative estimators have been developed to reduce or eliminate the bias of estimating N. n For instance, Seber (1982, p. 60) suggests an estimator of N (C+1)(R+1)/(T+1) – 1 (Note that our proposed formula is CR/T. ) Seber, G. (1982): The Estimation of Animal Abundance and Related Parameters, second edition, Charles. Ka-fu Wong © 2003 15

Simulations to see the properties of this modified estimator n How good is the modified estimator? n To see the properties of this modified estimator, we repeat the above simulation exercise with this new formula. (C+1)(R+1)/(T+1) – 1 Ka-fu Wong © 2003 16

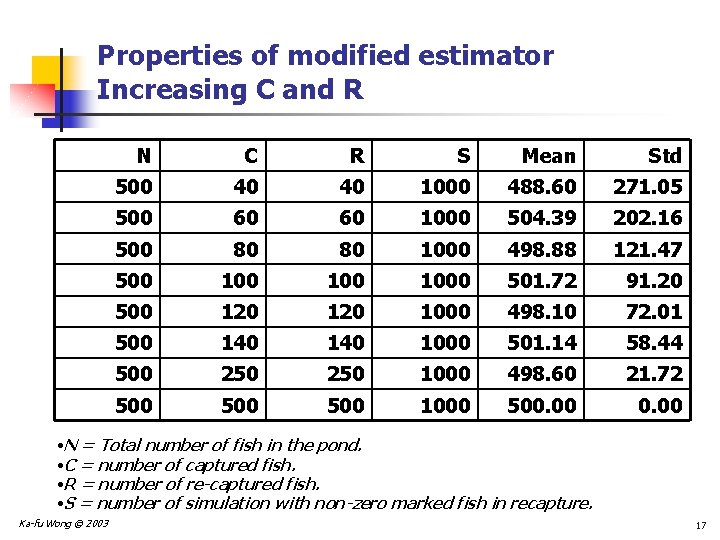
Properties of modified estimator Increasing C and R N C R S Mean Std 500 40 40 1000 488. 60 271. 05 500 60 60 1000 504. 39 202. 16 500 80 80 1000 498. 88 121. 47 500 100 1000 501. 72 91. 20 500 120 1000 498. 10 72. 01 500 140 1000 501. 14 58. 44 500 250 1000 498. 60 21. 72 500 500 1000 500. 00 • N = Total number of fish in the pond. • C = number of captured fish. • R = number of re-captured fish. • S = number of simulation with non-zero marked fish in recapture. Ka-fu Wong © 2003 17

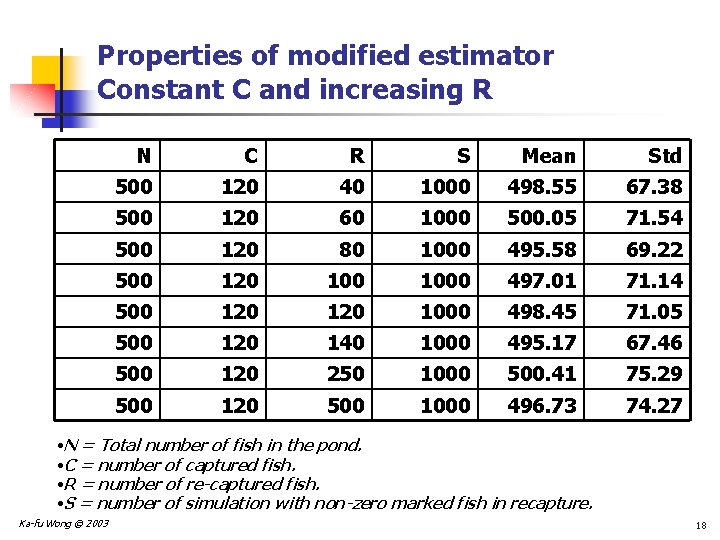
Properties of modified estimator Constant C and increasing R N C R S Mean Std 500 120 40 1000 498. 55 67. 38 500 120 60 1000 500. 05 71. 54 500 120 80 1000 495. 58 69. 22 500 120 1000 497. 01 71. 14 500 120 1000 498. 45 71. 05 500 120 140 1000 495. 17 67. 46 500 120 250 1000 500. 41 75. 29 500 120 500 1000 496. 73 74. 27 • N = Total number of fish in the pond. • C = number of captured fish. • R = number of re-captured fish. • S = number of simulation with non-zero marked fish in recapture. Ka-fu Wong © 2003 18

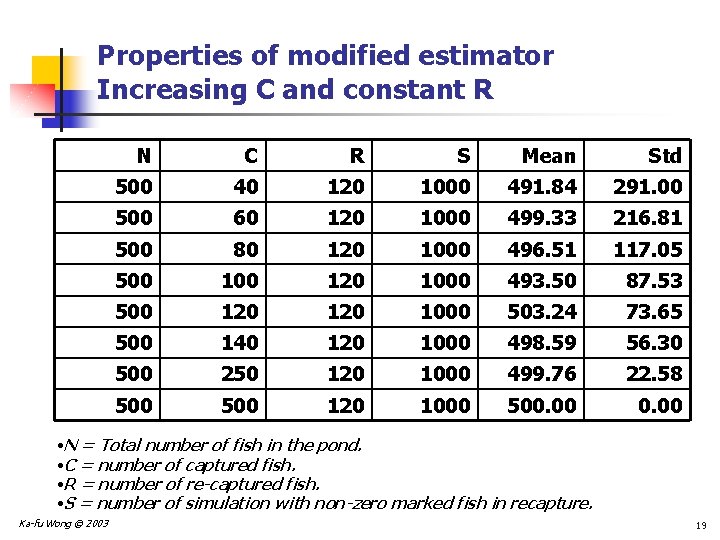
Properties of modified estimator Increasing C and constant R N C R S Mean Std 500 40 120 1000 491. 84 291. 00 500 60 120 1000 499. 33 216. 81 500 80 120 1000 496. 51 117. 05 500 120 1000 493. 50 87. 53 500 120 1000 503. 24 73. 65 500 140 120 1000 498. 59 56. 30 500 250 120 1000 499. 76 22. 58 500 120 1000 500. 00 • N = Total number of fish in the pond. • C = number of captured fish. • R = number of re-captured fish. • S = number of simulation with non-zero marked fish in recapture. Ka-fu Wong © 2003 19

Conclusion from the simulations n The modified estimator performs better than the original estimator. n There is no apparent bias. n The estimator is more precise. n Holding R constant, increasing the number of capture (C) helps: n The estimator is more precise, i. e. , standard deviation of the estimator is smaller. n Holding C constant, increasing the number of recapture (R) does not help: n The precision of the estimator is more or less unchanged. Ka-fu Wong © 2003 20

What to take away today n Statistics could be easy and intuitive. n Statistics need not be completely deep, murky, and mysterious. n Our common sense can help us to negotiate our way through the course. Syllabus will be distributed and discussed on Thursday 11 February 2003. Ka-fu Wong © 2003 21

In-class Lab Capture / recapture - END - Ka-fu Wong © 2003 Lab 1 -22
 Kafu wong
Kafu wong Kafu wong
Kafu wong Language
Language Kafu wong
Kafu wong Kafu wong
Kafu wong Dr colin wong
Dr colin wong Kafu wong
Kafu wong Epnp opencv
Epnp opencv Kafu wong
Kafu wong Kafu wong
Kafu wong Serat wulangreh kedadeyan saka ... pupuh
Serat wulangreh kedadeyan saka ... pupuh Marginal analysis econ
Marginal analysis econ Eg 1003
Eg 1003 Eg 1003 lab manual
Eg 1003 lab manual Eg.poly.nyu
Eg.poly.nyu Goetz 1003
Goetz 1003 Hoja de vida minerva 1003 resuelta
Hoja de vida minerva 1003 resuelta Manual.eg.poly
Manual.eg.poly 1001 1002 1003 1004
1001 1002 1003 1004 Tübitak 1004 bursiyer ücretleri
Tübitak 1004 bursiyer ücretleri Fig 1003
Fig 1003 Eg 1003
Eg 1003 Flv1003
Flv1003





































