DIMENZIONISANJE AKSIJALNO NAPREGNUTIH TAPOVA STEPEN SIGURNOSTI I DOZVOLJENI

DIMENZIONISANJE AKSIJALNO NAPREGNUTIH ŠTAPOVA. STEPEN SIGURNOSTI I DOZVOLJENI NAPON Osnovni zadatak proračuna elemenata konstrukcije vrši se tako da u uslovima eksploatacije oni budu pouzdani odnosno da pod dejstvom spoljašnjih sila se ne deformišu trajno ili da ne dodje do njihovog loma. Da ne bi došlo do ovih neželjenih posledica, naponi koji se javljaju u elementima konstrukcije moraju biti ispod kritičnih graničinih vrednosti. Maksimalni napon koji se nesme prekoračiti naziva se dozvoljenim naponom. Za aksijalno naprezanje u idelanom slučaju dozvoljeni napon iztezanja bio bi jednak ili manji od napona na granici proporcionalnosti. Pošto je za većinu materijala mnogo lakše i jednostavnije odrediti jačinu materijala pri kidanju nego napon na granici proporcionalnosti , dozvoljeni napon pri istezanju definiše se kao odnos količnika napona pri kidanju i stepena sigrunosti : gde je - stepen sigurnosti.

U zavisnosti od fizičko – mehaničkih karaktersitika materijala i vrste opterećenja stepen sigurnosti kreće se u intervalu vrednosti od 3 do 10. Kada je poznat dozvoljeni napon, onda se mogu postaviti statičke jednačine čvrstoće: , – dozvoljeni napon zatezanja. – dozvonjeni napon pritiska. ZATEZANJE ŠTAPA SOPSTVENOM TEŽINOM Neka je štap konstantne površine poprečnog preseka A uklješten na svom gornjem kraju (sl. 1), i on će se pod dejstvom sopstvene težine izdužiti za vrednost , gde je – specifična težina materijala. Da bi se odredilo izduženje štapa zamislimo da je štap presečen na udaljenju od tačke uklještenja i posmatrajmo ravnotežu odsečenog dela štapa. Uticaj odstranjenog dela štapa zamenjujemo unutrašnjim silama

koje moraju biti u ravnoteži sa težinom donjeg dela štapa Iz uslova ravnoteže: . dobijamo zakon raspodele normalnog napona u poprečnim presecima štapa: Iz prethodnog izraza se vidi da napon zavisi linearno od udaljenja (z) preseka. Poslednji izraz nam pokazuje da napon zavisi linearno od udaljenja (z) preseka. Maksimalna vrednost ovog napona je tj. i to je na mestu uklještenja. Ako je udaljenje onda će ovaj napon biti jednak nuli. Dijagram napona u ovom slučaju je prikazan na sledećoj slici 1.

Slika 1. Zatezanje štapa sopstvenom težinom Tamo gde je napon maksimalan a u ovom našem slučaju je to uklještenje štapa i to je najopterećeniji presek, pa se ovaj presek naziva opasnim presekom. Kidanje štapa nastupilo bi onda kada bi se napon usled sopstvene težine izjednačio sa težinom materijala na kidanje tj. pri čemu je - kritična dužina štapa pri kojoj bi nastalo kidanje štapa usled sopstvene težine štapa i izražava se kao:

Pošto se napon menja od najmanje vrednosti do najveće, to se dilatacija može izračunati sledećim izrazom: Ako u ovom izrazu uvedemo i težinu štapa pošto je: je izraz za dijelataciju: Na osnovu ovog izraza ukupna izduženja štapa iznosi: onda u kome je: – modul elastičnosti materijala štapa, – težina štapa, l – dužina štapa, A - površina poprečnog preseka štapa.

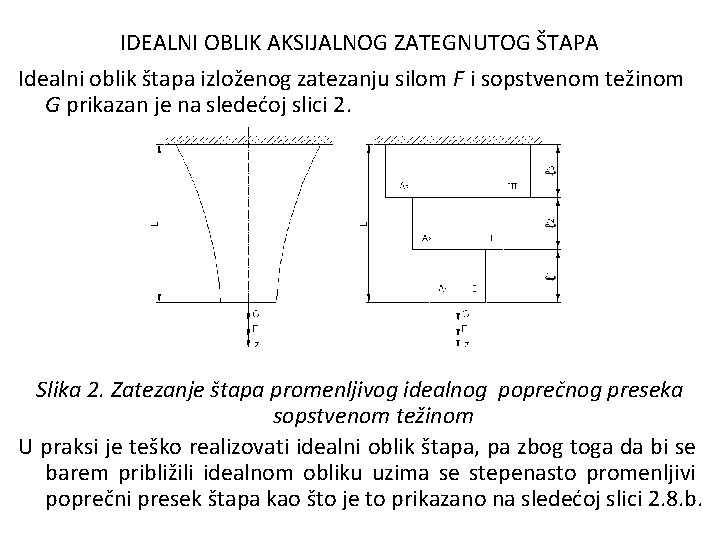
IDEALNI OBLIK AKSIJALNOG ZATEGNUTOG ŠTAPA Idealni oblik štapa izloženog zatezanju silom F i sopstvenom težinom G prikazan je na sledećoj slici 2. Slika 2. Zatezanje štapa promenljivog idealnog poprečnog preseka sopstvenom težinom U praksi je teško realizovati idealni oblik štapa, pa zbog toga da bi se barem približili idealnom obliku uzima se stepenasto promenljivi poprečni presek štapa kao što je to prikazano na sledećoj slici 2. 8. b.

• Idealni oblik štapa je jako teško realizovati u praksi, pa da bi se bar približili idealnom obliku, ide se sa stepenasto promenljivim poprečnim presekom, (sl. 2. 8. b). Proračun (dimenzionisanje) sprovodi se postupno primenom uslova ravnoteže na svaki deo štapa (stuba). • Proračun (dimenzionisanje) ovakvog oblika štapa sprovodi se postupno primenom uslova ravnoteže za svaki deo štapa (stub I, III) (slika 3. ). Slika 3. Opterećenje stepenasto promenljivog poprečnog preseka

Uslov ravnoteže prvog dela štapa (stub I) sledi (slika 3. a): Uslov ravnoteže drugog dela štapa (stub II) sledi (slika 3. b): Za treći deo štapa (stub III) takođe na isti način kao i prethodni, dobija se površina poprečnog preseka u obliku: Na isti način postupa se i za ostale delove štapa, za svaki deo posmatra se njegova ravnoteža usled dejstva sila koje deluju na njega, pa je za n-ti deo štapa:

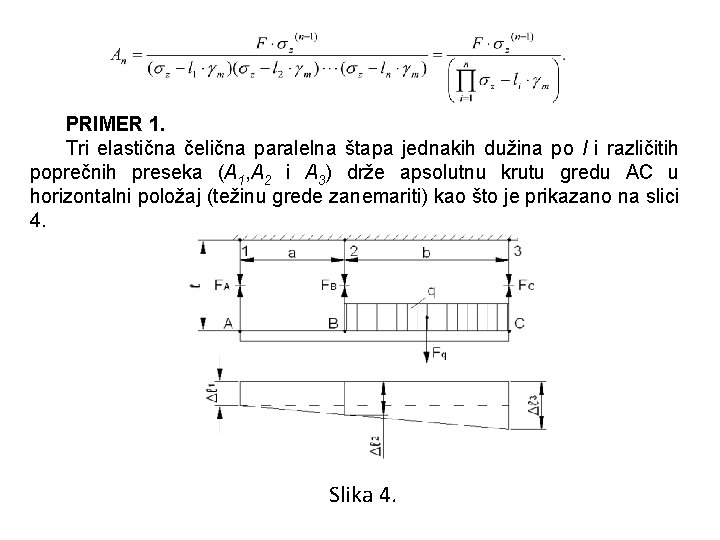
PRIMER 1. Tri elastična čelična paralelna štapa jednakih dužina po l i različitih poprečnih preseka (A 1, A 2 i A 3) drže apsolutnu krutu gredu AC u horizontalni položaj (težinu grede zanemariti) kao što je prikazano na slici 4. Slika 4.

• REŠENJE: U zadatku se javlja sistem od tri paralelne sile F 1, F 2 i F 3. Primenom statičkih uslova ravnoteže mogu se formirati dve jednačine , što znači da je sistem jedanput statički neodređen, pa je potrebno formirati još jednu dopunsku jednačinu. Iz statičkih uslova ravnoteže sledi: 1. 2. Na osnovu plana pomeranja datog na slici 4. sledi sličnost trouglova, odakle sledi relacija: , kao dopunski uslov koji ovaj slučaj svodi na statički određeni slučaj.

Kako je to se zamenom njihovih vrednosti u prethodni izraz dobija treća dopunska jednačina: 3. . Na ovaj način formirane su tri jednačine sa tri nepoznate (sile u štapovima F 1, F 2 i F 3). Ako se uzme u obzir zadati uslov A 1= A 2 = A i b = 2 a, intenziteti ovih sila iznose: PRIMER 2. Betonski zid sastavljen je iz 3 segmenata stepenika – stuba različitih visina i širina (prikazan na slici 5. ). Odrediti koliku silu stub može preneti kao i širine stepenika BC pod uslovom da je normalan napon u svim presecima (l-l); (2 -2); (3 -3) isti i iznosi a visine stepenika iznose: Širina prvog stepenika iznosi.

REŠENJE: Posmatraćemo zid dužine od stepenika iznosi: , pa površina prvog Sila pritiska F na zid može se odrediti iz uslova ravnoteže prvog segmenta stuba: odakle je: gde je . Sl. 5.

Iz odgovarajućih jednačina ravnoteže stuba može se odrediti površina drugog i trećeg stepenika: Širina drugog i trećeg stepenika stuba iznose:

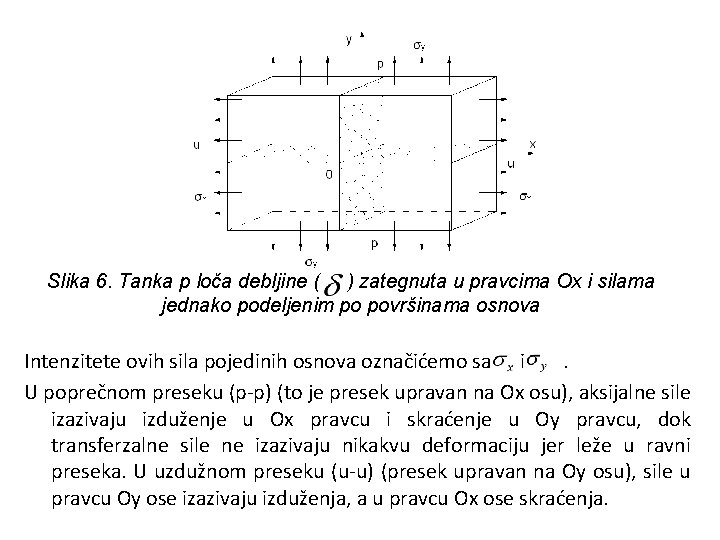
NAPREZANJE U DVA PRAVCA ZATEZANJE U DVA UPRAVNA PRAVCA NAPREZANJE U DVA UPRAVNA PRAVCA • Često se u praksi događa da su elementi konstrukcije opterećeni sistemom spoljašnjih sila tako da se u njima pojavljuju naponi u dva međusobno upravna pravca. • Mnoge konstrukcije kao svoje sastavne elemente imaju tanke ploče koje su opterećene u pravcu svoje srednje površine. • Ovi elementi su male debljine pa se za njih može uvesti pretpostavka o ravnomernoj raspodeli napona po debljini, na taj način problem u osnovi prostora može se svesti na ravanski. • Neka je tanka ploča debljine ( ), (sl. 6. ) zategnuta u pravcima Ox i Oy (ose ravanskog koordinatnog sistema) silama jednako podeljenim po površinama osnova.

Slika 6. Tanka p loča debljine ( ) zategnuta u pravcima Ox i silama jednako podeljenim po površinama osnova Intenzitete ovih sila pojedinih osnova označićemo sa i. U poprečnom preseku (p-p) (to je presek upravan na Ox osu), aksijalne sile izazivaju izduženje u Ox pravcu i skraćenje u Oy pravcu, dok transferzalne sile ne izazivaju nikakvu deformaciju jer leže u ravni preseka. U uzdužnom preseku (u-u) (presek upravan na Oy osu), sile u pravcu Oy ose izazivaju izduženja, a u pravcu Ox ose skraćenja.

Usled dejstva ovih sila u poprečnim presecima javljaju se normalni naponi a uzdužnim presecima. Naponu odgovara pozitivna uzdužna dilatacija i negativna poprečna dilatacija u pravcu. S obzirom na izraze ( ), uzdužne i poprečne dilatacije u pravcu koordinatnih osa iznose (tabela 1. ): (ukupne dilatacije) u pravcu koordinatnih osa Ox i Oy Iz prethodnih izraza mogu se odrediti normalni naponi u zavisnosti od dilatacija primenom :

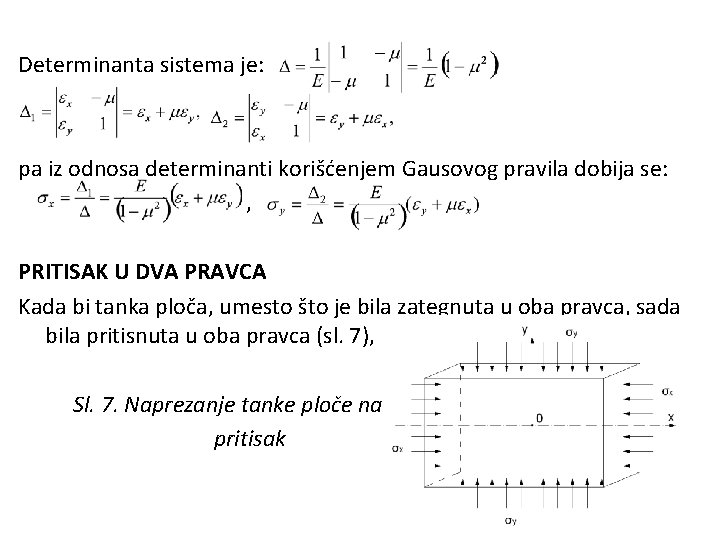
Determinanta sistema je: pa iz odnosa determinanti korišćenjem Gausovog pravila dobija se: , PRITISAK U DVA PRAVCA Kada bi tanka ploča, umesto što je bila zategnuta u oba pravca, sada bila pritisnuta u oba pravca (sl. 7), Sl. 7. Naprezanje tanke ploče na pritisak

sličnom analizom kao i za prethodni slučaj dobijaju se dilatacije u pravcu koordinatnih osa prikazane u tabeli 2. (ukupne dilatacije) u pravcu koordinatnih osa Ox i Oy Ukupne dilatacije iznose: Dilatacije su, po apsolutnoj vrednosti, iste kao i kod tanke ploče zategnute u dva pravca, samo su negativnog predznaka.

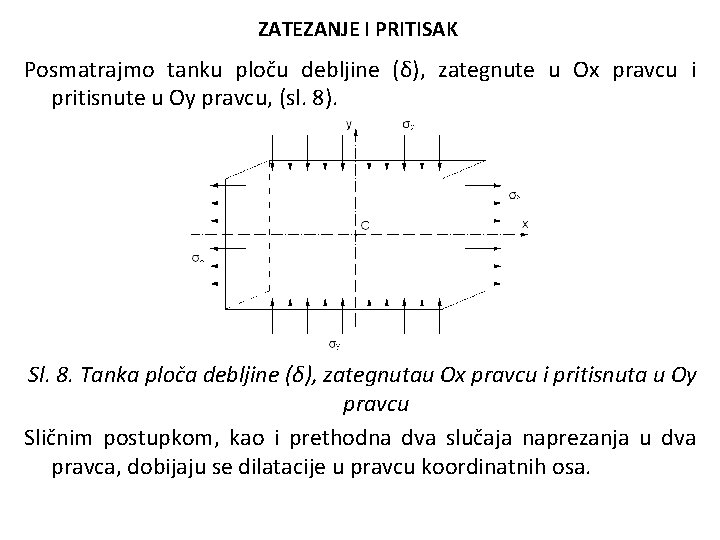
ZATEZANJE I PRITISAK Posmatrajmo tanku ploču debljine (δ), zategnute u Ox pravcu i pritisnute u Oy pravcu, (sl. 8). Sl. 8. Tanka ploča debljine (δ), zategnutau Ox pravcu i pritisnuta u Oy pravcu Sličnim postupkom, kao i prethodna dva slučaja naprezanja u dva pravca, dobijaju se dilatacije u pravcu koordinatnih osa.

Ukupne dilatacije onda iznose: PRIMER 3. Tanka pravougaona ploča debljine , širine i visine h=60 mm zategnuta je u pravcu x – ose silom Fx=24 KN a u pravcu y – ose silom Fy= 30 KN , (sl. 9). Odrediti napone u poprečnim presecima i dilatacije u pravcu koordinatnih osa, ako je modul elastičnosti materijala , a Poasonov koeficijent REŠENJE. Površine poprečnih preseka iznose:

Normalni naponi u poprečnim presecima su: Dilatacije u pravcu koordinatnih osa iznose: