Developing Formulas for Developing Formulas 9 2 Circles






























- Slides: 31

Developing Formulas for Developing Formulas 9 -2 Circles and Regular Polygons Warm Up Lesson Presentation Lesson Quiz Holt Geometry

9 -2 Developing Formulas for Circles and Regular Polygons Warm Up Find the unknown side lengths in each special right triangle. 1. a 30°-60°-90° triangle with hypotenuse 2 ft 2. a 45°-90° triangle with leg length 4 in. 3. a 30°-60°-90° triangle with longer leg length 3 m Holt Geometry

9 -2 Developing Formulas for Circles and Regular Polygons Objectives Develop and apply the formulas for the area and circumference of a circle. Develop and apply the formula for the area of a regular polygon. Holt Geometry

9 -2 Developing Formulas for Circles and Regular Polygons Vocabulary circle center of a regular polygon apothem central angle of a regular polygon Holt Geometry

9 -2 Developing Formulas for Circles and Regular Polygons A circle is the locus of points in a plane that are a fixed distance from a point called the center of the circle. A circle is named by the symbol and its center. A has radius r = AB and diameter d = CD. The irrational number is defined as the ratio of the circumference C to the diameter d, or Solving for C gives the formula C = d. Also d = 2 r, so C = 2 r. Holt Geometry

9 -2 Developing Formulas for Circles and Regular Polygons You can use the circumference of a circle to find its area. Divide the circle and rearrange the pieces to make a shape that resembles a parallelogram. The base of the parallelogram is about half the circumference, or r, and the height is close to the radius r. So A r · r = r 2. The more pieces you divide the circle into, the more accurate the estimate will be. Holt Geometry

9 -2 Developing Formulas for Circles and Regular Polygons Holt Geometry

9 -2 Developing Formulas for Circles and Regular Polygons Example 1 A: Finding Measurements of Circles Find the area of K in terms of . Holt Geometry A = r 2 Area of a circle. A = (3)2 Divide the diameter by 2 to find the radius, 3. A = 9 in 2 Simplify.

9 -2 Developing Formulas for Circles and Regular Polygons Example 1 B: Finding Measurements of Circles Find the radius of J if the circumference is (65 x + 14) m. C = 2 r (65 x + 14) = 2 r Circumference of a circle Substitute (65 x + 14) for C. r = (32. 5 x + 7) m Divide both sides by 2. Holt Geometry

9 -2 Developing Formulas for Circles and Regular Polygons Example 1 C: Finding Measurements of Circles Find the circumference of M if the area is 25 x 2 ft 2 Step 1 Use the given area to solve for r. A = r 2 Holt Geometry Area of a circle 25 x 2 = r 2 Substitute 25 x 2 for A. 25 x 2 = r 2 Divide both sides by . 5 x = r Take the square root of both sides.

9 -2 Developing Formulas for Circles and Regular Polygons Example 1 C Continued Step 2 Use the value of r to find the circumference. C = 2 r Holt Geometry C = 2 (5 x) Substitute 5 x for r. C = 10 x ft Simplify.

9 -2 Developing Formulas for Circles and Regular Polygons Check It Out! Example 1 Find the area of A in terms of in which C = (4 x – 6) m. A = r 2 A = (2 x – Area of a circle. 3)2 m Divide the diameter by 2 to find the radius, 2 x – 3. A = (4 x 2 – 12 x + 9) m 2 Simplify. Holt Geometry

9 -2 Developing Formulas for Circles and Regular Polygons Helpful Hint The key gives the best possible approximation for on your calculator. Always wait until the last step to round. Holt Geometry

9 -2 Developing Formulas for Circles and Regular Polygons Example 2: Cooking Application A pizza-making kit contains three circular baking stones with diameters 24 cm, 36 cm, and 48 cm. Find the area of each stone. Round to the nearest tenth. 24 cm diameter A = (12)2 ≈ 452. 4 cm 2 Holt Geometry 36 cm diameter A = (18)2 ≈ 1017. 9 cm 2 48 cm diameter A = (24)2 ≈ 1809. 6 cm 2

9 -2 Developing Formulas for Circles and Regular Polygons Check It Out! Example 2 A drum kit contains three drums with diameters of 10 in. , 12 in. , and 14 in. Find the circumference of each drum. 10 in. diameter 12 in. diameter 14 in. diameter C = d C = (10) C = (12) C = (14) C = 31. 4 in. C = 37. 7 in. C = 44. 0 in. Holt Geometry

9 -2 Developing Formulas for Circles and Regular Polygons The center of a regular polygon is equidistant from the vertices. The apothem is the distance from the center to a side. A central angle of a regular polygon has its vertex at the center, and its sides pass through consecutive vertices. Each central angle measure of a regular n-gon is Holt Geometry

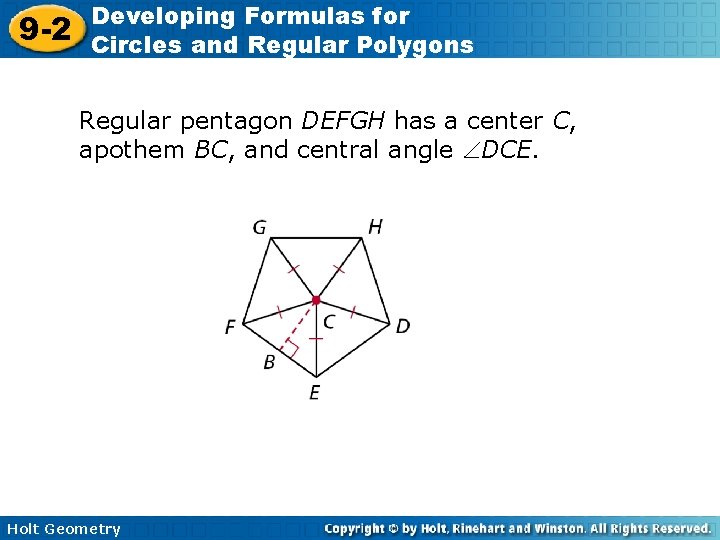
9 -2 Developing Formulas for Circles and Regular Polygons Regular pentagon DEFGH has a center C, apothem BC, and central angle DCE. Holt Geometry

9 -2 Developing Formulas for Circles and Regular Polygons To find the area of a regular n-gon with side length s and apothem a, divide it into n congruent isosceles triangles. area of each triangle: total area of the polygon: The perimeter is P = ns. Holt Geometry

9 -2 Developing Formulas for Circles and Regular Polygons Holt Geometry

9 -2 Developing Formulas for Circles and Regular Polygons Example 3 A: Finding the Area of a Regular Polygon Find the area of regular heptagon with side length 2 ft to the nearest tenth. Step 1 Draw the heptagon. Draw an isosceles triangle with its vertex at the center of the heptagon. The central angle is . Draw a segment that bisects the central angle and the side of the polygon to form a right triangle. Holt Geometry

9 -2 Developing Formulas for Circles and Regular Polygons Example 3 A Continued Step 2 Use the tangent ratio to find the apothem. The tangent of an angle is opp. leg. adj. leg Solve for a. Holt Geometry

9 -2 Developing Formulas for Circles and Regular Polygons Example 3 A Continued Step 3 Use the apothem and the given side length to find the area. Area of a regular polygon The perimeter is 2(7) = 14 ft. A 14. 5 ft 2 Holt Geometry Simplify. Round to the nearest tenth.

9 -2 Developing Formulas for Circles and Regular Polygons Remember! The tangent of an angle in a right triangle is the ratio of the opposite leg length to the adjacent leg length. See page 525. Holt Geometry

9 -2 Developing Formulas for Circles and Regular Polygons Example 3 B: Finding the Area of a Regular Polygon Find the area of a regular dodecagon with side length 5 cm to the nearest tenth. Step 1 Draw the dodecagon. Draw an isosceles triangle with its vertex at the center of the dodecagon. The central angle is . Draw a segment that bisects the central angle and the side of the polygon to form a right triangle. Holt Geometry

9 -2 Developing Formulas for Circles and Regular Polygons Example 3 B Continued Step 2 Use the tangent ratio to find the apothem. The tangent of an angle is Solve for a. Holt Geometry opp. leg. adj. leg

9 -2 Developing Formulas for Circles and Regular Polygons Example 3 B Continued Step 3 Use the apothem and the given side length to find the area. Area of a regular polygon The perimeter is 5(12) = 60 ft. A 279. 9 cm 2 Holt Geometry Simplify. Round to the nearest tenth.

9 -2 Developing Formulas for Circles and Regular Polygons Check It Out! Example 3 Find the area of a regular octagon with a side length of 4 cm. Step 1 Draw the octagon. Draw an isosceles triangle with its vertex at the center of the octagon. The central angle is . Draw a segment that bisects the central angle and the side of the polygon to form a right triangle. Holt Geometry

9 -2 Developing Formulas for Circles and Regular Polygons Check It Out! Example 3 Continued Step 2 Use the tangent ratio to find the apothem The tangent of an angle is opp. leg. adj. leg Solve for a. Holt Geometry

9 -2 Developing Formulas for Circles and Regular Polygons Check It Out! Example 3 Continued Step 3 Use the apothem and the given side length to find the area. Area of a regular polygon The perimeter is 4(8) = 32 cm. A ≈ 77. 3 cm 2 Holt Geometry Simplify. Round to the nearest tenth.

9 -2 Developing Formulas for Circles and Regular Polygons Lesson Quiz: Part I Find each measurement. 1. the area of D in terms of A = 49 ft 2 2. the circumference of T in which A = 16 mm 2 C = 8 mm Holt Geometry

9 -2 Developing Formulas for Circles and Regular Polygons Lesson Quiz: Part II Find each measurement. 3. Speakers come in diameters of 4 in. , 9 in. , and 16 in. Find the area of each speaker to the nearest tenth. A 1 ≈ 12. 6 in 2 ; A 2 ≈ 63. 6 in 2 ; A 3 ≈ 201. 1 in 2 Find the area of each regular polygon to the nearest tenth. 4. a regular nonagon with side length 8 cm A ≈ 395. 6 cm 2 5. a regular octagon with side length 9 ft A ≈ 391. 1 ft 2 Holt Geometry
 Developing formulas for circles and regular polygons
Developing formulas for circles and regular polygons 10-2 developing formulas for circles and regular polygons
10-2 developing formulas for circles and regular polygons 10-2 developing formulas for circles and regular polygons
10-2 developing formulas for circles and regular polygons Developing formulas for circles and regular polygons
Developing formulas for circles and regular polygons 9-2 developing formulas for circles and regular polygons
9-2 developing formulas for circles and regular polygons Area of polygons and circles
Area of polygons and circles Segment lengths in circles formulas
Segment lengths in circles formulas Angles in circles formulas
Angles in circles formulas Segment lengths intersecting chords secants and tangents
Segment lengths intersecting chords secants and tangents Developing formulas for triangles and quadrilaterals
Developing formulas for triangles and quadrilaterals Developing formulas for triangles and quadrilaterals
Developing formulas for triangles and quadrilaterals Developing formulas for triangles and quadrilaterals
Developing formulas for triangles and quadrilaterals Developing formulas for triangles and quadrilaterals
Developing formulas for triangles and quadrilaterals Shaktismen
Shaktismen Centrum för kunskap och säkerhet
Centrum för kunskap och säkerhet Jag har gått inunder stjärnor text
Jag har gått inunder stjärnor text Inköpsprocessen steg för steg
Inköpsprocessen steg för steg Påbyggnader för flakfordon
Påbyggnader för flakfordon Strategi för svensk viltförvaltning
Strategi för svensk viltförvaltning Anatomi organ reproduksi
Anatomi organ reproduksi Egg för emanuel
Egg för emanuel Hur räknar man standardavvikelse
Hur räknar man standardavvikelse Rutin för avvikelsehantering
Rutin för avvikelsehantering Tack för att ni har lyssnat
Tack för att ni har lyssnat Läkarutlåtande för livränta
Läkarutlåtande för livränta Formuö
Formuö Klassificeringsstruktur för kommunala verksamheter
Klassificeringsstruktur för kommunala verksamheter Myndigheten för delaktighet
Myndigheten för delaktighet Debatt mall
Debatt mall Tack för att ni lyssnade
Tack för att ni lyssnade En lathund för arbete med kontinuitetshantering
En lathund för arbete med kontinuitetshantering Tobinskatten för och nackdelar
Tobinskatten för och nackdelar